Flow in a 3D diffuser

Computational Details

This section provides details of the computational strategies employed to compute the present case. Firstly, details of the numerical solver are given. Then, information about the computational grid is provided. Finally, the statistical quantities and their computation are explained.

Computational approach

Alya is a parallel multi-physics/multiscale simulation code developed at the Barcelona Supercomputing Centre to run efficiently on high-performance computing environments. For this DNS, the data has been obtained using the incompressible Navier-Stokes solver of Alya since the flow is not subject to compressibility effects. The general code is described in Vazquezet al. (2016) while the latest numerical schemes for the incompressible flow solver are described in Lehmkuhl et al. (2019).

In a nutshell, the convective term is discretized using a Galerkin finite element (FEM) scheme recently proposed by Charnyi et al. (2017), which conserves linear and angular momentum, and kinetic energy at the discrete level (see Olshanskii and Rebholz (2020)). Neither upwinding nor any equivalent momentum stabilization is employed. In order to use equalorder elements, numerical dissipation is introduced only for the pressure stabilization via a fractional step scheme (Codina (2001)), which is similar to the approach for the pressure-velocity coupling in unstructured, collocated finite-volume codes (see, for example, Jofre et al. (2014)). The set of equations is integrated in time using a third order Runge-Kutta explicit method (see Capuano et al. (2017)) combined with an eigenvalue-based time-step estimator (see Trias and Lehmkuhl (2011)). This approach has been shown to be significantly less dissipative than the traditional stabilized FEM approach (see Lehmkuhl et al. (2019)). Thus, is an optimal methodology for high-fidelity simulations of complex flows as the ones required in the present project.

Spatial and temporal resolution, grids

The computational grid resulted in about 250 million elements and approximately 1,000 million degrees of freedom (DoF). Details of the computational grid are provided in Fig. 8 and Fig. 9. With a stretched grid, the maximum grid resolution in the duct centre is ${\Delta z^{+}=11.6}$ , ${\Delta y^{+}=13.2}$ , ${\Delta x^{+}=19.5}$ . At the wall (in terms of the first grid point), the resolution is ${z^{+}=0.074}$ , ${y^{+}=0.37}$ in the spanwise and normal directions, respectively. For the temporal integration, a third order explicit Runge Kutta scheme was used with a dynamic time stepping that ensured a CFL below 0.9. The flow was computed for ${t=U_{\textrm {bulk}}/L=13}$ flow-through times based on the duct length before gathering statistics for and additional ${t=U_{\textrm {bulk}}/L=21}$ flow-through times. This setup was deemed sufficient to compute the flow in the diffuser and is based on the previous DNS of Ohlsson et al. (2010).

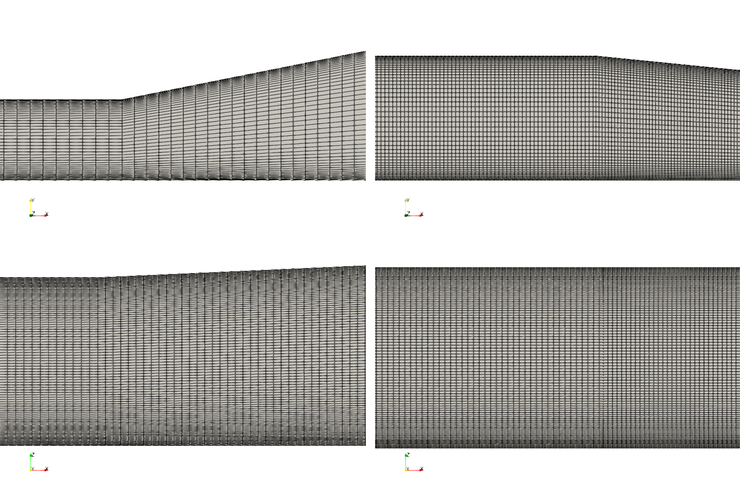
Figure 8: Details of the computational mesh. XY (top) and XZ (bottom) plane views in the entrance (left) and mid (right) sections of the diffuser. Only every 4th grid line is shown.

Figure 9: Details of the computational mesh in various cross-sections corresponding to: inlet duct (top left), diffuser expansion (top right), diffuser mid section (bottom left) and diffuser exit (bottom right). Only every 4th grid line is shown.

Solution smoothing

Given the presence of high frequency noise in the DNS solution, a smoothing procedure has been applied to the results. This smoothing is only applied when explicitly indicated (Figs. 20 to 23), otherwise the raw data is provided. Smoothing is only applied to the final fields, i.e., after all the computations are already finished, and as a previous step before plotting.

The smoothing procedure used is intrinsic to the finite-element machinery used to obtain the solution. The procedure basically consists of interpolating the solution from the nodal elements to the Gauss points and projecting it back to the nodes. Both interpolations use the shape functions of the element so that a second order accuracy is achieved (for the kind of elements used in this solution). The procedure is inherent to finite elements in the sense that the fields are brought to the Gauss points (e.g., to compute gradients) and then after the necessary computations put back to the nodes (e.g., projecting the gradient obtained at the Gauss points to the nodes for future calculations).

Doing this procedure iteratively is similar to applying a Gaussian filter to the solution field, filtering out the high frequency oscillations. The aggressiveness of this smoothing is controlled by the number of times the projection to the Gauss nodes and back is done. For the present results, a total number of five iterations has been deemed enough (so as not to damage the signal and have an effect on the physics of the problem).

Computation of statistical quantities

The statistical quantities are computed a posteriori from the velocity and pressure fields gathered during an additional 21 flowthrough-times. In a first step, the time-averaged pressure and velocity fields are gathered among 1881 snapshots. These snapshots are considered to be loosely correlated (i.e., as independent experiments) hence a simple average is performed. Afterwards, the time-averaged pressure and velocity gradients are computed from the time-averaged pressure and velocity fields.

Then, the fluctuating quantities are obtained as:

Fluctuating pressure ${p=P-{\overline {P}}}$
Fluctuating velocity ${u=U-{\overline {U}}}$

along with their gradients as:

Gradient of fluctuating pressure ${p_{,k}=P_{,k}-{\overline {P}}_{,k}}$
Gradient of fluctuating velocity ${u_{,k}=U_{,k}-{\overline {U}}_{,k}}$

Using these quantities, the Reynolds stress tensor is easily recovered, along with the pressure autocorrelation, pressure-velocity correlation and triple velocity correlation:

Reynolds stresses ${R_{ij}^{*}=\rho {\overline {u_{i}u_{j}}}}$
Pressure autocorrelation ${\overline {pp}}$
Pressure velocity correlation ${\overline {pu_{i}}}$
Triple velocity correlation ${\rho {\overline {u_{i}u_{j}u_{k}}}}$

The Reynolds stress budget equation terms are recovered using the aforementioned quantities and their gradients using matrix and vectorial math:

Convection ${C_{ij}^{*}=(R_{ij}^{*}{\overline {u}}_{k})_{,k}}$
Production ${P_{ij}^{*}=-(R_{ik}^{*}{\overline {u}}_{j,k}+R_{jk}^{*}{\overline {u}}_{i,k})}$
Turbulent diffusion ${D_{ij}^{1*}=-\rho ({\overline {u_{i}u_{j}u_{k}}})_{,k}}$
Pressure diffusion ${D_{ij}^{2*}=-\rho ({\overline {p(u_{i}\delta _{jk}+u_{j}\delta _{ik})}})_{,k}}$
Viscous diffusion ${D_{ij}^{3*}=\mu ({\overline {u_{i}u_{j}}})_{,kk}}$
Pressure strain ${\Phi _{ij}^{*}={\overline {p(u_{i,j}+u_{j,i})}}}$
Dissipation ${\epsilon _{ij}^{*}=2\mu {\overline {u_{i,j}u_{j,k}}}}$

Finally, Taylor lengthscale and Kolmogorov length and time scales are recovered as:

Taylor microscale ${\eta _{T}={\sqrt {\left|10\nu {\frac {k}{\varepsilon +s}}\right|}}}$
Kolmogorov length scale ${\eta _{K}=\left|{\frac {\nu ^{3}}{\varepsilon +s}}\right|^{0.25}}$
Kolmogorov time scale ${\tau _{K}={\sqrt {\left|{\frac {\nu }{\varepsilon +s}}\right|}}}$

Where ${\varepsilon }$ stands for the dissipation in the budget equation for the turbulent kinetic energy ${k}$ . The absolute value is taken to avoid negative roots and ${s}$ is a small value to avoid numerically dividing by zero. For a more in-detailed explanation on how these quantities have been obtained, the reader is referred to this document (PDF).

References

Charnyi, S., Heister, T., Olshanskii, M. A. and Rebholz, L. G. (2017): On conservation laws of NavierStokes Galerkin discretizations. In Journal of Computational Physics, Vol. 337, pp. 289-308.
Jofre, L., Lehmkuhl, O., Ventosa, J., Trias, F. and Oliva, A. (2014): Conservation properties of unstructured finite-volume mesh schemes for the Navier-Stokes equations. In Numerical Heat Transfer, Part B: Fundamentals, Vol. 54, no. 1, pp. 289-308.
Codina, R. (2001): Pressure stability in fractional step finite element methods for incompressible flows. In Journal of Computational Physics, Vol. 170, no. 1, pp. 112-140.
Trias, F. X. and Lehmkuhl, O. (2011): A self-adaptive strategy for the time integration of NavierStokes equations. In Numerical Heat Transfer. Part B, Vol. 60, no. 2, pp. 116-134.
Lehmkuhl, O., Houzeaux, G., Owen, H., Chrysokentis, G. and Rodriguez, I. (2019): A low-dissipation finite element scheme for scale resolving simulations of turbulent flows. In Journal of Computational Physics, Vol. 390, pp. 51-65.
Vázquez, M., Houzeaux, G., Koric, S., Artigues, A., Aguado-Sierra, J., Arís, R., Mira, D., Calmet, H., Cucchietti, F., Owen, H., Taha, A., Burness, E. D., Cela, J. M., & Valero, M. (2016): Alya: Multiphysics engineering simulation toward exascale. In Journal of Computational Science, Vol. 14, pp. 15-27.
Olshanskii, M. A., & Rebholz, L. G. (2020): Longer time accuracy for incompressible Navier–Stokes simulations with the EMAC formulation. In Computer Methods in Applied Mechanics and Engineering, Vol. 372, pp. 113369.
Capuano, F., Coppola, G., Rández, L., & Luca, L. De (2017): Explicit Runge – Kutta schemes for incompressible flow with improved energy-conservation properties. In Journal of Computational Physics, Vol. 328, pp. 86–94.