DNS 1-3
Flow in a 3D diffuser
Abstract
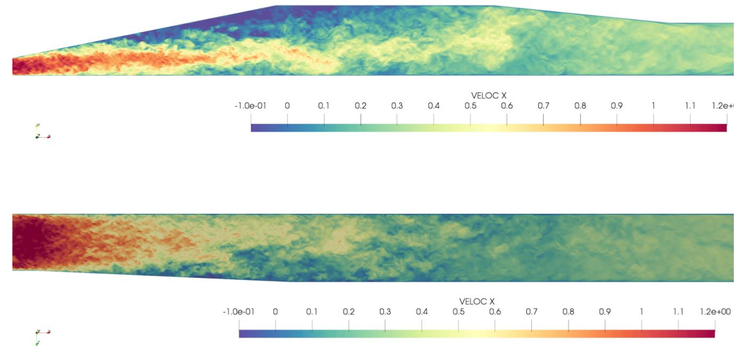
The 3D (Stanford) Diffuser is identified as a case with complex internal corner flow and 3D separation, is well documented (see, e.g., UFR_4-16_Test_Case) and has a relatively simple geometry. The diffuser has an inlet section, an expansion section and an outlet section (see Figure 1). The flow at the inlet is assumed to be a fully developed rectangular channel flow. At the outlet, standard Dirichlet condition for the pressure is prescribed. An inflow Reynolds number of 10000 is considered based on the duct height and bulk velocity. The flow is considered to be incompressible.
This test case concerns a highly resolved Direct Numerical Simulation (DNS) using the in-house Finite Element Method (FEM) code Alya developed at BSC. The parallel multi-physics code Alya has been designed for large-scale parallel applications and uses a non-incremental fractional-step method to stabilize pressure, with an explicit fourth-order Runge-Kutta time integration scheme. The final scheme preserves momentum, angular momentum and kinetic energy at the discrete level.
The primary objective of this contribution is to provide a rich database of flow and turbulence statistics for verification and validation on subsequent computational campaigns. The provided statistical quantities in the database are:
- mean pressure and velocities;
- Reynolds stress components;
- pressure autocorrelation;
- Taylor microscale;
- Kolmogorov length and time scales;
The following quantities are provided for the inlet duct section only:
- Reynolds stress equations budget terms;
- triple velocity correlation;
- pressure-velocity correlation.
© copyright ERCOFTAC 2024