UFR 4-20 Description
Mixing ventilation flow in an enclosure driven by a transitional wall jet
Confined Flows
Underlying Flow Regime 4-20
Description
Introduction
Ventilation flow is important for creating a healthy, comfortable, sustainable and energy-efficient indoor climate in buildings and other enclosures, such as airplanes, cars, ships, and a correct understanding of ventilation flows is therefore of large importance. Two important assessment methods that can be used to obtain detailed information on ventilation flows are experiments, either reduced-scale or full-scale, and computational fluid dynamics (CFD) simulations. The use of CFD to assess ventilation flows in building has strongly increased since the early work by Nielsen in the 1970s (Nielsen, 1974). Nowadays, it is a primary method for the detailed assessment of indoor airflow in buildings and other enclosures in the design phase or to optimize ventilation in existing buildings (e.g. Chen 1995, 1996, 2009; Nielsen 1998; Jiang and Chen 2002; Heiselberg et al. 2004; Wright and Hargreaves 2006; Hu et al. 2008; Norton et al. 2009; van Hooff and Blocken 2010a,b; Li and Nielsen 2011; Ramponi and Blocken 2012). CFD model validation should ensure a proper representation of the reality by the used CFD model (Casey and Wintergerste 2000) and requires detailed and well-described experiments. In this UFR, reduced-scale experiments are presented alongside CFD simulations. Although reduced-scale experiments can suffer from scaling problems; i.e. combined modeling of inertial and buoyancy forces (if present), they can also be advantageous due to the potential lower costs and the more straightforward application of particle image velocimetry (PIV), which can provide detailed overall information on the ventilation flow field in a 2D plane.
This UFR focuses on a generic mixing ventilation case for transitional slot Reynolds numbers in a cubical enclosure (Fig. 1). Mixing ventilation consists of the injection of an air jet in the upper part of the room (e.g. Etheridge and Sandberg 1996; Awbi 2007). The jet momentum should ensure mixing of the fresh supply air with the room air, after which the diluted air should be extracted from the room. Attachment of the jet to the ceiling, also known as the ‘Coanda effect’, is used to ensure that the supply air jet does not penetrate the occupied zone too early and helps preventing draught problems in the enclosure (e.g. Awbi 2003, 2007). Although several experimental studies have been performed in various geometries in the past to analyze mixing ventilation flow problems, the majority of these studies focused on mixing ventilation flows within the fully turbulent regime, i.e. for high slot Reynolds numbers (Re) (e.g. Nielsen 1990; Chen 1995,1996; Nielsen 1998; Zhang et al. 2000), which can be defined as with the characteristic inlet velocity (m/s), the supply slot height (m) and the kinematic viscosity (m2/s). Low values of Re can indicate the presence of a transitional flow regime inside the room, which can be distinguished from turbulent flow by the presence of relatively large and persistent coherent structures (vortices), caused by Kelvin-Helmholtz type instabilities in the shear layer of the jet. Mixing ventilation flows driven by transitional plane wall jets have not been studied often in the past.
This UFR focuses on the modeling of mixing ventilation flow driven by a transitional wall jet in a generic cubical enclosure (Fig. 1). This UFR is of special relevance to UFR 4-11, and indirectly to AC 4-03.
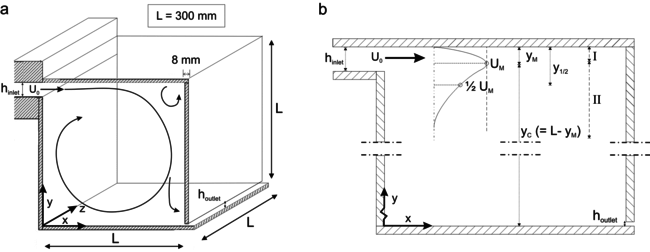
|
| Figure 1: (a) 3D room geometry with indication of coordinate system, U0, hinlet, houtlet, and dimensions of the test section L3. (b) 2D schematic representation of the plane wall jet with I the inner region, II the outer region, UM the maximum velocity, yM the distance from the top wall to the location of UM, yC the distance from the bottom wall to the location of UM and y½ the location of ½ UM in the outer region (e.g. Launder and Rodi 1981). Figure from van Hooff et al. (2012a). |
Review of UFR studies and choice of test case
In the past, several publications indicated that transitional flow can be present in different types of room airflow, e.g. in the supply jet region, corners of the room, or in the vicinity of buoyant plumes (e.g.
Topp et al. 2000;
Davidson et al. 2000;
Sørensen and Nielsen 2003;
Wang and Chen 2009, 2010;
Li and Nielsen 2011).
Although the possibility of transitional ventilation flow has been indicated in the aforementioned studies, the importance of transitional ventilation flows in general, and the modeling of transitional ventilation flows in rooms or other enclosures has only been addressed in a very limited number of publications so far.
Nielsen et al. (2000),
Topp et al. (2000)
and
Davidson et al. (2000)
performed measurements and CFD simulations of forced mixing ventilation at transitional slot Reynolds numbers. Hot-sphere anemometers were used to measure room airflow resulting from a plane low-Re wall jet (Re ≈ 79-770). The enclosure was 4.2 m deep and the inlet height was 0.02 m. They concluded that the velocity profiles fitted neither a laminar nor a turbulent relation and therefore concluded that the flow was transitional.
In addition, some other studies have been published on transitional wall jets, e.g.
Bajura and Catalano (1975),
Lichter et al. (1992),
Hsiao and Sheu (1994),
Gogineni and Shih (1997),
however, these studies did not focus on confined flows as present in mixing ventilation cases and therefore had a different focus and a different flow pattern.
In addition to the lack of experimental data on mixing ventilation driven by transitional wall jets, there is no consensus in literature on the capability of steady Reynolds-averaged Navier-Stokes (RANS) models to accurately predict time-averaged transitional flows in mixing ventilation cases.
The next sections focus on the assessment of the accuracy of steady RANS CFD in combination with three frequently used turbulence models in ventilation flow research and practice, for forced mixing ventilation in a cubical enclosure driven by a transitional wall jet (i.e. Re ≈ 1,000 and Re ≈ 2,500).
Contributed by: T. van Hooff(*), B. Blocken(*), G.J.F. van Heijst(**) — (*)Dept. of Civil Engineering, KU Leuven, Belgium and Dept. of the Built Environment, Eindhoven University of Technology, the Netherlands.
(**)Dept. of Applied Physics, Eindhoven University of Technology, the Netherlands
© copyright ERCOFTAC 2024



