Flow behind a blunt trailing edge

Underlying Flow Regime 2-01 © copyright ERCOFTAC 2004

Test Case

Brief description of the study test case

The tests were performed in the VKI high-speed cold flow cascade tunnel. The three-blade cascade, used for the measurements is sketched in Figure 1 and the blade characteristics are given in Table 1.

The flow behind the blunt trailing edge was investigated by steady and unsteady measurements. The following steady measurements were performed: the surface pressure distribution on the central blade, the blade velocity (or the mid-span isentropic Mach number) distribution and the boundary layer velocity profiles. The unsteady character of investigated regime was monitored through the trailing edge pressure and the Schlieren images of the density field.

Two types of blades were instrumented. The first blade, denoted A, and shown in Figure 2, had a specially designed trailing edge consisting of a rotating cylinder with diameter of 20 mm. On the suction and pressure sides were mounted 31 and 22 wall pressure taps respectively, for blade velocity distributions. In the rotating cylinder, one Kulite pressure sensor was placed near an ordinary pneumatic pressure tapping.

Table 1: Blade characteristics
Chord length	C	280 mm
Pitch	P	196 mm
Blade height	H	200 mm
Stagger angle	Γ	-49^o83
Trailing edge thickness	D	15 mm
Trailing edge wedge angle	Є	7.5 deg
Gaging angle, (arcsin o/g)	*α^₂**	19.1 deg

The second blade, denoted B, shown in Figure 2, was equipped with 6 Kulite pressure sensors, each of them coupled with a pressure tap, identical to the Blade A case. This blade was instrumented in order to check the influence of the reward-facing step between the blade lip and the rotating cylinder and to provide data regarding the effects of vortex shedding on the upstream flow with respect to the trailing edge.

Figure 2: Blades instrumented in VKI cascade tunnel (fig.2 in Cicatelli and Sieverding (1997))

The flow conditions are specified in Table 2:

Table 2: Flow conditions
Inlet total temperature		293 K
Inlet total pressure		1178 mbar
Outlet Mach number		0.4
Reynolds number		2.8 x 10⁶
Turbulence level		1.15%

The two-dimensionality of flow was maintained by bordering the cascade with boundary layer fences. The efficiency of fences was confirmed by the oil flow visualization.

Test Case Experiments

As already mentioned, the experimental programme involved both stationary and unsteady measurements. The flow region was investigated by two types of measurement technique and using two types of blades instrumented with a fast responds pressure transducer and a pneumatic wall pressure tapping, which allowed to measure the steady and unsteady trailing edge pressure distribution.

In the stationary measurements the static pressure tapes distributed along the surface of the central blade have given the surface or base pressure distribution. Remarks on the pressure measurements accuracy are given in the part dedicated to the unsteady regime. This distribution, marked by empty diamonds, can be seen in Figure 3. The associated mid-span isentropic Mach number distribution is shown in Figure 4.

Figure 3: Surface (or base) pressure distribution (experiment: Fig. 9 Cicatelli and Sieverding (1997) and computation: fig.8 in Manna et al. (1997))

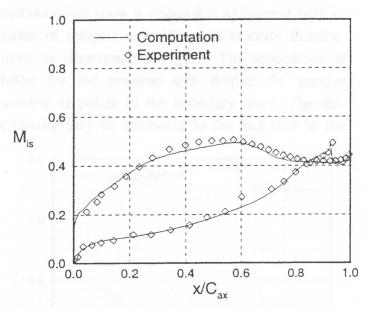
Figure 4: Isentropic Mach number distribution (experiment: Fig. 6 Cicatelli and Sieverding (1997) and computation: fig.7 in Manna et al. (1997))

The boundary layer velocity profiles were captured with a flattened Pitot probe, with thickness of 0.25mm. The probe was placed in the upstream region, with respect to the trailing edge, at the distance of one diameter of the trailing edge diameter. The uncertainty in the probe position of ±0.05 mm was reported.

The velocity profiles are emphasized in Figure 5, shown by the empty markers. The evaluation of the characteristics of the boundary layers (see) as the shape factor, its displacement and momentum thickness showed that the pressure and suction side boundary layers are fully turbulent and the first one has a thickness equal with almost half of those of the second one.

Figure 5: Boundary layer velocity profiles (experiment: Fig. 7 Cicatelli and Sieverding (1997) and computation: fig.9 in Manna et al. (1997))

All quantities plotted at Fig. 3, 4 and 5 are tabulated at Table 1, 2 and 3 respectively (see appendix).

In the characteristics evaluation of the boundary layer profiles, a correction for the wall interference was taken into consideration.

In the unsteady measurements, the pressure were acquired with a BE490 acquisition card installed on a 486 DX4 100MHz PCI bus personal computer. The system has a maximum sampling frequency of 1 MHz with 12bits resolution. 8 channels were monitored at a sampling rate of 25kHz and 4096 samples were collected. Two channels were dedicated to the Kulite pressure transducer and one for the pneumatic static pressure tapping mounted in the parallel with the Kulite transducer. The signals from a Kulite pressure sensor and its pair pressure tap, the inlet total pressure and outlet static pressure

The error analysis indicated that the pressure tap measurements have an uncertainty of ±2% from the reference pressure and the Kulite pressure transducer gave an uncertainty of ±0.17%. Also the difference between the time averaged signals provided by the Kulite transducer and pneumatic pressure tap were below 2%.

The post-processing of the pressure signals were important to identifying the vortex shedding frequency and to check if any influence on the upstream flow with respect to the trailing edge exists. For such reason, the pressure signal was decomposed in a time averaged component ${\bar {P}}$ and fluctuating one ${\tilde {P}}$ :

P={\bar {P}}+{\tilde {P}}\qquad \qquad \qquad (1)

The time-averaged component was extracted from the signal offered by the pneumatic pressure tap and the fluctuating component given by the Kulite transducer.

Figure 6: Schlieren pictures for vortex shedding phenomenon (Fig. 13 Cicatelli and Sieverding (1997))

The vortex shedding frequency f was obtained by applying an FFT analysis to the fluctuating component. The Strouhal number S was computed as follows:

S=fD/u\qquad \qquad \qquad \qquad (2)

where u is the downstream velocity. A value of 0.27 was obtained for the Strouhal number that correspond to a vortex sheding frequency of 2.65 kHz.

It was assumed that the fluctuating component can also be decomposed as:

{\tilde {P}}=P^{\prime }+P_{\text{pha}}\qquad \qquad \qquad (3)

The first component in (3) is associated to the small scale turbulent structures and the second one to the vortical structures, placed in the von Karman vortex street. This second component is obtained by phase averaging the component

This was done by chopping the signal in samples with the length equal to the time-period given by the vortex shedding frequency . The obtained samples were ensemble or phase averaged. This component that showed an almost sinusoidal variation, allowed observing that the vortex shedding phenomenon was felt far in the upstream flow.

The vortex-shedding phenomenon was further investigated with a Schlieren technique that uses a Nanolite high-speed system, which was constructed by Impulsphysik. The high-resolution pictures captured the vortex formation (see Figure 6) and allowed the extraction of the boundary layer size. The suction side boundary layer thickness, measured in the pictures is of 4-5 mm, and it is in good agreement with data given in namely Table 3, 4.1 mm.

CFD Methods

The study test cases were calculated with RANS methods. The 2D unsteady equations were solved, but two types of calculations were carried out: One to simulate the time-averaged steady state yielding the steady pressure distribution on the trailing edge and one to simulate the unsteady behaviour yielding the vortex shedding frequency and by averaging also the velocity distribution on the pressure and suction side. The numerical differences between the two calculations are provided below.

In what follows, we present the numerical technique used by Manna et al. (1997), with the state of the art algorithm usually employed in the CFD turbomachinery research using own code. We mention that Magagnato (1999) has used a similar technique. The difference between the two approaches is in the spatial discretization and the applied turbulence model.

The governing system is written in the fully conservative form and it is discretized using a cell center formulation on a structured mesh. The convective cell face flux is discretized with the approximate Riemann solver of Roe. The TVD high order scheme is obtained based on the Van Leer's MUSCL approach with a min-mod limiter.

Explicit time discretization is achieved by a five-stage Runge-Kutta scheme. For the steady state computations, the convergence is accelerated by a FAS multigrid technique with the aim of providing reasonable initial conditions for the unsteady calculation. The unsteady 2D N-S questions have been integrated over large time. At this process we do not care about accuracy in time. The aim was to rich the steady-state solution. The turbulence is accounted through the Baldwin-Lomax algebraic mixing length model.

Regarding the grid, Manna et al. (1997) emphasized the role of the grid refinement and control of the numerical viscosity, when simulating wake-like effects. The O-type mesh has been arranged around the blade and H-type mesh blocks has been placed in the far wake regions (see Figure 7). The total number of grid points was 43770 and the mesh spacing in the transversal direction to the wall was around . This value sufficient for numerical calculations and it was indicated in paper (references). A grid sensitivity study has only been carried out for steady state calculations, computations not shows herein indicate that a grid system of about 34000 points delivers very similar predictions in terms of aerodynamic performances.
For walls, a zero normal pressure gradient was accepted and was considered adiabatic.

Physical inlet boundary conditions are specified through the stagnation temperature, the stagnation pressure and flow angle, while for the numerical boundary condition the normal momentum equation is applied. At the outlet the static pressure is fixed, while all other variables are obtained by first order extrapolation. For walls, a zero normal pressure gradient was accepted and was considered adiabatic. Solid wall boundary conditions are strongly enforced with a mirror cell approach for the velocity filed. Further, the wall is assumed to be adiabatic, and the normal pressure gradient is imposed to be zero. Connectivity boundary conditions are provided by means of a two layer set of dummy variables which are filled the appropriate values from the neighboring block in order to ensure that the numerical flux calculation remains unchanged when crossing the internal boundary. All physical boundary conditions are specified in accordance with the experimental setting.