Airflow in the human upper airways

Application Challenge AC7-02 © copyright ERCOFTAC 2020

Description

Introduction

In the current application challenge (AC), in vitro velocity measurements using particle image velocimetry (PIV), Large Eddy Simulations (LES) and Reynolds-Averaged Navier-Stokes (RANS) have been conducted in a human-based model of the upper airways (shown in figure 3). This AC is a direct follow up of the application challenge “AC7-01:Aerosol deposition in the human upper airways” and provides the corresponding flow velocity data. The investigations were performed for steady-state inhalation at a flow rate of 60 L/min. The flow conditions at these flowrates are in the turbulent regime. LES and RANS simulations were carried out in the same geometry and under the same ventilation conditions. The methods and results described in the present application challenge are mainly adopted from Janke et al. (2019) (experimental part) and Koullapis et al. (2018) (numerical part).

Relevance to Industrial Sector

Aerosolized delivery of drugs to the lungs is used to treat a number of respiratory diseases. Regional deposition effects play a critical role in applications where targeted drug delivery is needed in order to maximize efficacy and minimize side-effects. Quantifying regional deposition is therefore important in assessing and optimizing treatment. Validated computational fluid-particle dynamics methods offer a powerful tool to predict airflow and localized deposition in the respiratory airways, in order to further our understanding of the flow and aerosol dynamics, and test and optimize inhaler therapies. However, accurate and efficient numerical simulations of the respiratory airways pose a challenge due to the complexities associated with the airway geometry, the flow dynamics and the aerosol physics. Numerical studies conducted to date have adopted a variety of computational techniques, a range of airway geometries varying in complexity, and differing assumptions on the flow and aerosol physics. In addition to the wide variability in the modelling approaches, validation of CFD methods in the respiratory airways is limited. The objective of the current application challenge is to present a benchmark case that can be used for the validation of computational tools intended for regional deposition studies in the upper airways. In this part, in vitro velocity measurements in a complex realistic geometry are provided at various inhalation flow rates. CFD (LES and RANS) results are then compared against the measured data and best practice guidelines for accurate numerical predictions of airflow inside the human upper airways are suggested.

Design or Assessment Parameters

Mean in-plane velocity magnitudes and turbulent kinetic energy fields were measured and numerically predicted at three planes within a realistic model of the human upper airways. The procedure to calculate these fields in the PIV experiments is described in section Boundary conditions.

Flow Domain Geometry

The description that follows was adopted from Lizal et al. (2012). The model basically comes from two distinct realistic geometries that were carefully connected in the trachea. These are described separately in the following sections. The geometry segments can be found and downloaded in stl format in AC7-01. The numbering of the stl segments is the one shown in ﬁgure 4. However, the 10 larger outlet segments along with their attached outlet patches are separated from the airway branches (segments 13-22) and are designated as segments 23-32 (segment 13 is attached to outlet segment 23, segment 14 is attached to outlet segment 24 and so on).

Digital reference model of bronchial tree

The digital reference model of Schmidt et al. (2004) served as a basis for the new model. The original geometry was produced by high resolution computerized tomography (HRCT) of an excised lung of an adult male free of pathological alterations. Their model development uses special image processing algorithms for the segmentation and delineation of the bronchi. The model does not include upper airways, it begins with trachea and spans down to the 17th generation of branching. Our model currently extends only to the seventh bifurcation, but geometry through the 17th Horsfield order is available and could be used for a more complete airway model. The measured branching angles are shown in figure 1 (Lizal et al., 2012). The Schmidt’s geometry was supplemented with the oral cavity described in the following paragraph.

Figure 1: Branching angles of tracheobronchial airways.

The oral cavity

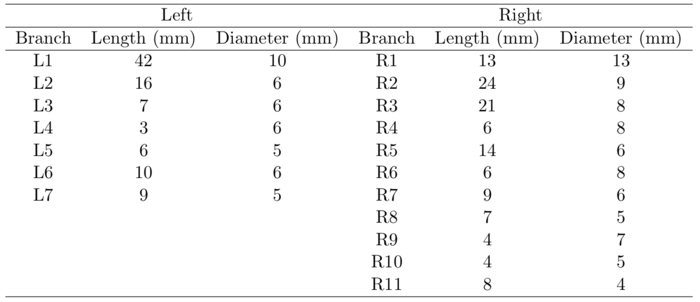
The upper part of the Lovelace Respiratory Research Institute’s (LRRI) ‘’A model‘’ (Zhou & Cheng, 2005) was used to construct the current model. The anterior oral cavity was molded from in vivo dental impression of a living Caucasian male at approximately 50 percent of the full opening (Lizal et al., 2015). The wax model provided by LRRI was scanned by an Atos (GOM) device, converted to STL format, and concatenated with our original model at the trachea (Figure 3). The dimensions of current models are summarized in Tables 1 and 2. In Table 2, the dimensions of the current model are compared to previously published model geometries.

Table 1: Dimensions of the realistic model (notation corresponds to Figure 2).

Table 2: Comparison of published model geometries.

Figure 2: A scheme of the model with nomenclature used for the description of dimensions.

Figure 3: Flow domain in the current model of the upper airways.

Manufacturing of the physical model for flow measurements

In order to perform PIV measurements, the seeded flow needs to be optically accessible. Therefore, a transparent, cast silicone model (Elastosil, RT 601, n = 1.4095) was manufactured. At first, the inner geometry (see figure 3) was divided in thirteen parts and each single segment was 3D printed via fused deposition modeling (FDM) using acrylonitrile butadiene styrene (ABS). In a next step, all single parts were joint together to form two final larger segments. The first (upper) one incorporates the mouth cavity, the larynx, the pharynx as well as the upper trachea. The lower part of the model features the lower trachea, the main bifurcation and bronchi and the following branching generations. To reduce surface roughness, the cores were sanded and coated with a thin layer of water solvable glue. After casting and curing of the silicone resin, the cores were removed by submerging the model in acetone and by rinsing with water, consecutively. Both parts of the whole model were mounted at an aluminum lid with additional connecting adapters (see figure 4).

Figure 4: Photograph of the measurement setup within the upper part of the model (a); CAD rendering of the mounting construction for the transparent silicone model (b).

Limitations of the model

The users of the model should be aware of its limitations. Some of the following points arose from discussion with experts from the medical community. The first question concerns the realism of combining two realistic geometries. It should be noted, that acquiring the complete realistic geometry is complicated, as there are different requirements for imaging the oral cavity and the tracheobronchial airways. And even when one subject was imaged during two different sessions, the airway dimensions would change and thus the created geometry would not truly represent the real airways at a certain instant. Combining two well-defined geometries in our case forms a realistic, although, non-specific individual geometry. It should also be emphasized that the current model serves primarily for comparison of experiments and numerical simulations, and therefore the combined geometry is acceptable. Another remark concerns the circular connection of the two geometries. As both the geometries had realistic cross-sections in the connecting region in trachea, it was necessary to provide the transition from one to another. In our case we selected the circular shape as the optimal transition, since the lower geometry began with a circular-like shape. Another frequent question concerns the moving boundaries. The model is rigid and therefore the boundaries do not move. In reality, trachea and the main bronchi are supported by cartilages and do not contract or stretch significantly. However, the more distal airways are not perfectly rigid and there could be significant motion as we move in the terminal bronchioles. Instead of air, a water-glycerin mixture is used as the working fluid during the experiments. This is legitimate as long as the relation of inertia to friction as expressed by the Reynolds number is maintained. Nevertheless, certain effects cannot be accounted for this way, such as the heating of the air within the human body or the effect of air humidity.

Flow Physics and Fluid Dynamics Data

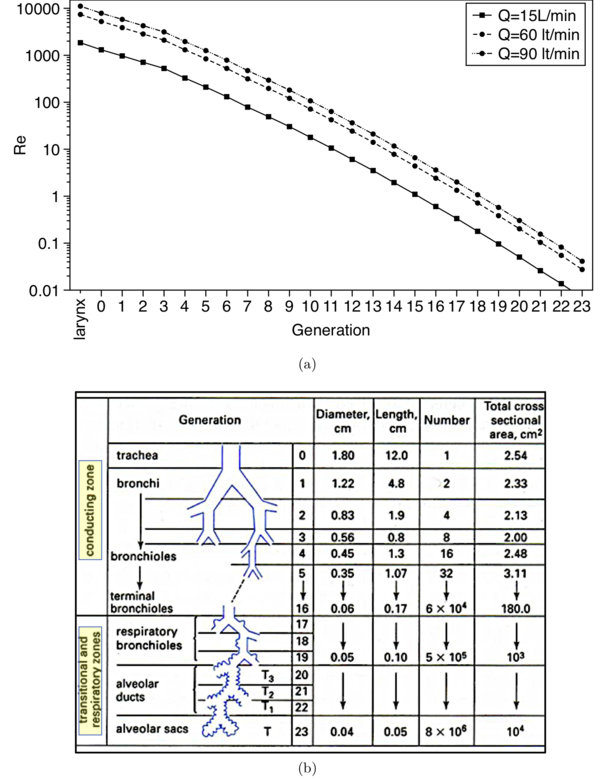
Airflow in the upper airways is incompressible and is assumed herein isothermal, although in reality there is heat exchange between the airway walls and the incoming ambient air. Depending on the inhalation flowrate, airflow in the human upper airways can enter the upper airways -the mouth or the nose- in the laminar or turbulent regime. Figure 5(a) plots the local Reynolds number versus airway generation number for three inhalation flowrates, 15, 60 and 90 L/min, which are typical for quiet breathing and inhalation through high and low resistance inhalers, respectively. The correspondence between generations and airway branches is shown in the schematic of figure 5(b). Even when the flow starts laminar, it usually transitions to turbulence due to geometric effects, such as the bent in the oropharyngeal region and the constriction at the laryngeal glottis, just upstream the trachea (see figure 25). The characteristics of the laryngeal jet, which forms at the glottis constriction and produces high turbulence levels (Lin et al., 2007), bear a resemblance to the flow through a constricted pipe. This type of flow can be classified as a free shear flow where the wall serves to confine the spreading of the jet rather than producing turbulence (Tawhai & Lin, 2011). As we move deeper in the airways (higher generation number), the local Reynolds number decreases due to the overall increase of cross sectional area that the air passes through (see figure 5(b)), which results in lower air velocities in the airway branches (figure 5). However, turbulent eddies generated in the upper airways may propagate into airway generations that would normally carry laminar flow based on their local Reynolds number. Zhang & Kleinstreuer (2004) predicted numerically that turbulent fluctuations from the trachea can persist downstream to third generation at inspiratory flowrates higher than 30 L/min. Similar observations were made by Lin et al. (2007) using a patient-specific airway model and a more advanced flow solver. Turbulent effects eventually dissipate in the central airways, approximately in generations 4-6, and the flow becomes laminar. In the present AC, numerical simulations at an inhalation flowrate of 60 L/min are carried out. The Reynolds number in the trachea of the present model is:

$Re_{T}={\frac {u_{T}D_{trachea}}{v}}\qquad (1)$

where $u_{T}$ is the bulk velocity in the trachea, $D_{trachea}$ = 16.3mm is the diameter of trachea and v the kinematic viscosity. Due to limitations in the operation of the experimental facility, which are discussed in section Measurement errors, a maximum Reynolds number of 4286 in the trachea could be reached. The corresponding water flowrate through the model in the PIV experiments was $Q_{w/g}$ = 28.56 L/min ( $u_{T}$ = 2.21 m/s). Despite the above mentioned limitation of the experimental setup, the developed flow is well within the turbulent regime.

Figure 5: (a) Local Reynolds number versus airway generation number for three inhalation flowrates, 15, 60 and 90 L/min. (b) Schematic of the airway generations in the human adult lung. Diameters, lengths, number of branches and total cross sectional area in a particular generation are reported. (redrawn from Weibel (1963)).

Contributed by: P. Koullapis^a, J. Muela^b, O. Lehmkuhl^c, F. Lizal^d, J. Jedelsky^d, M. Jicha^d, T. Janke^e, K. Bauer^e, M. Sommerfeld^f, S. C. Kassinos^a —
^aDepartment of Mechanical and Manufacturing Engineering, University of Cyprus, Nicosia, Cyprus
^bHeat and Mass Transfer Technological Centre, Universitat Politècnica de Catalunya, Terrassa, Spain
^cBarcelona Supercomputing center, Barcelona, Spain
^dFaculty of Mechanical Engineering, Brno University of Technology, Brno, Czech Republic
^eInstitute of Mechanics and Fluid Dynamics, TU Bergakademie Freiberg, Freiberg, Germany
^fInstitute Process Engineering, Otto von Guericke University, Halle (Saale), Germany