UFR 1-06 Description

Front Page

Description

Test Case Studies

Evaluation

Best Practice Advice

References

Description

Preface

This document focusses on the underlying flow of the fully-developed, steady, vertical, axisymmetric (round) plume flowing in a still and unstratified environment. This includes consideration of both rising, positively-buoyant plumes and falling, dense, negatively-buoyant plumes. Only turbulent plumes are considered as this covers nearly all relevant engineering and environmental applications. For a review of laminar plumes, see .

This UFR is relevant to the Application Challenges AC3-05 on buoyant gas air-mixing, AC4-03 on air flows in an open plan air-conditioned office, and AC4-04 on tunnel fires, and to UFR4-09 on confined buoyant plumes.

Overview of the UFR

Free vertical buoyant plumes and free-jets are related phenomena, both having a core region of higher momentum flow surrounded by shear layers bounding regions of quiescent fluid. However, whereas for jets the driving force for the fluid motion is a pressure drop through an orifice, for plumes the driving force is buoyancy due to gradients in fluid density. Plumes can develop due to density gradients caused by temperature differences, for example in fires, or can be generated by fluids of different density mixing (e.g. hydrogen releases in air). There are many flows of both engineering and environmental importance that feature buoyant plumes, ranging from flows in cooling towers and heat exchangers to large geothermal events such as volcanic eruptions. For a good introduction to turbulent jets and plumes, see Chen & Rodi [1] or List [6][7]. A more general discussion of buoyant flows is given in Gebhart et al. [4].

Figure 1 Flow development of a buoyant jet, from Chen & Rodi [1]

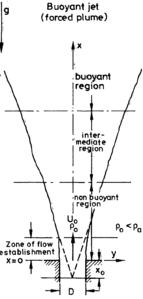
A free vertical buoyant plume can be split into a number of regions, see Figure 1. Close to the source, the flow is affected by details of the particular release conditions. This could include inertial effects if, for example, the flow involves a release of buoyant fluid through a nozzle under pressure, or, perhaps, other complexities associated with combustion in fire plumes. At a sufficient distance further downstream, the effects of the source conditions are lost, buoyancy forces dominate the flow and it exhibits plume behaviour. Between the near-source and far-field regions, there is a transitional region.

Plumes arising from continuous releases of buoyant fluid with significant initial momentum are classified as forced plumes or buoyant jets. Those involving a discrete release of buoyant fluid are termed thermals or puffs (e.g. as caused by an explosion), and starting plumes refer to the advancing front from a continuous buoyancy source in the initial phase of the release before a steady plume becomes established.

Buoyant jets (i.e. plumes with significant initial momentum) occur in a number of important practical applications such as the flow from smokestacks and cooling-water discharges into reservoirs. It is important in these cases to be able to identify when the transition occurs from jet-like behaviour near the source to plume-like behaviour in the far field. A common dimensionless parameter used to distinguish these two flow regions is the densimetric Froude number, Fr, given by:

${Fr}={\frac {U}{\sqrt {\left[gD\left({\frac {\rho _{\infty }-\rho }{\rho _{\infty }}}\right)\right]}}}$

where U is the mean velocity, g gravity, D a characteristic length-scale, and ρ density. Subscript ∞ refers to the far-field value. The Froude number represents the ratio of inertial forces to buoyancy forces. It ranges in value from near zero for pure plumes, towards infinity for jets with negligible buoyancy. Chen & Rodi analysed a number of jet and plume experiments and, using dimensional analysis, produced the graph reproduced in Figure 2, which shows the transition from jet- to plume-like behaviour with increasing Fr.

Figure 2 shows how the difference in mean density between the axis of the plume and the far field value decays with distance from the inlet. In the jet-like region near the source, the density difference decays at a rate (x – x₀)^-1 whereas in the fully-developed plume region it decays faster at (x – x₀)^-5/3. Here, x is the axial coordinate and x₀ is the “virtual” source location, see Figure 1. Empirical correlations for the decay rate of mean velocity and scalars in buoyant jets are given in Gebhart et al. [4]. Both jets and plumes spread linearly in a uniform environment, although at different rates. Empirical correlations for the spreading rate in plumes are given later.

Another common measure used to assess when buoyant jets reach a fully-developed state is the Morton length scale, $l_{M}$:

$l_{M}={\frac {M_{0}^{3/4}}{F_{0}^{1/2}}}$

where M₀ and F₀ are the specific momentum and buoyancy added at the source of the plume:

$M_{0}=2\pi \int _{0}^{r_{0}}U^{2}r\ dr\qquad \qquad F_{0}=2\pi \int _{0}^{r_{0}}U_{g}{\frac {\Delta \rho }{\rho _{\infty }}}r\ dr$

For plumes with uniform properties at the source, this is equivalent to:

$l_{m}={\frac {Fr_{0}D}{(\pi /4)^{1/4}}}$

where Fr₀ is the the source densimetric Froude number at the source and D the inlet source diameter.

Figure 2 Decay of centreline density in round plumes from Chen & Rodi [1]

Papanicolau & List [9] suggest that jet-like conditions occur in turbulent buoyant jets for $(x-x_{0})/l_{m}<1$and fully-developed plume-like conditions for $(x-x_{0})/l_{m}>5$. However, there is some debate in the literature over the distance required to reach fully-developed plume conditions, see for example Dai et al [10] and Shabbir & George [11]. Mean parameters (velocity, temperature etc.) require a shorter distance to reach a fully-developed state than statistical quantities such as Reynolds stresses.

An important feature of the mean flow in the fully-developed region of turbulent buoyant plumes is “self-similarity” or “self-preserving” behaviour. In positively-buoyant plumes, as the less dense fluid rises and spreads, the mean velocity peak on the plume centreline decays and the plume becomes wider. However, the shape of the mean velocity profile remains the same. If the dimensionless radial profiles of the mean velocity are plotted at different vertical positions in the plume on the same graph axes, the curves all fall on top of one another. Self-similarity is also exhibited in the dimensionless temperature and species concentration profiles and in the dimensionless RMS turbulent fluctuations of velocity, temperature and concentration $\left({\sqrt {u^{2}}}/U_{0}\right.$, ${\sqrt {\nu ^{2}}}/U_{0}$, ${\sqrt {\theta ^{2}}}/\Theta _{0}$ or $\left.{\sqrt {c^{2}}}/C_{0}\right)$. Sample data from the experiments of Papanicolaou & List [9] and Dai et al [10] shown in Figures 3 and 4 demonstrate this behaviour.

Figure 3 Dimensionless mean velocity and mean concentrations profiles in a turbulent axisymmetric plume, from Papaanicolaou & List [9]

Figure 4 Dimensionless mixture fraction fluctuation profiles in a turbulent axisymmetric plume, from Dai et al [10]

Plume Analysis Based on Integral Equations

One means of analysing the flow behaviour of self-similar buoyant plumes is to use integral methods. This involves assuming profiles for the velocity, temperature and concentration based on experimental observations. The mean flow equations are then integrated over the whole plume cross-section to produce ordinary differential equations. The entrainment rate is also assumed, usually as a function of the local centreline velocity.

Theoretical analysis of self-similar plumes using integral methods began more than 50 years ago with the works of Yih [12], Rouse et al [13], Batchelor [14] and Morton et al [15] for plumes with small density differences in unstratified and stratified environments. More recently, these theories have been extended to consider plumes with significant density differences [16][16], with unsteady source strengths  [18][19][20] and fire plumes [21][22] [23][24].

The simplest analysis proceeds by assuming that the velocity and buoyancy force are constant across the plume and zero outside it (i.e. a 'top hat' profile). Transport equations for the conservation of volume, momentum and density deficit are integrated analytically with respect to the vertical distance, x, to arrive at expressions for the plume radius, b, the vertical velocity, U, and the density, ρ, inside the plume:

File:Nextbit html 412bfc30.gif File:Nextbit html m4f4676a7.gif File:Nextbit html m4bfad357.gif (5)

where ρ₁ is a reference density, α is an empirical entrainment coefficient and Q is the buoyancy flux, given by:

File:Nextbit html m30a835d5.gif (6)

The empirical entrainment coefficient, α, relates the entrainment velocity, U_e, to the plume velocity (U_e = αU). This analysis was first published by Schmidt [schmidt41] and is described in Morton et al. [morton56].

Morton et al. [morton56] extended the above approach, assuming Gaussian radial profiles for the velocity and buoyancy force instead of top-hat profiles. They found that the spreading rate of the plume (db/dx) was equal to 6α/5 and was independent of the strength of the buoyancy source. In their analysis they defined the plume radius, b, as the point where the velocity fell to e^-1 of its centreline value (0.37U_c). Experiments undertaken by Morton et al. [morton56] of positively buoyant plumes in stratified saline solutions found the entrainment coefficient to be around α = 0.093. More recent studies have suggested a value of α ≈ 0.082 for plumes in unstratified environments (for comparison, the entrainment constant for pure jets is α ≈ 0.057) [geb88][linden00].

Recently, Diez & Dahm [dd07] developed an alternative integral approach that does not rely upon the entrainment coefficient, α. Instead, it uses the integral equation for the momentum flux to develop an equation for the local centreline velocity. Diez & Dahm's model relies upon a parameter, c_δ, which experiments show to be constant in the far-field of both jets and plumes.

Further details of integral methods applied to plumes and jets, including discussion of empirical models for α as a function of the Froude number, can be found in Chen & Rodi [cr80] and Gebhart et al. [geb88].

Whilst integral methods can provide accurate results for relatively simple plumes it is difficult to extend the approach to model more complex turbulent flows, where for example the plume may hit a wall or encounter regions of flow recirculation. To study these more complex flows, a more general-purpose CFD approach must be used.

Review of UFR studies and choice of test case

Front Page

Description

Test Case Studies

Evaluation

Best Practice Advice

References

Contributed by: Simon Gant — Lea Associates

© copyright ERCOFTAC 2010