UFR 1-06 Evaluation
Axisymmetric buoyant far-field plume
Underlying Flow Regime 1-06
Comparison of CFD Calculations with Experiments
Van Maele & Merci [2] presented the results from a number of simulations that examined the effects of different combinations of models and approximations. The Boussinesq approximation was shown to have no affect on the model predictions when the SGDH model was used. Indeed, the SGDH source term itself had a negligible influence on the results. When using the GGDH source term, however, the Boussinesq approximation had an effect on the results nearest to the plume exit at z/D = 12, where the assumption of caused an increase in the peak velocity of around 5%. By assuming that the mean density was the same as the reference density, the buoyancy source term became smaller and so the turbulent kinetic energy and hence the eddy viscosity were also smaller. As a consequence, there was less mixing, the centreline velocity increased and the spreading rate decreased. The effect was significant where the mean density differed most from the reference density, nearest to the plume source, but was negligible in the far field. These results suggest that the Boussinesq approximation can be used in the far field of buoyant plumes where density differences are small. However, if the CFD domain extends from the far field to the source of buoyancy, such as a fire or strongly heated surface where density differences are appreciable, then the Boussinesq approximation should not be used.
It should also be remembered that Van Maele & Merci’s
interpretation of the ‘Boussineq
approximation’ only involved setting
in the production term, G.
The density and other flow properties (molecular viscosity,
specific heat etc.) still varied as a function of temperature elsewhere
in the transport equations.
Van Maele & Merci examined the effects of SGDH versus GGDH and the
effect of switching on and off both the production due to buoyancy
term, G, and the source term in the ε–equation, SεB,
on the standard and realizable k – ε
models. Table 4 summarizes the cases tested. In the relevant cases,
they used the full buoyancy source term G rather than any
truncated form of the equation. The ε–equations
were different for standard and realizable models, but in both cases,
where used, the buoyancy-related source term was given by:
The results were compared to the experimental data of George&'et al. [3]
and the correlations of Shabbir & George [11]
which were given by:
| Axial velocity: |
| Buoyancy: |
where W is the mean axial momentum, ΔT is the
difference between the local mean and ambient temperatures, z
is the vertical distance from the source, η = r/z
is the similarity variable (r is the
radial distance from the plume centreline), and β the
thermal expansion coefficient. The buoyancy added at the source,
F0 , is found from :
and was 1.0 × 10-6 cm4/s3
in the George et al. plume [3].
To compare to these empirical correlations,
Van Maele & Merci used their results taken at a position, z = 1.75 m,
equivalent to approximately 28 inlet diameters from the source.
To demonstrate that this was sufficiently far from the source to
produce self-similar profiles, the dimensionless velocity and
temperature profiles were shown to be practically identical at a
distance of 2.75 m.
Profiles of the mean axial velocity and buoyancy are compared to the
empirical correlations in Figures 7 and 8. A summary of the centreline
values and spreading rates for velocity and temperature are given in
Table 5. This shows the measured values from the experiments of
George et al. [3],
the recommended values given by
Chen & Rodi [1]
from their analysis of plume experiments up to
1980, the subsequent measured values from
Shabbir & George [11],
the RANS results from Van Maele & Merci [2] and
Hossain & Rodi, and the LES results from
Zhou et al. [28]. Three results are taken from
Hossain & Rodi: Case A which is from a k – ε model without
any buoyancy modifications, Case B which is from a k – ε
model with buoyancy corrections in both k and ε
equations, and Case C which is from
Hossain & Rodi’s algebraic stress/flux model.
For the Van Maele & Merci [2] results,
both the standard and
realizable k – ε models without buoyancy
modifications (cases SKE and RKE) predicted overly large centreline
velocity and buoyancy values and under-predicted the spreading rates of
the plume. When the SGDH source term was used, with or without
SεB , it had practically
no effect on the results. This may have been partly due to the
particular choice of the constant
cε3
which made the contribution from the buoyancy production small
relatively to shear production in the ε-equation.
The SKE, SKE_A and SKE_A* cases all returned very
similar predictions to each other and RKE, RKE_A and RKE_A* cases
behaved similarly. This was shown by Van Maele & Merci to be a
consequence of the SGDH source term being negligible in comparison to
other terms in the k and ε equations.
Table 5 shows that for the basic k – ε model
without any buoyancy corrections there are significant differences in
terms of the predicted spreading rates between the results of
Van Maele & Merci [2] and
Hossain & Rodi [8] (cases SKE
and A, respectively).
Van Maele & Merci’s predictions
of the spreading rates are nearly 20% higher. This may have been due
to the choice of non-standard model constants by
Hossain & Rodi [8]
who used cμ = 0.109 and
σt = 0.614, whilst
Van Maele & Merci [2]
used cμ = 0.09 and σt = 0.85.
The results for the k – ε
model with buoyancy corrections are more similar (Cases
SKE_A and B, respectively). Here, in addition to the non-standard
cμ and σt
constants, Hossain & Rodi [8]
used a model with constant cε3
scaled by the Richardson number, which was zero in
the vertical buoyant plume, such that the buoyancy production had the
same weight as the shear production.
Use of the GGDH model produced some improvements in the results
presented by Van Maele & Merci [2].
For the SKE_B model, the
centreline value was well-predicted but the half-width of the plume was
overpredicted by around 20%. When the buoyancy source term in the
ε-equation was omitted (case SKE_B*) the axial
velocity on the centreline was reduced and the half-width prediction
became even more inaccurate. This is consistent in the SKE_B* case
with the turbulent kinetic energy being overpredicted due to the
removal of a positive source in the ε-equation.
For the realizable model with GGDH, the mean axial velocity and buoyancy
were over-predicted on the centreline by around 10% and 20%
respectively but the half-width was reasonably close to the
experimental values. Switching off the buoyancy-related source term in
the ε-equation (case RKE_B*) led to a slight
improvement in the results, however Van Maele & Merci noted that this
also reduced the numerical stability of the calculation. Details of any
source-term linearisation used to improve robustness are not provided
in their paper. They recommended that the SεB term should be
retained in the modelled equations to avoid convergence difficulties.
Van Maele & Merci commented that, overall, the GGDH variant of the
realizable model (RKE_B) performed better than the equivalent standard
k – ε model (SKE_B). However, the standard
model gave better peak mean axial velocity and buoyancy predictions
(to within 2% and 10%, respectively, compared to 10% and 25% for
the RKE_B model). It could also be argued that the realizable model
only gives good predictions for the plume half-width because the
predicted profiles happen to cross the experiment profiles at the
correct position, the actual shape of the predicted profiles are
incorrect. One could conclude, perhaps, that both standard and
realizable models predict the axisymmetric plume to a similar overall
level of accuracy. Neither provides an exact solution and the errors
for the two models are slightly different.
| Case Ref. | Turbulence Model | G | SεB |
| SKE | Standard k – ε | – | – |
| SKE_A | Standard k – ε | SGDH | Eqn (35) |
| SKE_A* | Standard k – ε | SGDH | – |
| SKE_B | Standard k – ε | GGDH | Eqn (35) |
| SKE_B* | Standard k – ε | GGDH | – |
| RKE | Realizable k – ε | – | – |
| RKE_A | Realizable k – ε | SGDH | Eqn (35) |
| RKE_A* | Realizable k – ε | SGDH | – |
| RKE_B | Realizable k – ε | GGDH | Eqn (35) |
| RKE_B* | Realizable k – ε | GGDH | – |
| (WF0-1/3z1/3)c | lW/2 | (gβΛTF0-2/3z5/3)c | lΔT/2 | |
| George et al. [3] experiments | 3.4 | 0.112 | 9.1 | 0.104 |
| Chen & Rodi [1] recommendation | 3.5 | 0.112 | 9.35 | 0.10 |
| Shabbir & George [11] experiments | 3.4 | 0.107 | 9.4 | 0.10 |
| SKE | 4.08 | 0.097 | 12.76 | 0.089 |
| SKE_A | 4.04 | 0.098 | 12.59 | 0.089 |
| SKE_A* | 4.04 | 0.098 | 12.55 | 0.089 |
| SKE_B | 3.32 | 0.132 | 8.48 | 0.119 |
| SKE_B* | 3.09 | 0.147 | 7.35 | 0.132 |
| RKE | 4.35 | 0.084 | 15.55 | 0.079 |
| RKE_A | 4.31 | 0.085 | 15.36 | 0.080 |
| RKE_A* | 4.3 | 0.085 | 15.31 | 0.080 |
| RKE_B | 3.74 | 0.103 | 11.78 | 0.098 |
| RKE_B* | 3.62 | 0.108 | 11.09 | 0.103 |
| Hossain & Rodi [8] CFD A | — | 0.079 | — | 0.076 |
| Hossain & Rodi [8] CFD B | — | 0.100 | — | 0.095 |
| Hossain & Rodi [8] CFD C | 3.50 | 0.109 | 8.22 | 0.100 |
| Zhou et al LES [28] | — | 0.111 | — | 0.105 |
Van Maele & Merci also presented results for the streamwise and radial
normal Reynolds stresses, and
(not shown here). None of the models tested
were capable of resolving the anisotropy in the normal stresses,
although this is not unexpected since eddy-viscosity models like those
tested by Van Maele & Merci were not designed to determine individual
normal Reynolds stresses, only their sum, the turbulent kinetic energy.
In the experiments, the streamwise stress was greater than the radial
stress on the centreline, . The linear k – ε
models on the other hand all gave . Shear stresses were also not predicted very
well and models overpredicted the peak value by up to 25%.
Plots of the k-profiles for standard and realizable models
are shown in Figure 9. When normalized using similarity variables all
of the models produced an off-axis peak in k which was not
present in the experiments. Similar behaviour was observed in plane
plumes by Yan & Holmstedt [53].
All standard k – ε
model variants underpredicted the centreline turbulent
kinetic energy by around 15% whereas the realizable models were all in
good agreement with the experiments. However, none of the model
variants captured the correct shape of the k-profile.
Comparison to Other Model Predictions
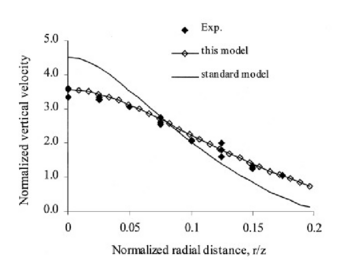
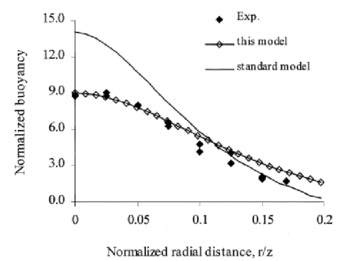
To provide some comparison to other models’ performance in this flow, the results of Yan & Holmstedt [53] are shown in Figure 10 for the George et al. [3] axisymmetric plume. The “standard model” they refer to is a standard k – ε model with SGDH, whilst “this model” is a modified k – ε model with GGDH that uses an algebraic relation for the Reynolds stresses where they appear in the production term, Pk. The standard model results are in good agreement with those obtained by Van Maele & Merci for the same case. The results obtained using their modified model appear to be better than those obtained by Van Maele & Merci for the standard k – ε model with GGDH.
The predictions of mean velocity and temperature from
Hossain & Rodi [8]
using an Algebraic Stress Model (ASM) are shown in
Figure 11. As noted in Section 2.3.1, their model was derived from the
differential stress model of
Gibson & Launder [46].
Figure 11 shows that their predictions are in good agreement with the
measurements of George et al. [3].
The predicted plume centreline values and half-widths using their model are shown in
Table 5 (marked “Hossain & Rodi [8] CFD
C”). These exhibit the best agreement with the
measurements of George et al. [3]
of all the model variants tested.
LES predictions from Zhou et al. [28] of the mean
velocity and temperature for the experiments of
George et al. [3]
are shown in Figure 12. Very good agreement is
obtained although this may be partly a consequence of using centreline
values to make the mean parameters dimensionless. Radial profiles of
normalized RMS axial velocity and temperature were reported to produce
a similar trend to that observed in the experiments, and turbulence
levels within the experimental range [29], although the
centreline dimensionless temperature fluctuation was approximately
0.45, in good agreement with the measurements of
Papanicolaou & List [9]
and Dai et al. [10], but slightly
higher than the value of 0.40 reported by
George et al. [28].
Plume spreading rates and centreline values were
found to be strongly sensitive to the imposed turbulent fluctuations at
the inlet plane in the LES model. Axial velocity fluctuations with an
amplitude of 20% of the mean axial velocity were imposed at the inlet,
with or without azimuthal forcing, to match the predicted location of
the transition from laminar to turbulent flow to that observed in the
experiments. In the experiments, however, the turbulence intensity at
the inlet was reported to be approximately 0.5% [11].
at four axial positions compared to the experiments of George et al. [3], from the LES of
Zhou et al. [28].
Figure 13 shows the dimensionless mean axial velocity profiles from
Brescianini & Delichatsios [42].
Both the experimental results
of George et al. [3] and
Dai et al. [39]
are shown. The basic model “ke1
Model A” is a standard k – ε
model with SGDH. Other model results shown include
“keS Model B”: a parabolic k – ε
model based on the work of
Hanjalić & Launder [76]
which retains both shear and normal-stress
production terms, together with GGDH for the production term due to
buoyancy; “keS Model C1”: the same
k – ε model but with the streamwise turbulent
scalar flux determined using the algebraic model of
Hossain & Rodi [8]
and “keS Model C2”: an extension of the C1 model that retains
streamwise gradients of velocity and density. The three
“keS” model variants all produce
similar results that are in good agreement with the experiments of
George et al. [3].
Interestingly, the standard
k – ε model with SGDH produces results in good
agreement with the experimental data of Dai et al. [39]
but in poor agreement with the data of George et al. [3]
Brescianini & Delichatsios [42]
commented that the results of their assessment depend strongly upon
which set of experiments are used for comparison.
Brescianini & Delichatsios [42]. The quantity U on the y-axis is dimensionless and equivalent to (WF0-1/3z1/3)
in Van Maele & Merci's notation.
Summary
Van Maele & Merci’s [2] results for two different linear k – ε models have been presented for the axisymmetric buoyant plume of George et al. [3] Various modifications to the buoyancy treatment and other simplifications were tested. From this work, the following conclusions can be drawn:
- The Boussinesq approximation can be used to model the flow behaviour in far-field of buoyant plumes, where density differences are small. Nearer the source of buoyancy, where density differences are more appreciable, the approximation should be used with care. In Van Maele & Merci’s [2] study it was shown to have no effect if SGDH is used, but had a noticeable effect with GGDH.
- The SGDH buoyancy-production term, G, is calculated using the streamwise temperature gradient which is small in this flow and the term therefore has little effect on the mean flow behaviour. As a consequence, when using SGDH the turbulent kinetic energy is underpredicted, the plumes have overly large centreline velocity and temperature values and do not spread sufficiently quickly.
- Using GGDH instead of SGDH improves the mean flow predictions.
- Neglecting the buoyancy source term, SεB, in the ε-equation has a relatively minor effect on the results with GGDH but can cause numerical stability problems. It is therefore not recommended to neglect this term.
- Van Maele & Merci assert that the realizable k – ε model of Shih et al. [66] when combined with GGDH performs better than the standard k – ε model with GGDH. However, the overall improvement shown in their results is relatively modest, if present at all.
- Better predictions of the mean flow behaviour in the far-field of buoyant plumes have been obtained using the more sophisticated k – ε model of Yan & Holmstedt [52] and the ASM of Hossain & Rodi [8].
Contributed by: Simon Gant — UK Health & Safety Laboratory
© copyright ERCOFTAC 2010


















