DNS 1-3: Difference between revisions
| Line 7: | Line 7: | ||
__NOTOC__ | __NOTOC__ | ||
= Abstract = | = Abstract = | ||
The 3D (Stanford) Diffuser is identified as a case with complex internal corner flow and 3D separation, is well documented and has a relatively simple geometry. The diffuser has an inlet section, an expansion section and an outlet section (see Figure 1). The flow at the inlet is assumed to be fully developed. At the outlet, standard Dirichlet condition for the pressure is prescribed, a Reynolds number of 10000 will be considered. | The 3D (Stanford) Diffuser is identified as a case with complex internal corner flow and 3D separation, is well documented (see, e.g., test case UFR4-16) | ||
and has a relatively simple geometry. The diffuser has an inlet section, an expansion section and an outlet section (see Figure 1). The flow at the inlet is assumed to be fully developed. At the outlet, standard Dirichlet condition for the pressure is prescribed, a Reynolds number of 10000 will be considered. | |||
<div id="figure1"></div> | <div id="figure1"></div> | ||
Revision as of 08:47, 15 November 2021
Flow in a 3D diffuser
Abstract
The 3D (Stanford) Diffuser is identified as a case with complex internal corner flow and 3D separation, is well documented (see, e.g., test case UFR4-16)
and has a relatively simple geometry. The diffuser has an inlet section, an expansion section and an outlet section (see Figure 1). The flow at the inlet is assumed to be fully developed. At the outlet, standard Dirichlet condition for the pressure is prescribed, a Reynolds number of 10000 will be considered.
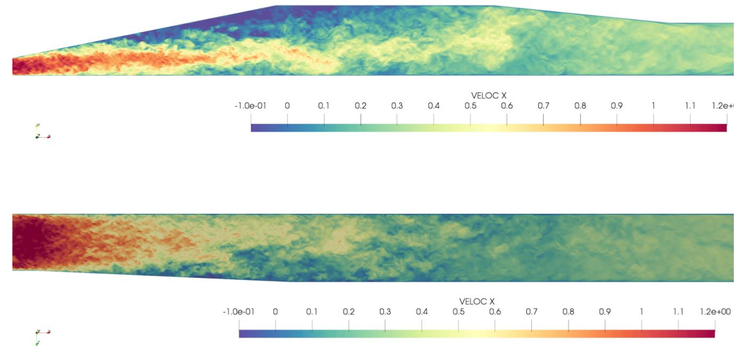
|
| Figure 1: Stanford double diffuser, Re=10000, preliminary validation. Non-dimensional instantaneous velocity at the two middle planes using Alya with 250 Million DoF and P2 polynomials. |
The results of this project will be used to assess computational strategies
(compressible vs incompressible DNS) and provide a rich database for verification and validation on subsequent computational campaigns.
Contributed by: Oriol Lehmkuhl, Arnau Miro — Barcelona Supercomputing Center (BSC)
© copyright ERCOFTAC 2024