Description AC2-09

Front Page

Description

Test Data

CFD Simulations

Evaluation

Best Practice Advice

SANDIA Flame D

Application Challenge AC2-09   © copyright ERCOFTAC 2024

Introduction

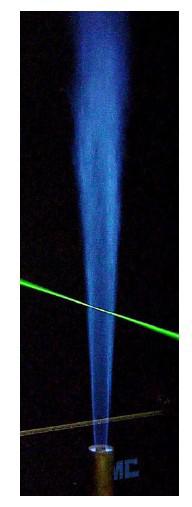
Sandia flame D [1] (shown in Fig.1) is a widely used test case for validation of numerical models of non-premixed combustion. The fuel stream is composed of 25% methane (CH4) and 75% air. The pilot flame is a lean mixture of C2H2, H2, air, CO2 and N2 with the same nominal enthalpy and equilibrium as methane/air at the equivalence ratio 0.77. Partial premixing with air also reduces the flame length and produces a more robust flame than pure CH4 or nitrogen-diluted CH4. Consequently, the flames may be operated at reasonably high Reynolds number with little or no local extinction, even with a modest pilot. The mixing rates are high enough that these flames burn as diffusion flames, with a single reaction zone near the stoichiometric mixture fraction and no indication of significant premixed reaction in the fuel-rich CH4/air mixtures. Flame D (Re=22400) has a small degree of local extinction. It can be assumed that the Flame D operates in a flamelet regime that means there is a scale separation between turbulence length and time scales and the scales characterizing the combustion process. Despite that the Sandia D Flame is not a demanding test case it seems to be worth to study various combustion/turbulence interaction models on this example as a starting point to more complex flame with local extinction and reignition. As an Application Challenge such a flame facilitates to study models of turbulence/chemistry interaction allowing to separate the influence of turbulence and turbulence/chemistry interaction models from the influence of chemical kinetics applied.

Focusing on the LES approach to the Sandia Flame D, one of the first 3D-LES of this flame type was presented by di Mare and Jones in 1999 [2] who applied simple steady flamelet model. Then a simplified Conditional Moment Closure (CMC) with the Conditional Source-term Estimation (CSE) proposed by Steiner and Bushe [3] was tested also on Sandia D. Very convincing results using unsteady-flamelet model were obtained by Pitsch and Steiner [4]. More recently the Conditional Moment Closure equations in the context of LES filtration were formulated by Navarro-Martinez et al. [5] and full CMC approach was validated using Sandia D flame. The LES-CMC approach was also applied by Garmory and Mastorakos [6] for Sandia D and F Flames. The results were very good for Sandia D Flame, however, application of the same settings to Sandia F Flame resulted in underprediction of the extent of local extinction. The LES with steady flamelet for Sandia D was also exploited by Kempf et al. [7] to study the structure of a diffusion flame in terms of length scales, scalar dissipation and flame orientation. A new premixed flamelet approach based on two additional equations for the mixture fraction and for the progress variable was proposed by Vreman et al. [8]. This in principle universal concept was validated on both premixed preheated Bunsen flame and non-premixed Sandia Flame D. The flamelet/progress variable model was also applied by Ihme and Pitsch [9,10] and used to predict extinction and reignition in Sandia Flames D and E. The concept of Steiner and Bushe [3] of the Conditional Source-term Estimation (CSE) was again applied by Ferraris and Wen [11] with some modifications reducing the number of flamelets and again validated on Sandia D. The models based on LES and transported PDF/FDF approach were also applied and validated using this flame. One of the first woks of this type was proposed by Sheikhi et. al. [12]. Bisetti and Chen [13] tested various mixing models using LES and Eulerian PDF method. Jones and Prasad [14] performed calculations for Sandia Flame D,E and F with LES and the Eulerian stochastic field method showing ability of the model to reproduce local extinction and reignition

Within the current Application Challenge attention is focused on the LES calculation only and neither RANS nor URANS predictions are analyzed.

Flow Physics and Fluid Dynamics Data

---

Contributed by: Andrzej Boguslawski — Technical University of Częstochowa

Front Page

Description

Test Data

CFD Simulations

Evaluation

Best Practice Advice

© copyright ERCOFTAC 2024