Test Data AC3-01
Buoyancy-opposed wall jet
Application Challenge 3-01 © copyright ERCOFTAC 2004
Overview of Tests
Flow loop and test section
Figure 2 and 3 show the general arrangement of the flow circuit, the measurement systems and the test section used in the present study. The flow circuit consisted of a tank from which two separate streams of water could be pumped to the test section: one through an electrical immersion heater unit having a power rating of up to 108 kW, and the other through a shell and tube heat exchanger capable of removing that amount of heat using water at 25oC from the laboratory cooling system. Each stream passed through a flow control valve and an orifice plate flowmeter. A review of the experimental rig setup can be found in paragraph 1.4 of this report.
Considerable attention was devoted to conditioning the jet flow and the background flow. For the jet flow, a hydrodynamic development section of length 600mm, about 33 times the jet gap, was provided to enable a fully developed flow condition to be achieved at the jet exit. The flow conditioning unit for the background stream at the bottom of the test section consisted of a number of graded perforated plates, a honeycomb flow straightener and multiple layers of mesh. A reasonably uniform velocity distribution was achieved by this means.
PIV system
An optical arrangement for Particle Image Velocimetry of the kind shown in Figure 2 was used for visualising the flow field. This utilised a 4 Watt Argon-ion laser as its light source. The beam was brought to the side of the test section by means of a mirror and lens arrangement, where it encountered a chopper. It was then converted into a light sheet of thickness 1.5 mm and width 600 mm, using a cylindrical glass rod. The light passed through the test section mid-way between the temperature and velocity measurement planes shown in Figure 3. Two different image recording methods were available. The first utilised a CCD camera connected to an image grabber card on a personal computer. With this arrangement, Digital Particle Velocimetry measurements could be made, but only over a limited region of the flow field. The second method utilised a film camera in conjunction with a 35 mm film scanner. This enabled the whole flow field to be studied.
LDA system
For Laser Doppler Anemometry, a two-colour, two-component system of the kind shown in Figure 2 was used in the back scatter mode. This incorporated a fibre optic probe and two burst spectrum analysers. The probe was mounted on a precision traversing mechanism which enabled the measurement volume to be accurately located at any chosen location within the flow field. The beams were introduced through the side of the test section as shown in Figure 3 and arranged so that velocities were measured in directions at angles of ±45o to the vertical. The vertical and horizontal velocity components were obtained by making a simple transformation at the data processing stage. The size of the probe volume was 0.122 mm x 0.122 mm x 8.526 mm, the longest dimension being in the z-direction, in which the mean flow was very uniform.
Temperature measuring system
Thermocouples were used for mapping the temperature field. The distribution of temperature along the jet wall was measured using eleven fixed thermocouples with the junctions situated in the water quite near to the wall surface; wall temperatures were not measured directly. The distribution of temperature over the whole flow field was measured in the mid plane of the test section using a motor driven, traversable rake carrying twenty one ‘fast response’ thermocouple junctions, made of wire of diameter only 0.076 mm. As shown in Figure 2, the thermocouple signals were supplied to a 60 channel, computer-based scanning system connected to a precision, digital voltmeter controlled by a micro-processor.
Experimental conditions
Reynolds number and Richardson number were both varied in the experiments reported here. This was done by controlling the velocities of the jet flow and the background flow and their temperatures. The mean velocity of the jet flow was varied from 0.10 m/s to 0.20 m/s and the temperature difference between the jet flow and the counter-current background flow was varied between 4oC and 10oC. As a result, the Reynolds number of the jet varied in the range 3000 to 6000 and Grashof number varied in the range 225500 to 563700. Thus the Richardson number varied from 0.010 to 0.052. The molecular viscosity and thermal expansivity of water was assumed to be that at pressure of 1 bar and at the appropriate temperature.
The experimental configuration did not permit the inlet velocity and turbulence profiles of the jet flow and the background flow to be measured. However, with regard to the jet flow, the development length from the top of the rig was about 30 channel widths. An appropriate approximation for the jet flow is consequently a fully-developed flow profile.
The fluid temperature at the jet exit was kept constant at 42oC in all experiments. This was achieved by adjusting the flow rate of the cooling water supplied to the cooler. The main parameters and experimental conditions in the experiments performed are summarised below in Table 1.
Velocity measurements
For each test case, velocity was measured using the LDA probe at a particular elevation in the vertical direction from y = -100 mm to y = 800 mm, normally in steps of 100 or 50 mm. In the mixing region between the warm jet fluid and the colder counter-current stream the steps were reduced to 20 mm.
At each elevation, between 9 to 18 measurements were made between x = 14 mm and x = 242 mm, mostly at intervals of 25.4 mm except in the region near the edge of the jet flow where the steps were reduced to 5 mm.
LDA signals were collected for about 5 minutes. Due to the velocity being low the data collection rate was quite low. For isothermal conditions, it varied from 15Hz to 40Hz. For non-isothermal conditions, it was even lower (6Hz to 15Hz) due to the influence of variations of refractive index in the water. The estimated accuracy of the LDA velocity measurements was 1 to 2%.
| Test | Re | Gr | Ri | Vc/Vj | Mj(kg/s) | Mc(kg/s) | Tj(°C) | Tc(°C) |
|---|---|---|---|---|---|---|---|---|
| 1 | 3000 | 0 | 2.27 | 0 | 42 | |||
| 2 | 3000 | 0.077 | 2.27 | 2.9 | 42 | 42 | ||
| 3 | 4000 | 0 | 3.03 | 0 | 42 | |||
| 4 | 4000 | 0.077 | 3.03 | 3.88 | 42 | 42 | ||
| 5 | 4754 | 0 | 3.6 | 0 | 42 | |||
| 6 | 4754 | 0.077 | 3.6 | 4.62 | 42 | 42 | ||
| 7 | 4754 | 234056 | 0.01 | 0.077 | 3.6 | 4.62 | 42 | 38 |
| 8 | 6000 | 468113 | 0.013 | 0.077 | 4.54 | 5.83 | 42 | 34 |
| 9 | 4754 | 468113 | 0.02 | 0.077 | 3.6 | 4.62 | 42 | 34 |
| 10 | 4754 | 585142 | 0.026 | 0.077 | 3.6 | 4.62 | 42 | 32 |
| 11 | 4000 | 468113 | 0.029 | 0.077 | 3.03 | 3.88 | 42 | 34 |
| 12 | 3000 | 468113 | 0.052 | 0.077 | 2.27 | 2.9 | 42 | 34 |
| 13 | 4000 | 0.15 | 3.03 | 7.54 | 42 | 34 | ||
| 14 | 4000 | 0.15 | 3.03 | 7.54 | 42 | 42 |
Temperature measurements
The rake used for temperature measurements had 21 thermocouples on it equally spaced across the field from x = 59 mm to x = 296 mm. The rake could be moved by a stepper motor under the control of the computer so that the data could be collected automatically.
Two data acquisition modes were available, one fast and one slow. The former was used to obtain time mean measurements over a long period of time and the latter was used to study the variation of temperature with time.
To obtain the distribution of mean temperature over the whole field, the rake was traversed from y = -100 mm in steps of 100 or 50 mm. In the mixing region the steps were reduced to either 20 or 10 mm. At each station, all the thermocouples (including those attached to the wall) were scanned in the slow mode 100 times over a period of 20 minutes to enable mean values of temperature to be obtained.
Measurements of local temperature variation with time were obtained using five selected thermocouples on the rake. Those selected were at locations x = 59 mm, 108 mm, 168 mm, 227 mm and 296 mm. For these measurements, the fast mode of data acquisition was selected to sample 5000 times for each point in 5 minutes. Such measurements were made a stations from y = -100 mm to y = 700 mm, in steps of 100 or 50 mm. In the mixing region the steps were reduced to 20 mm.
Precision on all temperature measurements is +/- 0.3 oC and all measured data are available in digital form.
Results
Figure 4 (a) to (d) and Figure 5 (a) to (f) show mean flow velocity vector fields for isothermal and non-isothermal flow with and without an ascending stream. Jet Reynolds numbers of 3000 and 4754 were used in these experiments. For the experiments with an ascending stream, the ratio of the jet flow velocity to the ascending flow velocity was kept constant at =0.077. The flow pattern is similar for the two jet Reynolds numbers. The jet penetration distance is reduced by the presence of the ascending stream to about 0.6m for isothermal flow and to as little as 0.1 m for non-isothermal flows, depending on the strength of buoyancy.
Figure 6 (a) to (f) shows temperature fields for different Richardson numbers. As also shown by the LDA plots of Figure 5, as the Richardson number increases the influence of buoyancy increases too, resulting in much smaller mixing regions. A direct consequence of the contraction of the extent of the mixing region is the reduction of the penetration length.
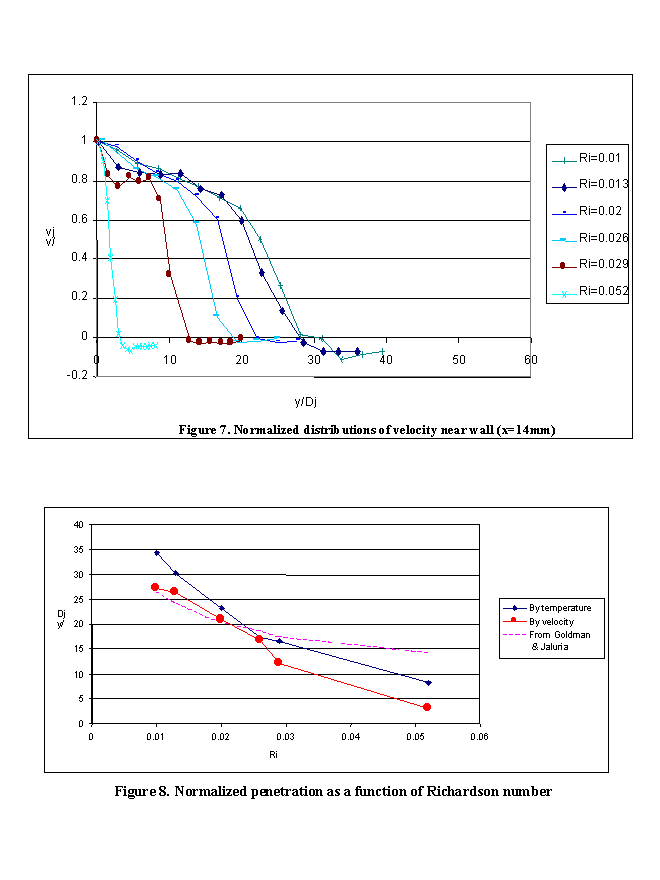
Figure 7 shows the variation of normalised downward velocity with height at a distance 14 mm from the jet wall for various values of Richardson number. Three stages can be identified. Immediately below the jet exit there is a development region where the velocity decays relatively slowly. Further down, at a distance depending on Richardson number, the decay of velocity becomes greater due to mixing. Eventually the value becomes negative, indicating that the region of the counter-current flow has been reached. It is clear that the greater the buoyancy influence, the earlier the velocity variation departs from the first stage. It can also been seen that the higher the Richardson number, the steeper is the velocity variation within the mixing region and the shorter the region is. It is interesting to note that, for the cases 0.026, the values of velocity within the wall jet development region seem to collapse onto the same curve indicating that the flow was affected little by buoyancy.
Figure 8 shows the variation of normalised jet penetration distance with Richardson number determined from measurements of the temperature field. Penetration is defined rather arbitrarily as the distance from the jet exit to the location at which the normalised wall temperature falls to about a value of 0.02.
Figures 9 and 10 show the effects of velocity ratio for isothermal and non-isothermal flows respectively, by comparing plots of the mean and fluctuating velocity fields and for the non-isothermal velocity also the temperature fields for velocity ratios of 0.077 (also shown in earlier plots) and 0.15. It should be noted that the values of the measured turbulent kinetic energy, , are based on measurements of two of the three components of the turbulent intensity, namely those along the vertical and the horizontal cross-channel directions. Starting with the isothermal case in Figure 9, the effective doubling of the up-flow velocity appears to reduce the penetration length by a factor of about four. The maximum level is not significantly affected, but the higher up-flow severely limits the size of the high region. The non-isothermal comparisons in Figure 10 show that while the increase in up-flow again reduces the penetration length, this reduction is not as strong as in the isothermal case. On the other hand, the increase in up-flow now also limits the spreading of the jet across the channel more markedly than in the isothermal case.
© copyright ERCOFTAC 2004
Contributors: Jeremy Noyce - Magnox Electric
Site Design and Implementation: Atkins and UniS