Evaluation AC7-03
Flow in a Ventricular Assist Device - Pump Performance & Blood Damage Prediction
Application Challenge AC7-03 © copyright ERCOFTAC 2022
Evaluation
Experimental Validation of URANS and LES
For simulations in turbopumps, hydraulic characteristics such as the head are among the most important result variables. Also in the field of CFD applications in VADs, it is common to use the head to validate the numerical calculation. In fact, the measurement of the head is the only experimental validation of the simulated flow field in a large number of literature studies (e.g., in [4], [5], [28], [29]). Since the pressure in the pump is coupled via the governing equations to the flow field, the comparison of the heads can be used as the first stage of flow field validation in VADs.
The experimental and numerical results are given in Figure 5.1. For the operating point at , good agreement between numerical and experimental results can be observed with a deviation of for LES and for URANS. For the smaller flow rate the deviations are slightly larger with for LES and for URANS.
In summary, the discrepancy between numerically and experimentally determined head is still within an acceptable range for both LES and URANS. From this, it can be concluded that both numerical models are valid for reproducing the real pressure buildup of the VAD.
Fluid Mechanical & Hemodynamical Evaluation of LES and URANS
Inner Efficiencies
The inner efficiencies according to Eq. (2) of the impeller (index: ) and the whole pump (index: ) are given in Tab. 5.1. The deviation between the URANS and the reference LES case are minor for both operation points with a maximum deviation of . It can be concluded that the turbulence-modelling URANS method can reflect the efficiencies, and hence the global losses, as accurately as the turbulence-resolving LES method.
| Flow Rate | Parameter | LES | URANS | Relative deviation to LES [%] |
|---|---|---|---|---|
Effective Stresses in the time-averaged flow field
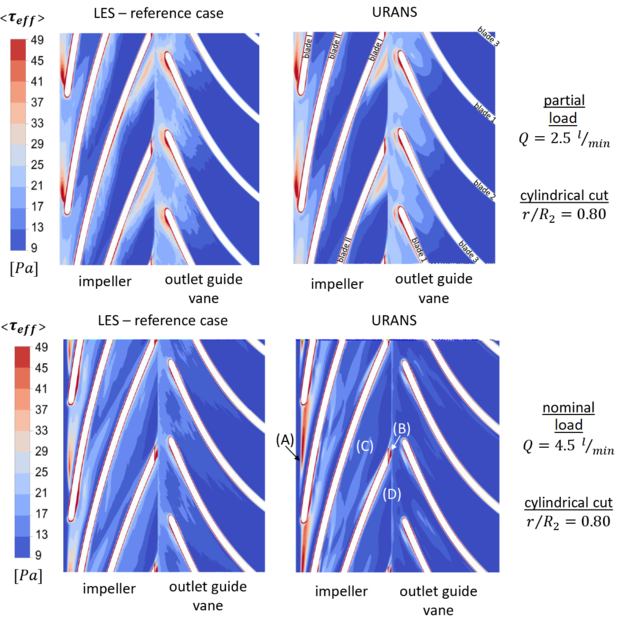
The computed effective stresses (Eq. (10) in section Description) are presented for both operating points in Fig. 5.2. The stresses from the reference LES are compared to the URANS computations (The instantaneous, effective stresses are dispalyed in Fig. 1.3 in section Description). As can be seen from the LES results, relevant stresses above 9 Pa (threshold for vWF degradation) and 50 Pa (platelet activation) are present within the flow channel of the rotor and the outlet guide vane. In general, the stresses are underpredicted with URANS. Nevertheless, similar hot-spots for significant stresses are observable for the partial load (). This is in contrast to the nominal operation point (), where greater deviations in computed stresses are noticable between LES and URANS. Despite the fact that the URANS can reflect the high stresses in the gap vortex and the trailing edge flow regions (red areas marked with (A) and (B)), other relevant regions in the blade channels of the impeller (C) or in the area between the impeller and the outlet guide vane (D) cannot be reflected adequately for the nominal operation point. In these areas of the pump, complex interactions occur between secondary flows are present (explained in Refs. [2] and [27]), which are resolved directly by the LES. In contrast, the URANS turbulence model cannot model the impact of these complex turbulent flow interactions on the effective stress field adequately .
Hemodynamical Evaluation: Hemolysis Index and Volumetric Threshold Analysis
The computed MIH indices (defined by Eq. (12) in section Description) are shown in Table 5.2. As already displayed in the stress fields in Fig. 5.2., the LES computes higher hemolysis values thans URANS in both operating points. This is partly due to the coarser spatial and temporal resolution of the stresses in URANS (also recognizable from the grid convergence study in Fig. 3.3 in section CFD Simulations). But also the already mentioned insufficient resolution of the secondary structures in the blade channels leads to the larger deviations at at .
| by Eq. (12) | partial load | nominal load |
|---|---|---|
| LES - reference | ||
| URANS |
Tables 5.3. and 5.4. show the percentage of the entire VAD volume in which certain stress thresholds for van-Willebrand-degradation (vWF; ), platelet activation () and hemolysis () are exceeded. Again, the computed results of URANS are lower than those from LES. Relative deviations of maximal () are observable for the stress thresholds of and . Only for the stress threshold above , larger deviations are present for both URANS cases, which is due to the coarser near-wall grid density, where the highest stresses are present. These near-wall stresses affect the numerical hemolysis prediction greatly (see Ref. [29] or [31]).
As can be seen from these hemodynamic results, the discrepancies between URANS and LES in the evaluation of blood damage are many times greater than those for the previously evaluated fluid mechanical parameters such as head or efficiency.
| LES - reference | |||
| URANS |
| LES - reference | |||
| URANS |
Contributed by: B. Torner — University of Rostock, Germany
© copyright ERCOFTAC 2022













![{\displaystyle \eta _{i,i}~[\%]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/149f79f65f0cdbc360f827910bdc493f73b58ab8)






![{\displaystyle \eta _{i,p}~[\%]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/411e8106f44cbef20d2d35a730e0063a16320115)











![{\displaystyle {MIH}~[-]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ed1a4a3a15aca42d55d3dd000370bdd40d359de)













![{\displaystyle I_{\tau _{eff}>9~Pa}~[\%]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/aca0a3d2898581851afd6da764e5d1d5a61dcb78)
![{\displaystyle I_{\tau _{eff}>50~Pa}~[\%]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c83af4cdc77065d07063238c073072f223569397)
![{\displaystyle I_{\tau _{eff}>150~Pa}~[\%]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8a1cf8e564ceba2182e9d25106615ae457800f11)











