UFR 4-08 Test Case
Orifice/deflector flow
Underlying Flow Regime 4-08 © copyright ERCOFTAC 2004
Test Case
Brief description of the study test case
The present case considers the flow through a sharp-edged orifice mounted into a tube of D = 50 mm (± 0.02 mm) inner diameter (Fig. 5). Two geometries of the orifice were used for the experiments and the numerical computations summarised in Table 1. The two cases differ only in the thickness of the orifice plate while all other geometrical parameters were identical. Water as well as a mixture of different Diesel oils were used as working fluids. Their properties are provided in Table 2. The flow Reynolds number was 13,000 (water) and 22,000 (Diesel oil) for the case A and for the case B also 22,000. The measured quantities which can be used to assess the quality of the computations are profiles in front and behind the orifice for the stream-wise and radial mean velocities as well as all fluctuating components. Moreover, profiles of the Reynolds stresses ![]() and
and ![]() were measured. As integral properties, the re-attachment length and the wall friction coefficient are presented.
were measured. As integral properties, the re-attachment length and the wall friction coefficient are presented.
Fig. 5 Geometry of the flow through a sharp-edged orifice Studied by Wang (2001)
|
Test case |
D/d |
L/H |
L/d |
Re (liquid) |
|
A |
2.0 |
2.0 |
1.0 |
Re = 13000 (water) Re = 22000 (Diesel Oil) |
|
B |
2.0 |
0.08 |
0.04 |
Re = 22000 (Diesel Oil) |
Table 1 Dimensions of the orifice plate mounted in a pipe of inner diameter D = 50 mm and pipe Reynolds number
|
Liquid |
Density [kg/m3] |
Kinematic Viscosity [m2/s] |
Temperature |
|
Water |
1000 |
1.0 × 10-6 |
20°C |
|
Diesel Oil |
836 |
2.692 × 10-6 |
20°C |
Table 2 Liquid properties
Test Case Experiments
The experimental studies were performed in a closed-loop pipe flow system also described by Durst & Wang (1989). The test section of 1 m length was mounted in the horizontal pipe section in such a way that the inflow length of the pipe was 60 D (i.e. the horizontal pipe upstream the orifice) and the outflow length of the pipe was 36 D. This configuration ensured a fully developed flow at the entrance to the test section. The velocity measurements were performed by a single component Laser-Doppler anemometer which could be rotated to have access to all the velocity components. In order to minimize the refraction of the light at the curved pipe wall, the test section was placed in a square container also filled with the test liquid. Especially for the Diesel oil mixture a full refractive index matching could be achieved by properly adjusting the liquid temperature. Details of the geometry of the orifice plate also made of quartz glass are provide in Table 1 (see also Fig. 5) and the properties of the process liquids are given in Table 2. Measured velocity profiles (all three mean and rms velocities and two Reynolds stresses) are available at the following normalized axial locations (x/H) with respect to the center of the orifice plate: -4.0, -0.8, -0.5, 0.5, 0.8, 2.0, 4.0, 6.0, 8.0, 10.0, 12.0, 16.0 and 28.0. The re-attachment length was obtained by interpolating the velocity measurements (stream-wise component) at several stream-wise coordinates around the stagnation point. An extrapolation to the wall was possible by doing this for several wall distances.
The following measurement accuracies were identified:
LDA:
relative deviation < 1 % (typically for 20,000 samples at each measurement location)
Traversing system:
Stream-wise direction: ± 0.25 mm
Positioning in the cross-section of the pipe: ± 10 μm
Temperature regulation:
± 0.5°C
The symmetry of the flow was proven for several stream-wise cross-sections.
CFD Methods
The numerical computations were performed for an axi-symmetric, incompressible and stationary turbulent flow. The Reynolds-averaged conservation equations were closed by applying the standard k-ε turbulence model. The basis of the computations was the in-house code CAST (Peric and Scheuerer, 1989), which uses a finite-volume approach. A non-equidistant regular grid was used with a strong refinement in the vicinity of the orifice. With the aid of a multi-grid approach, the convergence behavior was accelerated. The diffusive terms were discretised by 2nd order central differences, while the convective terms were discretised based on flux-blending, i.e. combining 50 % upwind and 50 % central differencing. Pressure-velocity coupling was solved iteratively using the SIMPLE-algorithm.
The boundary conditions for the computations were as follows:
- The inlet conditions were specified according to the measured profiles of mean velocities and the turbulent kinetic energy.
- The profile of the dissipation rate was estimated from the ratio k3/2/lm. The mixing length lm was obtained from a computation for a developed pipe flow and scaled in such a way to yield reasonable good agreement with the profiles of the measured mean velocities and turbulent kinetic energy downstream of the orifice.
- Symmetry conditions on the pipe axis.
- Gradient-free conditions at the outlet.
- The wall was treated with no-slip conditions and wall functions were used for the wall-nearest control volume.
The grid independence of the results was analyzed for a number of different grid resolutions (i.e. 62 x 14, 62 x 28, 124 x 28, 124 x 56 and 248 x 56). For this purpose profiles of the velocities, the turbulent kinetic energy and the re-attachment length were considered. For the three finest grids the re-attachment length closely approached the measured value. The difference was only 0.5 % (Fig. 6).
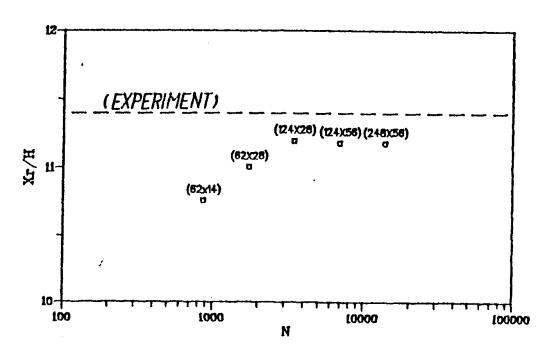
Fig. 6 Comparison of the normalised re-attachment length calculated with different grid resolution with the measured value for case B Wang (2001)
The solution errors were estimated using Richardson expansions. For the stream-wise velocity component the solution errors were smaller than 1 % in the bulk of the flow and in the region of the orifice and the re-attachment less than 5 %. The solution errors for the other velocity components and the turbulent kinetic energy were found to be smaller than 0.2 %.
© copyright ERCOFTAC 2004
Contributors: Martin Sommerfeld - Martin-Luther-Universitat Halle-Wittenberg
