UFR 3-35 Evaluation: Difference between revisions
No edit summary |
|||
| (42 intermediate revisions by 3 users not shown) | |||
| Line 4: | Line 4: | ||
|number=35 | |number=35 | ||
}} | }} | ||
__TOC__ | |||
= Evaluation = | = Evaluation = | ||
For the evaluation of the numerical and experimental data sets in the symmetry plane upstream of a wall-mounted cylinder the following quantities are presented: | For the evaluation of the numerical and experimental data sets in the symmetry plane upstream of a wall-mounted cylinder the following quantities are presented: | ||
| Line 19: | Line 18: | ||
== Streamlines == | == Streamlines == | ||
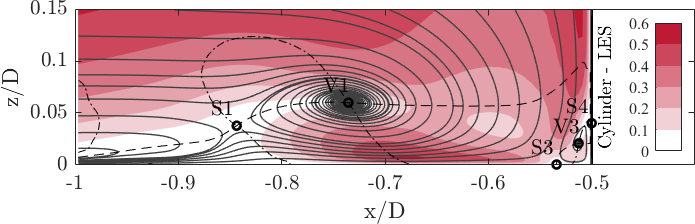
The streamlines of the PIV and the LES data agree well according to Fig. 6. The plots are | The streamlines of the PIV and the LES data agree well according to Fig. 6. The plots are coloured by the normalized magnitude of the velocity in the symmetry plane, <math> ||\vec{U}|| = \sqrt{\langle u^2\rangle + \langle w^2\rangle}/u_{\mathrm{b}}</math>. The dashed and dash-dotted lines indicate the zero-isoline of the streamwise and vertical velocity component, respectively. | ||
The approaching turbulent boundary layer is redirected downwards at the flow facing edge of the cylinder caused by a vertical pressure gradient. This downflow reaches the bottom plate of the flume at the stagnation point S3. Here, it is redirected (i) in the out-of-plane direction bending around the cylinder; (ii) towards the cylinder rolling up and forming the corner vortex V3; and (iii) in the upstream direction accelerating and forming a wall-parallel jet. The jet accelerates and exerts a large wall-shear stress on the bottom plate (see Fig. 22). Parts of the downflow form the horseshoe vortex V1. Upstream of this vortex system, the approaching flow is blocked and causes a saddle point S1 with zero velocity magnitude. | The approaching turbulent boundary layer is redirected downwards at the flow facing edge of the cylinder caused by a vertical pressure gradient. This downflow reaches the bottom plate of the flume at the stagnation point S3. Here, it is redirected (i) in the out-of-plane direction bending around the cylinder; (ii) towards the cylinder rolling up and forming the corner vortex V3; and (iii) in the upstream direction accelerating and forming a wall-parallel jet. The jet accelerates and exerts a large wall-shear stress on the bottom plate (see Fig. 22). Parts of the downflow form the horseshoe vortex V1. Upstream of this vortex system, the approaching flow is blocked and causes a saddle point S1 with zero velocity magnitude. | ||
[[File:UFR3-35_PIV_streamlines_mag.png|centre|frame|Fig. 6 a) Streamlines of time-averaged flow field | [[File:UFR3-35_PIV_streamlines_mag.png|centre|frame|Fig. 6 a) Streamlines of time-averaged flow field coloured by the in-plane velocity magnitude <math> ||\vec{U}_{\mathrm{PIV}}|| = \sqrt{\langle u^2\rangle + \langle w^2\rangle}/u_{\mathrm{b}}</math> ]]. | ||
[[File:UFR3-35_LES_streamlines_mag.png|centre|frame|Fig. 6 b) Streamlines of time-averaged flow field | [[File:UFR3-35_LES_streamlines_mag.png|centre|frame|Fig. 6 b) Streamlines of time-averaged flow field coloured by the in-plane velocity magnitude <math> ||\vec{U}_{\mathrm{LES}}|| = \sqrt{\langle u^2\rangle + \langle w^2\rangle}/u_{\mathrm{b}}</math> ]]. | ||
== Location of the | == Location of the critical points == | ||
The position of the characteristic flow structures highlighted in the streamline plots is listed in the following table | The position of the characteristic flow structures highlighted in the streamline plots is listed in the following table | ||
| Line 84: | Line 83: | ||
[[File:UFR3-35_position_of_profiles.png|thumb|centre|550px|Fig. 7: Position of vertical profiles in the flow]] | [[File:UFR3-35_position_of_profiles.png|thumb|centre|550px|Fig. 7: Position of vertical profiles in the flow]] | ||
Since the | Since the positions of the horseshoe vortex in the LES and the PIV are slightly different, we use an adjusted <math> x-</math>coordinate, in order to compare the data at the same position in the flow. The coordinate is defined as follows (Schanderl 2018): | ||
<math>x_{\mathrm{adj}} = \frac{x - x_{\mathrm{Cyl}}}{x_{\mathrm{Cyl}} - x_{\mathrm{V1}}}</math>, | <math>x_{\mathrm{adj}} = \frac{x - x_{\mathrm{Cyl}}}{x_{\mathrm{Cyl}} - x_{\mathrm{V1}}}</math>, | ||
| Line 91: | Line 90: | ||
[[File:UFR3-35_U_z.png|centre| | [[File:UFR3-35_U_z.png|thumb|centre|800px|Fig. 8: Vertical profiles of the streamwise velocity component <math> \langle u(z)\rangle /u_{\mathrm{b}}</math> ]] | ||
The vertical | |||
The vertical profiles of the streamwise velocity <math> u(z) </math> are presented at the selected locations in Fig. 8. The wall-parallel jet starts to develop from S3 onward and the flow accelerates. At <math>x_{\mathrm{adj}} = -0.25 </math>, a near-wall velocity peak appears, which becomes more pronounced in the upstream direction (see <math>x_{\mathrm{adj}} = -0.5 </math>). In this region, the wall-shear stress reaches on the one hand its maximum value and on the other hand reveals a plateau-like shape (this is shown and discussed later, see Fig. 22). This means that the largest values of the gradient <math>\frac{\partial \langle u \rangle}{\partial z}</math> appear. Underneath the horseshoe vortex, the reverse flow decelerates and the near-wall-peak of the velocity lifts from the bottom plate and becomes less distinct. Further upstream, the near-wall peak of the streamwise velocity disappears as the wall-parallel jet fades out. | |||
Due to the evaluation of the PIV images by an interrogation-window-based cross correlation, the strong gradient <math>\frac{\partial \langle u \rangle}{\partial z}</math> at the wall cannot be fully resolved, and therefore, the near-wall peak of the streamwise velocity is damped in the experimental data. | Due to the evaluation of the PIV images by an interrogation-window-based cross correlation, the strong gradient <math>\frac{\partial \langle u \rangle}{\partial z}</math> at the wall cannot be fully resolved, and therefore, the near-wall peak of the streamwise velocity is damped in the experimental data. | ||
[[File:UFR3- | [[File:UFR3-35_uu_z.png|thumb|centre|800px|Fig. 9 a) Vertical profiles of the Reynolds normal stress <math> \langle u'u'(z)\rangle/u_{\mathrm{b}}^2</math> ]] | ||
[[File:UFR3-35_uw_z.png|thumb|centre|800px|Fig. 9 b) Vertical profiles of the Reynolds shear stress <math> \langle u'w'(z)\rangle/u_{\mathrm{b}}^2</math> ]] | |||
[[File:UFR3-35_k_z.png|thumb|centre|800px|Fig. 9 c) Vertical profiles of the inplane turbulent kinetic energy <math> \langle k(z)\rangle = 0.5(\langle u'^2\rangle+\langle w'^2\rangle)/u_{\mathrm{b}}^2</math>]] | |||
The vertical profiles of the Reynolds normal stress <math> \langle u'u'\rangle </math>, the Reynolds shear stress <math> \langle u'w'\rangle </math> and the resulting turbulent kinetic energy <math> \langle k\rangle </math> comprising only streamwise and vertical fluctuating velocity components (inplane with respect to the symmetry plane) are presented in Fig. 9a) to c), respectively. Note, that the range of the <math>x-</math>axis is not constant for the sake of better visibility. The experimental and numerical data agree reasonably well both with regard to amplitude and shape. Again, the quality of the PIV data near the wall is undermined by the strong gradients being evaluated using interrogation windows. | |||
The largest values of <math>\langle u'u'\rangle</math> are found underneath the horseshoe vortex. This is the foot of the c-shaped distribution of the turbulent kinetic energy. In the wall jet at <math>x_{\mathrm{adj}} = -0.25 </math> and <math> -0.5 </math> the Reynolds stresses are generally small which is explained by the fact that the wall jet is strongly accelerated in upstream direction which leads to a negative production term in the turbulent kinetic energy balance (see next section). Large Reynolds shear stress can be found between the horseshoe vortex and the stagnation point S1 at <math>x_{\mathrm{adj}} ~ -1.5 </math>. Large values of the turbulent kinetic energy can be found around the horseshoe vortex center (due to large <math> \langle w'w'\rangle </math>) and under the horseshoe vortex near the wall (due to <math> \langle u'u'\rangle </math>). | |||
There is a specific issue interesting for modeling. In the lower region of the wall jet (between the velocity maximum of the wall jet and the wall) the Reynolds shear stress does not change sign as does the vertical velocity gradient and hence does not follow the eddy viscosity hypothesis. This is due to the complex flow and turbulence behaviour in this region. Consequently, eddy-viscosity models would have difficulties to reproduce the near-wall shear-stress distribution. | |||
[[File:UFR3-35_W_x_V1.png|centre|frame|Fig. 10: Horizontal profiles of the vertical velocity component <math> \langle w(x)\rangle/u_{\mathrm{b}}</math> at the height <math> z_{\mathrm{V1}}/D</math>]] | [[File:UFR3-35_W_x_V1.png|centre|frame|Fig. 10: Horizontal profiles of the vertical velocity component <math> \langle w(x)\rangle/u_{\mathrm{b}}</math> at the height <math> z_{\mathrm{V1}}/D</math>]] | ||
Analysing the profile of the vertical velocity component <math>\langle w(x)\rangle </math> along the <math> x-</math>axis at the height of the horseshoe vortex (see Fig. 10), reveals on the one hand the clockwise rotation of the vortex, and on the other hand two minima between the horseshoe vortex and the cylinder. At <math>x_{\mathrm{adj}} \approx -0.1 </math>, the peak in the downwards directed flow stems from the downflow, while the second local minimum at approximately <math>x_{\mathrm{adj}} = -0.65 </math> represents the downwards rotation of the horseshoe vortex. | Analysing the profile of the vertical velocity component <math>\langle w(x)\rangle </math> along the <math> x-</math>axis at the height of the horseshoe vortex (see Fig. 10), reveals on the one hand the clockwise rotation of the vortex, and on the other hand two minima between the horseshoe vortex and the cylinder. At <math>x_{\mathrm{adj}} \approx -0.1 </math>, the peak in the downwards directed flow stems from the downflow along the cylinder front face, while the second local minimum at approximately <math>x_{\mathrm{adj}} = -0.65 </math> represents the downwards rotation of the horseshoe vortex. | ||
Both data sets agree well in shape. However, the LES data indicate higher amplitudes in general, as the stagnation point at the cylinder front at which the approach flow is deflected and | Both data sets agree well in shape. However, the LES data indicate higher amplitudes in general, as the stagnation point at the cylinder front at which the approach flow is deflected and the downflow evolves, is located at the water level in the LES. On the other hand it was shifted downwards in our experiment, due to the plate of acrylic glass placed at the water surface. This is, however, not an artefact as a bow wave (surface roller) would evolve in this area if this plate were not present according to e.g. Melville 2008. Therefore, the downwards deflected part of the flow is smaller in the experiment and hence the HV system becomes smaller too. | ||
[[File:UFR3-35_uiuj_x_V1.png|centre|frame|Fig. 11: Horizontal profiles of the Reynolds stresses <math> \langle u_i'u_j'(x)\rangle/u_{\mathrm{b}}^2</math> and the turbulent kinetic energy <math> \langle k(x)\rangle = 0.5(\langle u'^2\rangle+\langle w'^2\rangle)/u_{\mathrm{b}}^2</math> at the height <math> z_{\mathrm{V1}}/D</math>]] | [[File:UFR3-35_uiuj_x_V1.png|centre|frame|Fig. 11: Horizontal profiles of the Reynolds stresses <math> \langle u_i'u_j'(x)\rangle/u_{\mathrm{b}}^2</math> and the turbulent kinetic energy <math> \langle k(x)\rangle = 0.5(\langle u'^2\rangle+\langle w'^2\rangle)/u_{\mathrm{b}}^2</math> at the height <math> z_{\mathrm{V1}}/D</math>]] | ||
Distributions of the Reynolds stresses <math>\langle u_i'u_j'\rangle</math> and the inplane turbulent kinetic energy <math>\langle k\rangle</math> at the height of the horseshoe vortex are shown in Fig. 11 and reveal similar distributions for the PIV and LES results. At the centre of the vortex, the normal stresses, and consequently the turbulent kinetic energy as well, reveal a peak, which wears off in the up- and downstream direction. In addition, the downflow close to the cylinder surface generates stresses as well. | |||
The shear stress plays a minor role in the region between the cylinder and the horseshoe vortex, while it becomes negative upstream of the horseshoe vortex indicating the interference of the approaching flow with the horseshoe vortex. | The shear stress plays a minor role in the region between the cylinder and the horseshoe vortex, while it becomes negative upstream of the horseshoe vortex indicating the interference of the approaching flow with the horseshoe vortex. | ||
| Line 122: | Line 131: | ||
The spatial distribution of the time-averaged in-plane turbulent kinetic energy <math> \langle k \rangle = 0.5(\langle u'^2\rangle+\langle w'^2\rangle)/u_{\mathrm{b}}^2</math> reveals on the one hand the well-known c-shaped structure (e.g. Paik 2007) with the largest amplitude at the centre of the horseshoe vortex stemming from vertical fluctuations induced by the horizontal oscillations of the horseshoe vortex (see Fig. 12 a) and b). The lower branch of the c-shape contains mainly streamwise (horizontal) fluctuations linked to the dynamics of the wall-parallel jet. On the other hand, the experimental and numerical data sets show high similarity and agree well with each other, as the peak amplitude is approximately the same: <math> \langle k_{\mathrm{PIV, inplane}}\rangle = 0.074u_{\mathrm{b}}^2</math>; <math> \langle k_{\mathrm{LES, inplane}}\rangle = 0.079u_{\mathrm{b}}^2</math>. The black circle marks the centre of the horseshoe vortex. | The spatial distribution of the time-averaged in-plane turbulent kinetic energy <math> \langle k \rangle = 0.5(\langle u'^2\rangle+\langle w'^2\rangle)/u_{\mathrm{b}}^2</math> reveals on the one hand the well-known c-shaped structure (e.g. Paik 2007) with the largest amplitude at the centre of the horseshoe vortex stemming from vertical fluctuations induced by the horizontal oscillations of the horseshoe vortex (see Fig. 12 a) and b). The lower branch of the c-shape contains mainly streamwise (horizontal) fluctuations linked to the dynamics of the wall-parallel jet. On the other hand, the experimental and numerical data sets show high similarity and agree well with each other, as the peak amplitude is approximately the same: <math> \langle k_{\mathrm{PIV, inplane}}\rangle = 0.074u_{\mathrm{b}}^2</math>; <math> \langle k_{\mathrm{LES, inplane}}\rangle = 0.079u_{\mathrm{b}}^2</math>. The black circle marks the centre of the horseshoe vortex. | ||
When the fluctutuations of the three dimensional velocity vector | When the fluctutuations of the three-dimensional velocity vector are used to determine the turbulent kinetic energy <math> \langle k_{\mathrm{LES, total}}\rangle = 0.5(\langle u'^2\rangle+\langle v'^2\rangle+\langle w'^2\rangle)/u_{\mathrm{b}}^2</math>, the additional out-of-plane component does not change the shape of the distribution (see Fig. 12 c). However, the amplitudes at the horseshoe vortex centre and inside the lower branch of the c-shape both increase due to the vortex bending around the cylinder entailing increased out-of-plane fluctuations, e.g. at V1: <math> \langle k_{\mathrm{LES, total}}\rangle = 0.09u_{\mathrm{b}}^2</math>. | ||
The budget equation of the turbulent kinetic energy reads | The budget equation of the turbulent kinetic energy reads: | ||
<math> 0 = P + \nabla T - \epsilon + C </math>, | <math> 0 = P + \nabla T - \epsilon + C </math>, | ||
| Line 137: | Line 146: | ||
* mean convection: <math> C = - \langle u_i\rangle \frac{\partial k}{\partial x_i} </math> (steady state) | * mean convection: <math> C = - \langle u_i\rangle \frac{\partial k}{\partial x_i} </math> (steady state) | ||
The individual terms of the budget equation of the TKE are normalized by <math> D/u_{\mathrm{b}}^3</math> and presented in the following | The individual terms of the budget equation of the TKE are normalized by <math> D/u_{\mathrm{b}}^3</math> and presented in the following subsections. | ||
=== Production of turbulent kinetic energy === | === Production of turbulent kinetic energy === | ||
| Line 145: | Line 154: | ||
Fig. 13 a) and b) show the TKE production using the PIV and LES results, respecively. The main region of positive production of turbulent kinetic energy can be found upstream of the centre of the hoseshoe vortex (black circle) and inside the wall-parallel jet. The amplitude of both data sets is about <math> 0.3u_{\mathrm{b}}^3/D </math> in the region of the horseshoe vortex, while the LES data resolve the TKE production in the jet in more detail than the PIV data. The amplitudes here are <math> P_{\mathrm{LES}} \approx 0.4u_{\mathrm{b}}^3/D </math> and <math> P_{\mathrm{PIV}} \approx 0.2u_{\mathrm{b}}^3/D </math>. The oscillations of the horseshoe vortex are responsible for causing fluctuations, which in turn produce turbulent kinetic energy. | Fig. 13 a) and b) show the TKE production using the PIV and LES results, respecively. The main region of positive production of turbulent kinetic energy can be found upstream of the centre of the hoseshoe vortex (black circle) and inside the wall-parallel jet. The amplitude of both data sets is about <math> 0.3u_{\mathrm{b}}^3/D </math> in the region of the horseshoe vortex, while the LES data resolve the TKE production in the jet in more detail than the PIV data. The amplitudes here are <math> P_{\mathrm{LES}} \approx 0.4u_{\mathrm{b}}^3/D </math> and <math> P_{\mathrm{PIV}} \approx 0.2u_{\mathrm{b}}^3/D </math>. The oscillations of the horseshoe vortex are responsible for causing fluctuations, which in turn produce turbulent kinetic energy. | ||
From the stagnation point S3 onwards in the upstream direction, the TKE production is negative, meaning that inside the accelerating jet TKE is transferred | From the stagnation point S3 onwards in the upstream direction, the TKE production is negative, meaning that inside the accelerating jet TKE is transferred to mean kinetic energy. When the jet decelerates at about <math> x = -0.7D</math>, the jet becomes more unstable, fluctuations occur, and therefore, <math> P </math> becomes positive. | ||
=== Diffusive transport of turbulent kinetic energy === | === Diffusive transport of turbulent kinetic energy === | ||
| Line 162: | Line 170: | ||
[[File:UFR3-35_LES_T_visc.png|centre|frame|Fig. 16 Diffusive transport of turbulent kinetic energy due to viscous diffusion <math> \nabla T_{\mathrm{visc, LES}} = 2\nu\frac{\partial \langle u_j's_{ij}\rangle}{\partial x_i} \cdot D/u_{\mathrm{b}}^3 </math>]] | [[File:UFR3-35_LES_T_visc.png|centre|frame|Fig. 16 Diffusive transport of turbulent kinetic energy due to viscous diffusion <math> \nabla T_{\mathrm{visc, LES}} = 2\nu\frac{\partial \langle u_j's_{ij}\rangle}{\partial x_i} \cdot D/u_{\mathrm{b}}^3 </math>]] | ||
The pressure fluctuations (Fig. 15) play an important role in the diffusive TKE-transport. In some regions, the transport terms <math> \nabla T_{\mathrm{turb}}</math> and <math> \nabla T_{\mathrm{press}}</math> cancel each other while the horseshoe vortex oscillates in the horizontal direction according to the alternation of the back-flow and zero-flow mode. | The pressure fluctuations (Fig. 15) play an important role in the diffusive TKE-transport. It is the only positive term in the wall jet between <math> -0.6 < x/D < -0.5 </math> and therefore essential to understand the TKE balance in the wall jet. | ||
In some regions, the transport terms <math> \nabla T_{\mathrm{turb}}</math> and <math> \nabla T_{\mathrm{press}}</math> cancel each other while the horseshoe vortex oscillates in the horizontal direction according to the alternation of the back-flow and zero-flow mode. When the horseshoe vortex moves towards the cylinder to a region with a downward directed average flow (<math>\langle w \rangle <0 </math>), the vortex core with an instantaneous zero <math> w-</math>velocity induces a corresponding positive fluctuation <math> w'</math>. Therefore, the turbulent transport becomes altogether negative, and the transport due to pressure fluctuations become positve as <math> p'<0</math> in the vortex centre (low pressure), resulting in a mutual balance. | |||
The transport of TKE due to viscous diffusion shows an increased negative transport only close to the wall (see (Fig. 16), which is intuitive as viscous effects increase towards the wall in turbulent flows. In the remaining part, however, the amplitude of <math> \nabla T_{\mathrm{visc}}</math> is below <math> |0.05|u_{\mathrm{b}}^3/D</math>, and therefore, the contribution of this term to the TKE transport around the horseshoe vortex is of minor importance. | The transport of TKE due to viscous diffusion shows an increased negative transport only close to the wall (see (Fig. 16), which is intuitive as viscous effects increase towards the wall in turbulent flows. In the remaining part, however, the amplitude of <math> \nabla T_{\mathrm{visc}}</math> is below <math> |0.05|u_{\mathrm{b}}^3/D</math>, and therefore, the contribution of this term to the TKE transport around the horseshoe vortex is of minor importance. | ||
| Line 172: | Line 181: | ||
[[File:UFR3-35_LES_Epsilon.png|centre|frame|Fig. 17 b) Dissipation of turbulent kinetic energy <math> \epsilon_{\mathrm{LES, total}} = (2\nu\langle s_{ij}s_{ij}\rangle + 2\langle \nu_{\mathrm{t}} s_{ij}s_{ij}\rangle)\cdot D/u_{\mathrm{b}}^3 </math>, i.e. SGS-contribution included]] | [[File:UFR3-35_LES_Epsilon.png|centre|frame|Fig. 17 b) Dissipation of turbulent kinetic energy <math> \epsilon_{\mathrm{LES, total}} = (2\nu\langle s_{ij}s_{ij}\rangle + 2\langle \nu_{\mathrm{t}} s_{ij}s_{ij}\rangle)\cdot D/u_{\mathrm{b}}^3 </math>, i.e. SGS-contribution included]] | ||
The distribution of the dissipation shows a similar c-shaped structure as the TKE and the production term <math> P</math> due to the horizontal oscillations of the vortex. Three regions with a high dissipation rate can be located: (i) around the centre of the horseshoe vortex; (ii) underneath the horseshoe vortex inside the wall-parallel jet; and (iii) at the corner vortex V3. The amplitude of the measured dissipation rate exceeds the one stemming from the LES data due to measurement noise undermining the quality of the instantaneous fluctuating velocity gradients. The spatial resolution of the PIV was anyway too coarse to estimate the dissipation correctly such that we did not apply any correction to the experimental data. However, the experimental data serve as a qualitative comparison rather than a quantitative one as the spatial distribution in PIV is similar to the one in the LES. The dissipation rate and the production of the TKE do not cancel each other | The distribution of the dissipation shows a similar c-shaped structure as the TKE and the production term <math> P</math> due to the horizontal oscillations of the vortex. Three regions with a high dissipation rate can be located: (i) around the centre of the horseshoe vortex; (ii) underneath the horseshoe vortex inside the wall-parallel jet; and (iii) at the corner vortex V3. The amplitude of the measured dissipation rate exceeds the one stemming from the LES data due to measurement noise undermining the quality of the instantaneous fluctuating velocity gradients. The spatial resolution of the PIV was anyway too coarse to estimate the dissipation correctly such that we did not apply any correction to the experimental data. However, the experimental data serve as a qualitative comparison rather than a quantitative one as the spatial distribution in PIV is similar to the one in the LES. The dissipation rate and the production of the TKE do not cancel each other as the maximum amplitude in the centre of the horseshoe vortex is <math> \epsilon_{\mathrm{LES}}=0.066u_{\mathrm{b}}^3/D</math>, which is approximately one third of the production here. Furthermore, the maximum value of the production is located upstream of the horseshoe vortex indicating the role of the transport of small-scale structures between the location of <math> P_{\mathrm{max}}</math> towards <math> \epsilon_{\mathrm{max}}</math>. | ||
=== Mean convection of turbulent kinetic energy === | === Mean convection of turbulent kinetic energy === | ||
| Line 190: | Line 199: | ||
[[File:UFR3-35_LES_Budget.png|centre|frame|Fig. 19 b) Residual of turbulent kinetic energy budget <math> R_{\mathrm{LES}} = P + \nabla T - \epsilon_{\mathrm{total}} + C \cdot D/u_{\mathrm{b}}^3 </math>]] | [[File:UFR3-35_LES_Budget.png|centre|frame|Fig. 19 b) Residual of turbulent kinetic energy budget <math> R_{\mathrm{LES}} = P + \nabla T - \epsilon_{\mathrm{total}} + C \cdot D/u_{\mathrm{b}}^3 </math>]] | ||
The residual of the LES data is small in | The residual of the LES data is small in large regions <math> <|0.01|u_{\mathrm{b}}^3/D</math>. In particular, around the horseshoe vortex, the residual is close to zero. However, along the cylinder surface and the bottom wall the budget does not fully balance. On the one hand, we assign the large errors to the spatial resolution of the grid in the horizontal direction, which was obviously too coarse to fully resolve the developing boundary layer at the cylinder surface. On the other hand, the sensitivity with respect to the number of samples of the term <math> T_{\mathrm{turb}} = -\frac{1}{2}\langle u_i'u_j'u_j' \rangle </math> containing triple correlations of the velocity can be responsible | ||
the remaining error in the TKE budget. | the remaining error in the TKE budget. | ||
| Line 203: | Line 212: | ||
<math> c_{\mathrm{f}} = \frac{\langle \tau_{\mathrm{w}} \rangle}{\frac{\rho}{2} u_{\mathrm{b}}^2} </math>. | <math> c_{\mathrm{f}} = \frac{\langle \tau_{\mathrm{w}} \rangle}{\frac{\rho}{2} u_{\mathrm{b}}^2} </math>. | ||
The following plots were taken from the LES data only since the pressure is not contained in the PIV data and the spatial resolution in the experiment appeared to be too coarse to calculate the wall-shear stress | The following plots of pressure coefficient (Figs. 20 and 21) and friction coefficient (Fig.22) were taken from the LES data only since the pressure is not contained in the PIV data and the spatial resolution in the experiment appeared to be too coarse to calculate the wall-shear stress and hence the friction coefficient correctly. A more detailed discussion of this problem can be found in Schanderl et al. (2017). The first data point in the experimental data could be obtained at <math> z_1 \approx 0.0036D \approx 10 \mathrm{px}</math>. In the LES, the first grid point was at <math> z_1 \approx 0.0005D </math>, which is about a factor of 7 finer than the experimental results. | ||
A streamline plot in light grey is given for the sake of better orientation in a qualitative sense in | A streamline plot in light grey is given for the sake of better orientation in a qualitative sense in Figs. 21 and 22 showing the positions in the <math> z-</math>direction at which the profiles were extracted. The red symbols refer to the profiles near the wall indicated by the red solid line, whereas the blue symbols and the blue solid line refer to the profile at the height of the horseshoe vortex. | ||
[[File:UFR3-35_LES_Pressure.png|centre|frame|Fig. 20: Spatial distribution of the pressure coefficient <math> c_{\mathrm{p}}</math> ]] | [[File:UFR3-35_LES_Pressure.png|centre|frame|Fig. 20: Spatial distribution of the pressure coefficient <math> c_{\mathrm{p}}</math> ]] | ||
[[File:UFR3-35_cp.png|centre|frame|Fig. 21: Pressure coefficient <math> c_{\mathrm{p}}</math> ]] | |||
[[File:UFR3-35_cf.png|centre|frame|Fig. 22: Friction coefficient <math> c_{\mathrm{f}}</math>]] | |||
The accelerating wall-parallel jet is also perceptible in the distribution of the friction ceofficient <math> c_{\mathrm{f}} </math> (see Fig. 22), which was extracted at the first grid point. From the stagnation point S3 on, with zero wall-shear stress, the friction coefficient reveals a sharp peak underneath the | |||
The time-averaged pressure coefficient displayed in Fig. 20 increases in the horizontal direction when the flow approaches the cylinder. The horseshoe vortex is indicated by a local minimum. In the vertical direction towards the bottom wall of the flume, the pressure increases following the down-flow and has its local maximum at the stagnation point S3. At this point, the downflow is deflected in all directions forming an accelerating wall-parallel jet especially in the uptream direction. The acceleration is indicated by the decrease of the pressure coefficient along the local flow direction, which points in the upstream direction. At <math> x_{\mathrm{adj}}= -1.0 </math>, underneath the horseshoe vortex, the pressure coefficient shows a kink and decreases slower than before (see Fig. 21). | |||
The accelerating wall-parallel jet is also perceptible in the distribution of the friction ceofficient <math> c_{\mathrm{f}} </math> (see Fig. 22), which was extracted at the first grid point. From the stagnation point S3 on, with zero wall-shear stress, the friction coefficient reveals a sharp peak underneath the junction vortex V3. In the upstream direction, the wall-shear stress increases due to the accelerating jet until a plateau is reached. Here, the friction coefficient is almost constant at <math> |c_{\mathrm{f}}| = 0.01 </math>, which represents the maximum absolute value. It should be noted that the maximum is not located underneahth the horseshoe vortex. The distribution of <math> c_{\mathrm{f}} </math> is dominated by the wall-parallel jet rather than by the horseshoe vortex. Further upstream, the value of <math> c_{\mathrm{f}} </math> is small but negative, indicating the fading near-wall jet pointing still in the upstream direction. Unlike Apsilidis et al. (2015), we could not observe a second vortex here. | |||
= Datasets for download = | = Datasets for download = | ||
| Line 236: | Line 246: | ||
* Each column corresponds to the following data and is comma separated | * Each column corresponds to the following data and is comma separated | ||
|} | |} | ||
{| class="wikitable" style="text-align: center;" border="1" style="margin: auto;" | {| class="wikitable" style="text-align: center;" border="1" style="margin: auto;" | ||
| Column number | | Column number | ||
| 1 | | 1 | ||
| Line 250: | Line 264: | ||
| 9 | | 9 | ||
| 10 | | 10 | ||
| | |... | ||
|- | |- | ||
| '''PIV''' | | '''PIV''' | ||
| Line 271: | Line 277: | ||
| <math> \frac{\langle w'w'\rangle}{u_{\mathrm{b}}^2} </math> | | <math> \frac{\langle w'w'\rangle}{u_{\mathrm{b}}^2} </math> | ||
| <math> - </math> | | <math> - </math> | ||
| | |... | ||
|- | |- | ||
| '''LES''' | | '''LES''' | ||
| Line 292: | Line 290: | ||
| <math> \frac{\langle w'w'\rangle}{u_{\mathrm{b}}^2} </math> | | <math> \frac{\langle w'w'\rangle}{u_{\mathrm{b}}^2} </math> | ||
| <math> \frac{\langle u'v'\rangle}{u_{\mathrm{b}}^2} </math> | | <math> \frac{\langle u'v'\rangle}{u_{\mathrm{b}}^2} </math> | ||
|... | |||
|} | |||
{| class="wikitable" style="text-align: center;" border="1" style="margin: auto;" | |||
|+ style="caption-side:bottom;"|Tab. 6: Structure of the datasets | |||
| Column number | |||
|... | |||
| 11 | |||
| 12 | |||
| 13 | |||
| 14 | |||
| 15 | |||
| 16 | |||
| 17 | |||
| 18 | |||
| 19 | |||
|- | |||
| '''PIV''' | |||
|... | |||
| <math> \frac{\langle u'w'\rangle}{u_{\mathrm{b}}^2} </math> | |||
| <math> - </math> | |||
| <math> P\frac{D}{u_{\mathrm{b}}^3} </math> | |||
| <math> C\frac{D}{u_{\mathrm{b}}^3} </math> | |||
| <math> \nabla T_{\mathrm{turb}}\frac{D}{u_{\mathrm{b}}^3} </math> | |||
| <math> - </math> | |||
| <math> - </math> | |||
| <math> \epsilon\frac{D}{u_{\mathrm{b}}^3} </math> | |||
| <math> - </math> | |||
|- | |||
| '''LES''' | |||
|... | |||
| <math> \frac{\langle u'w'\rangle}{u_{\mathrm{b}}^2} </math> | | <math> \frac{\langle u'w'\rangle}{u_{\mathrm{b}}^2} </math> | ||
| <math> \frac{\langle v'w'\rangle}{u_{\mathrm{b}}^2} </math> | | <math> \frac{\langle v'w'\rangle}{u_{\mathrm{b}}^2} </math> | ||
| Line 302: | Line 333: | ||
| <math> c_{\mathrm{p}} </math> | | <math> c_{\mathrm{p}} </math> | ||
|} | |} | ||
Latest revision as of 15:55, 4 November 2020
Cylinder-wall junction flow
Evaluation
For the evaluation of the numerical and experimental data sets in the symmetry plane upstream of a wall-mounted cylinder the following quantities are presented:
- the streamlines
- the location of the characteristic flow structures
- selected vertical and horizontal profiles of the mean velocity components and as well as the Reynolds stresses and the turbulent kinetic energy
- the contour plots of the turbulent kinetic energy and its buget terms such as production, diffusive transport, dissipation, and mean convection
- horizontal profiles of the pressure coefficient , and the friction coefficient
Streamlines
The streamlines of the PIV and the LES data agree well according to Fig. 6. The plots are coloured by the normalized magnitude of the velocity in the symmetry plane, . The dashed and dash-dotted lines indicate the zero-isoline of the streamwise and vertical velocity component, respectively.
The approaching turbulent boundary layer is redirected downwards at the flow facing edge of the cylinder caused by a vertical pressure gradient. This downflow reaches the bottom plate of the flume at the stagnation point S3. Here, it is redirected (i) in the out-of-plane direction bending around the cylinder; (ii) towards the cylinder rolling up and forming the corner vortex V3; and (iii) in the upstream direction accelerating and forming a wall-parallel jet. The jet accelerates and exerts a large wall-shear stress on the bottom plate (see Fig. 22). Parts of the downflow form the horseshoe vortex V1. Upstream of this vortex system, the approaching flow is blocked and causes a saddle point S1 with zero velocity magnitude.
.
.
Location of the critical points
The position of the characteristic flow structures highlighted in the streamline plots is listed in the following table
| PIV | LES | |||
|---|---|---|---|---|
| S1 | ||||
| S2 | ||||
| S3 | ||||
| S4 | ||||
| V1 | ||||
| V3 |
Horizontal and vertical profiles of the velocity components and Reynolds stresses
The vertical profiles are extracted at the following positions with respect to the time-averaged position of the horseshoe vortex (see Fig. 7).
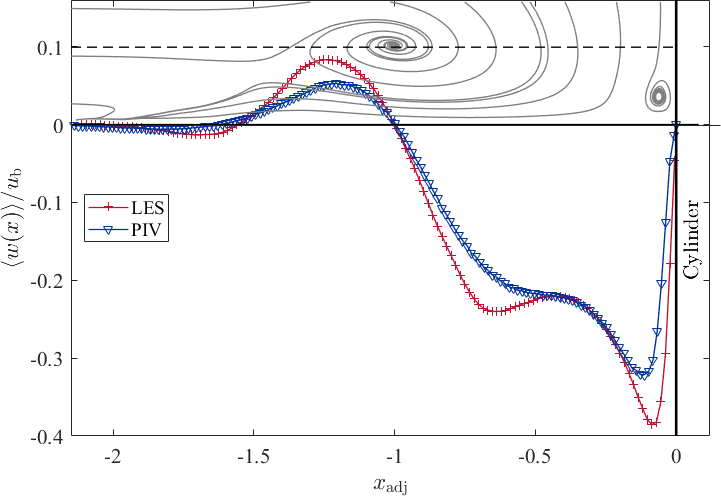
Since the positions of the horseshoe vortex in the LES and the PIV are slightly different, we use an adjusted coordinate, in order to compare the data at the same position in the flow. The coordinate is defined as follows (Schanderl 2018):
,
with , such that represents the time-averaged location of the horseshoe vortex centre .
The vertical profiles of the streamwise velocity are presented at the selected locations in Fig. 8. The wall-parallel jet starts to develop from S3 onward and the flow accelerates. At , a near-wall velocity peak appears, which becomes more pronounced in the upstream direction (see ). In this region, the wall-shear stress reaches on the one hand its maximum value and on the other hand reveals a plateau-like shape (this is shown and discussed later, see Fig. 22). This means that the largest values of the gradient appear. Underneath the horseshoe vortex, the reverse flow decelerates and the near-wall-peak of the velocity lifts from the bottom plate and becomes less distinct. Further upstream, the near-wall peak of the streamwise velocity disappears as the wall-parallel jet fades out.
Due to the evaluation of the PIV images by an interrogation-window-based cross correlation, the strong gradient at the wall cannot be fully resolved, and therefore, the near-wall peak of the streamwise velocity is damped in the experimental data.
The vertical profiles of the Reynolds normal stress , the Reynolds shear stress and the resulting turbulent kinetic energy comprising only streamwise and vertical fluctuating velocity components (inplane with respect to the symmetry plane) are presented in Fig. 9a) to c), respectively. Note, that the range of the axis is not constant for the sake of better visibility. The experimental and numerical data agree reasonably well both with regard to amplitude and shape. Again, the quality of the PIV data near the wall is undermined by the strong gradients being evaluated using interrogation windows.
The largest values of are found underneath the horseshoe vortex. This is the foot of the c-shaped distribution of the turbulent kinetic energy. In the wall jet at and the Reynolds stresses are generally small which is explained by the fact that the wall jet is strongly accelerated in upstream direction which leads to a negative production term in the turbulent kinetic energy balance (see next section). Large Reynolds shear stress can be found between the horseshoe vortex and the stagnation point S1 at . Large values of the turbulent kinetic energy can be found around the horseshoe vortex center (due to large ) and under the horseshoe vortex near the wall (due to ).
There is a specific issue interesting for modeling. In the lower region of the wall jet (between the velocity maximum of the wall jet and the wall) the Reynolds shear stress does not change sign as does the vertical velocity gradient and hence does not follow the eddy viscosity hypothesis. This is due to the complex flow and turbulence behaviour in this region. Consequently, eddy-viscosity models would have difficulties to reproduce the near-wall shear-stress distribution.
Analysing the profile of the vertical velocity component along the axis at the height of the horseshoe vortex (see Fig. 10), reveals on the one hand the clockwise rotation of the vortex, and on the other hand two minima between the horseshoe vortex and the cylinder. At , the peak in the downwards directed flow stems from the downflow along the cylinder front face, while the second local minimum at approximately represents the downwards rotation of the horseshoe vortex. Both data sets agree well in shape. However, the LES data indicate higher amplitudes in general, as the stagnation point at the cylinder front at which the approach flow is deflected and the downflow evolves, is located at the water level in the LES. On the other hand it was shifted downwards in our experiment, due to the plate of acrylic glass placed at the water surface. This is, however, not an artefact as a bow wave (surface roller) would evolve in this area if this plate were not present according to e.g. Melville 2008. Therefore, the downwards deflected part of the flow is smaller in the experiment and hence the HV system becomes smaller too.
Distributions of the Reynolds stresses and the inplane turbulent kinetic energy at the height of the horseshoe vortex are shown in Fig. 11 and reveal similar distributions for the PIV and LES results. At the centre of the vortex, the normal stresses, and consequently the turbulent kinetic energy as well, reveal a peak, which wears off in the up- and downstream direction. In addition, the downflow close to the cylinder surface generates stresses as well. The shear stress plays a minor role in the region between the cylinder and the horseshoe vortex, while it becomes negative upstream of the horseshoe vortex indicating the interference of the approaching flow with the horseshoe vortex.
Distribution of turbulent kinetic energy and its budgets terms: production, diffusive transport, dissipation and convection
Turbulent kinetic energy
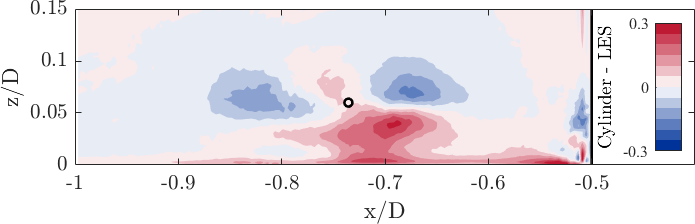
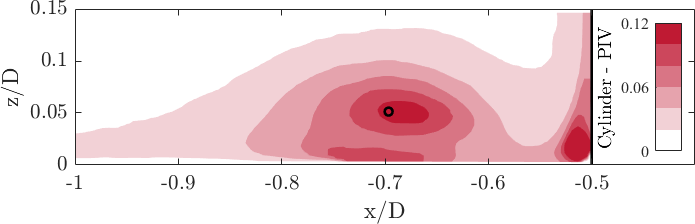
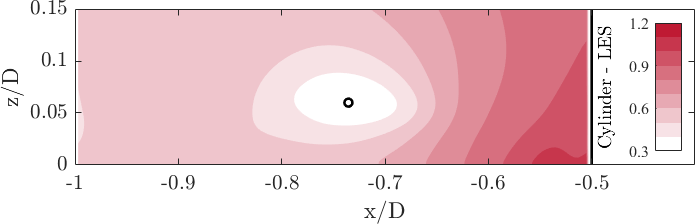
The spatial distribution of the time-averaged in-plane turbulent kinetic energy reveals on the one hand the well-known c-shaped structure (e.g. Paik 2007) with the largest amplitude at the centre of the horseshoe vortex stemming from vertical fluctuations induced by the horizontal oscillations of the horseshoe vortex (see Fig. 12 a) and b). The lower branch of the c-shape contains mainly streamwise (horizontal) fluctuations linked to the dynamics of the wall-parallel jet. On the other hand, the experimental and numerical data sets show high similarity and agree well with each other, as the peak amplitude is approximately the same: ; . The black circle marks the centre of the horseshoe vortex.
When the fluctutuations of the three-dimensional velocity vector are used to determine the turbulent kinetic energy , the additional out-of-plane component does not change the shape of the distribution (see Fig. 12 c). However, the amplitudes at the horseshoe vortex centre and inside the lower branch of the c-shape both increase due to the vortex bending around the cylinder entailing increased out-of-plane fluctuations, e.g. at V1: .
The budget equation of the turbulent kinetic energy reads:
,
and is the balancing sum of the production , the diffusive transport term , the dissipation , and the mean convection . In case of the LES data, these terms were calculated using the entire three dimensional velocity vector and the corresponding fluctuations. However, the influcence of the out-of-plane component is small due to symmetry (Schanderl et al. 2017). The individual terms are determined as follows:
- production:
- diffusive transport:
- dissipation: , and as the fluctuating rate-of-strain tensor
- in the LES, the dissipation consists of a resolved and a subgrid scale (SGS) part:
- mean convection: (steady state)
The individual terms of the budget equation of the TKE are normalized by and presented in the following subsections.
Production of turbulent kinetic energy
Fig. 13 a) and b) show the TKE production using the PIV and LES results, respecively. The main region of positive production of turbulent kinetic energy can be found upstream of the centre of the hoseshoe vortex (black circle) and inside the wall-parallel jet. The amplitude of both data sets is about in the region of the horseshoe vortex, while the LES data resolve the TKE production in the jet in more detail than the PIV data. The amplitudes here are and . The oscillations of the horseshoe vortex are responsible for causing fluctuations, which in turn produce turbulent kinetic energy.
From the stagnation point S3 onwards in the upstream direction, the TKE production is negative, meaning that inside the accelerating jet TKE is transferred to mean kinetic energy. When the jet decelerates at about , the jet becomes more unstable, fluctuations occur, and therefore, becomes positive.
Diffusive transport of turbulent kinetic energy
The diffusive transport of TKE is presented in Fig. 14 and can be split up into three individual terms: the transport due to turbulent fluctuations, due to pressure fluctuations, and due to viscous diffusion. Since the pressure in general is not contained in the PIV data, the velocity-pressure correlations, which are required to obtain the transport due to pressure, cannot be calculated, as well. Therefore, we present the three terms individually if available.
The distribution of the turbulent transport shows a similar structure as the one of the production. In the region of large positive TKE production, we observe a large negative transport. In particular close to the wall at , the large production of is nearly balanced by the turbulent transport .
Positive transport indicates that TKE is transported towards these regions. They can be found above the centre of the horseshoe vortex. Accroding to Apsilidis et al. (2015), vertical eruptions from the wall occur here, which coincides with our observations.
The pressure fluctuations (Fig. 15) play an important role in the diffusive TKE-transport. It is the only positive term in the wall jet between and therefore essential to understand the TKE balance in the wall jet. In some regions, the transport terms and cancel each other while the horseshoe vortex oscillates in the horizontal direction according to the alternation of the back-flow and zero-flow mode. When the horseshoe vortex moves towards the cylinder to a region with a downward directed average flow (), the vortex core with an instantaneous zero velocity induces a corresponding positive fluctuation . Therefore, the turbulent transport becomes altogether negative, and the transport due to pressure fluctuations become positve as in the vortex centre (low pressure), resulting in a mutual balance.
The transport of TKE due to viscous diffusion shows an increased negative transport only close to the wall (see (Fig. 16), which is intuitive as viscous effects increase towards the wall in turbulent flows. In the remaining part, however, the amplitude of is below , and therefore, the contribution of this term to the TKE transport around the horseshoe vortex is of minor importance.
Dissipation of turbulent kinetic energy
The dissipation is the sink term in the budget of the TKE transport equation, as the TKE was produced and transported by and , respectively, and is dissipated into heat by . The dissipation is positive by definition, and therefore, it appears with a negative sign in the budget equation. In the LES data, the modelled dissipation due to subgird stresses is included and was quantified to be approximately one third of the total dissipation rate. Fig. 17 shows the dissipation rate calculated from PIV and LES data.
The distribution of the dissipation shows a similar c-shaped structure as the TKE and the production term due to the horizontal oscillations of the vortex. Three regions with a high dissipation rate can be located: (i) around the centre of the horseshoe vortex; (ii) underneath the horseshoe vortex inside the wall-parallel jet; and (iii) at the corner vortex V3. The amplitude of the measured dissipation rate exceeds the one stemming from the LES data due to measurement noise undermining the quality of the instantaneous fluctuating velocity gradients. The spatial resolution of the PIV was anyway too coarse to estimate the dissipation correctly such that we did not apply any correction to the experimental data. However, the experimental data serve as a qualitative comparison rather than a quantitative one as the spatial distribution in PIV is similar to the one in the LES. The dissipation rate and the production of the TKE do not cancel each other as the maximum amplitude in the centre of the horseshoe vortex is , which is approximately one third of the production here. Furthermore, the maximum value of the production is located upstream of the horseshoe vortex indicating the role of the transport of small-scale structures between the location of towards .
Mean convection of turbulent kinetic energy
The approaching flow separates from the bottom wall of the flume, and consequently, becomes unstable with increasing fluctuations. Therefore, the TKE increases along the streamlines, which is indicated by the negative mean convection upstream of the horseshoe vortex (see Fig. 18). The same applies for the wall-parallel jet. After the deflection at S3, the jet accelerates, which decreases TKE in the first place. When the jet starts to decelerate () the flow becomes more unstable and the TKE increases. Underneath the horsehsoe vortex, changes sign again and the TKE decreases further upstream.
Budget of turbulent kinetic energy
Finally, the sum of the above mentioned terms is presented in Fig. 19 as the total budget of the TKE. Since the PIV data cannot provide information concerning the pressure, the corresponding residual will not cancel out. In addition, the amplitude of the dissipation rate is uncertain in the experimental data.
Nevertheless, when analysing the distribution and amplitude of the residual of the TKE budget obtained from PIV, we observe a similar structure to the one of . Therefore, the missing piece in the experimental data of this flow configuration is the contribution of the pressure fluctuations to the transport mechanisms of the TKE (Jenssen 2019).
The residual of the LES data is small in large regions . In particular, around the horseshoe vortex, the residual is close to zero. However, along the cylinder surface and the bottom wall the budget does not fully balance. On the one hand, we assign the large errors to the spatial resolution of the grid in the horizontal direction, which was obviously too coarse to fully resolve the developing boundary layer at the cylinder surface. On the other hand, the sensitivity with respect to the number of samples of the term containing triple correlations of the velocity can be responsible the remaining error in the TKE budget.
Pressure coefficient , and of the friction coefficient
The pressure coefficient is computed as:
,
while the friction coefficient is determined as:
.
The following plots of pressure coefficient (Figs. 20 and 21) and friction coefficient (Fig.22) were taken from the LES data only since the pressure is not contained in the PIV data and the spatial resolution in the experiment appeared to be too coarse to calculate the wall-shear stress and hence the friction coefficient correctly. A more detailed discussion of this problem can be found in Schanderl et al. (2017). The first data point in the experimental data could be obtained at . In the LES, the first grid point was at , which is about a factor of 7 finer than the experimental results.
A streamline plot in light grey is given for the sake of better orientation in a qualitative sense in Figs. 21 and 22 showing the positions in the direction at which the profiles were extracted. The red symbols refer to the profiles near the wall indicated by the red solid line, whereas the blue symbols and the blue solid line refer to the profile at the height of the horseshoe vortex.
The time-averaged pressure coefficient displayed in Fig. 20 increases in the horizontal direction when the flow approaches the cylinder. The horseshoe vortex is indicated by a local minimum. In the vertical direction towards the bottom wall of the flume, the pressure increases following the down-flow and has its local maximum at the stagnation point S3. At this point, the downflow is deflected in all directions forming an accelerating wall-parallel jet especially in the uptream direction. The acceleration is indicated by the decrease of the pressure coefficient along the local flow direction, which points in the upstream direction. At , underneath the horseshoe vortex, the pressure coefficient shows a kink and decreases slower than before (see Fig. 21).
The accelerating wall-parallel jet is also perceptible in the distribution of the friction ceofficient (see Fig. 22), which was extracted at the first grid point. From the stagnation point S3 on, with zero wall-shear stress, the friction coefficient reveals a sharp peak underneath the junction vortex V3. In the upstream direction, the wall-shear stress increases due to the accelerating jet until a plateau is reached. Here, the friction coefficient is almost constant at , which represents the maximum absolute value. It should be noted that the maximum is not located underneahth the horseshoe vortex. The distribution of is dominated by the wall-parallel jet rather than by the horseshoe vortex. Further upstream, the value of is small but negative, indicating the fading near-wall jet pointing still in the upstream direction. Unlike Apsilidis et al. (2015), we could not observe a second vortex here.
Datasets for download
- PIV data: Media:UFR3-35_X_data.txt
- LES data: Media:UFR3-35_C_data.zip
- LES: friction coefficient Media:UFR3-35_C_cf.txt
- How to read in the data as an example (MatLab): Media:UFR3_35_read_data.m
The datasets are structured as follows:
- 2D plots of the PIV have data points
- 2D plots of the LES have data points
- The .txt files are reshaped such as each column has entries
- The first 11 lines of the .txt files belong to the header, which are indicated by the #-symbol
- Each column corresponds to the following data and is comma separated
| Column number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
| PIV | ... | ||||||||||
| LES | ... |
| Column number | ... | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| PIV | ... | |||||||||
| LES | ... |
Contributed by: Ulrich Jenssen, Wolfgang Schanderl, Michael Manhart — Technical University Munich
© copyright ERCOFTAC 2019