AC 6-08 Best Practice Advice
High speed centrifugal compressor
Application Challenge 6-08 © copyright ERCOFTAC 2004
Best Practice Advice
Best Practice Advice for the AC
Key Fluid Physics
The physics of a high speed compressor are governed by the pressure gradients linked to the curvature of the blade channel (blade-to-blade; axial-to-radial) and the effects of centrifugal and Coriolis forces. This leads, together with the influence of the end-wall regions, to a highly non-uniform flow especially in the rear part of the blade channel (jet/wake). Losses are caused by
• skin friction (with the comparatively great passage lengths)
• mixing (secondary flow; tip clearance flow)
• shocks (at the leading edge of the splitter blades)
An important additional physical effect that occurs in high speed compressors is the strong coupling between the thermodynamics and the aerodynamics. An incorrect estimate of the loss production (entropy change) by CFD leads to an error in the density via the thermodynamic equation of state for an ideal gas:
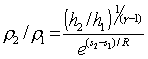
For a specified mass flow the error in the density causes an error in the volume flow and this in turn leads to an incorrect velocity field, for example the error in meridional velocity is inversely proportional to the error in density:
The incorrect estimate of the velocity field leads to errors in velocity triangles, which in turn can also have an additional effect on the density. For example an underprediction of losses leads to an increase in density. This reduces the meridional velocity and causes a higher work input and enthalpy change across the impeller, which in turn also leads to an increase in density. For this reason high speed turbomachinery predictions are very much more sensitive to errors in the CFD than their incompressible low-speed counterparts.
The resulting flow field can be judged by the following DOAPs:
• impeller efficiency
• pressure ratio across the impeller
• Mach number distribution along the flow path
• angle of the relative velocity at the impeller exit
• extent of zones of separated flow and location of shocks
(although a clearly defined parameter for the quantification of these is not available)
The flow is at high Reynolds number and high turbulence levels, so that apart from a short laminar section at the leading edge, the flow is turbulent throughout the flow passage. It is compressible and the compression is assumed to be adiabatic, i.e., with no heat flux into or from the surrounding walls. The working fluid is dry air.
Application Uncertainties
The following uncertainties have been found due to a lack of knowledge or to restrictions in the measurements:
• The exact tip clearance width at operating condition is unknown. A larger tip clearance width results in higher losses (due to higher tip clearance flow) and a reduction in pressure rise because of the reduced effective blade surface and the increased leakage losses. For the present case an increase of the tip clearance width by 50% led to a reduction in total pressure rise by 6-8% and a reduction in isentropic efficiency by up to 2%. This level of uncertainty in the running clearance level of high-speed centrifugal compressors is typical of most applications, as the clearance level is determined by a wide range of effects (mechanical deformation of impeller due to centrifugal stresses, thermodynamic expansion of the impeller and the casing caused by the temperature gradients, mechanical deformation of the casing caused by the high pressure level, and possible shifts of the rotor in the axial direction as a result of clearances in the bearings.)
• No information was given about the flow quantities at the inlet (i.e. profiles for total pressure, flow direction, turbulence) for the different operating points. For the solely given profile the total pressure was constant (apart from the end-wall regions) and the flow direction nearly axial. Constant total pressure and axial flow direction have therefore been assumed for all operating points.
• The L2F method is only capable of measuring the velocity component perpendicular to the laser beam. Therefore the measured velocity is always equal or smaller than the actual velocity. As the laser beam was positioned perpendicular to the casing, the error increases towards the hub.
• The measured pressure ratio and efficiency of the rotor has to be interpreted with care, as the total pressure at the rotor outlet was not directly measured but derived from the total temperature, mass flow and the static pressure (at shroud) assuming a certain blocking factor taken from an initial CFD simulation. Wrong values for the blocking factor and/or the averaged static pressure can influence the results.
Computational Domain and Boundary Conditions
The computational domain should cover the region well up- and downstream of the stage. For the current case, the domain was chosen to start at 60% of the inlet shroud diameter before the spinner and to end at 120% of the diffuser outlet diameter. To avoid recirculation with inflow into the domain on the outlet plane, the outlet should be slightly pinched.
For simplicity reasons, the blade hub fillets can be neglected, but one has to keep in mind, that by doing this the massflow corresponding to a given pressure rise is slightly increased as the blockage of the fillets is absent.
The flow direction at the inlet is assumed to be purely axial in the absolute frame of reference (this assumption was confirmed by the only given inlet profile). If the gradient ∂Π/∂mred is high the combination of total pressure at inlet and average static pressure at outlet should be used. When the gradient ∂Π/∂mred becomes too small the outlet boundary condition should be changed to a massflow boundary condition.
UFR4-05 states that the flow regime is influenced by the inlet boundary layer thickness. For this AC it was assumed that an inlet region of 0.6·D1 is enough to develop a realistic profile at the inlet of the impeller. This should be checked for future simulations.
To minimize the numerical error only the rotor should be simulated in the rotating frame of reference. The inlet region and the diffuser are to be connected to the rotor by a frozen rotor interface and solved in the stationary frame of reference. Only one passage is modeled.
Discretisation and Grid Resolution
Although a purely 2nd order discretization scheme is desirable, it was found, that the main flow features (DOAPs) were already well captured with a slightly less accurate discretization scheme (i.e. 2nd order Linear Profile Skew Upstream Differencing Scheme with a blending of 5% Upwind Differencing Scheme).
It was found that a maximum residual greater than 5.0E-05 still influences the DOAPs (especially the isentropic efficiency). For high quality results a maximum residual of not more than 5E-05, better 1E-05, should therefore be aspired to.
While the grid is fine enough to capture most of the main flow features it is still too coarse to resolve the shock giving a smeared shock-front. For a better accuracy the region around the leading edge should be refined.
No explicit study has been done for the influence of grid refinement and near wall distance (y+). The chosen values are based on experience and a compromise between accuracy and performance of the simulation. However, less than 30 grid points in the spanwise direction should not be used, as “the number of cells in the spanwise direction is of great importance”, according to UFR4-05. Furthermore, as the tip clearance flow is one of the key features, the clearance should be resolved with 5-6 grid points at minimum in combination with the scalable wall function to account for the resulting small y+ values.
Physical Modelling
The impact of different turbulence models has been studied in the UFR 4-05 “Curved duct/pipe flow (accelerating)”, UFR3-03 “2D Boundary layers with pressure gradients” and UFR3-08 “3D boundary layers under various pressure gradients, including severe adverse pressure gradient causing separation”.
Although UFR4-05 is an accelerating flow and therefore the effect of turbulence model reduced, it still found a tendency for better prediction with the two equation transport model compared to the algebraic / mixing length models. For boundary layers under adverse pressure gradients, UFR3-03 recommends the use of the SST model, the Spalart-Allmaras model or the ω-equation based Reynolds Stress models for the 2D case, while UFR3-08 advises the use of a cubic version of the non linear k-ε model or a Reynolds stress model for the 3D case with separated flow. This difference in recommendation may be due to the fact that the two UFR´s did not both test all of the available models.
Following UFR4-05, the use of the superior two equation transport models is even more advisable for the decelerating flow in a centrifugal impeller. All simulations of this AC have been performed using the standard k-ε model with scalable wall functions, which is in agreement with the most relevant UFRs, when looking at the main flow features. However, if a simulation of higher accuracy is intended, the k-ω SST model or a Reynolds stress model should be used, as e.g. the linear k-ε model under-estimates the extension of the separated regions.
Recommendations for Future Work
• The independency of the solution of further grid refinement should be checked.
• Following the recommendations of UFR3-03 and UFR3-08 the simulations should be performed using the k-ω SST model or a Reynolds stress model. For this, the near-wall distance of the first grid point has to be reduced to be in the order of unity, and will lead to grids that are probably too fine for normal engineering design applications.
• The influence of the inlet conditions such as turbulence parameters and boundary layers should be studied.
© copyright ERCOFTAC 2004
Contributors: Beat Ribi; Frank Sieverding - MAN Turbomaschinen AG Schweiz; Sulzer Innotec AG