UFR 4-18 Test Case

Flow and heat transfer in a pin-fin array

Front Page

Description

Test Case Studies

Evaluation

Best Practice Advice

References

Test Case Study

Brief Description of the Study Test Case

General Description

The experiments from Ames et al. (2004, 2005, 2006, 2007) described later in this section deal with the flow of air around 8 staggered rows of 7.5 heated pins (see figure ??), spaced at P=2.5D in both stream-wise and span-wise directions (based on center to center distances). The diameter of the pins is set to 0.0254 m (1 inch) and the channel height is twice the diameter (H=2D).

The Reynolds number $Re_{D}$ is based on the pin diameter and the average gap bulk velocity. Three Reynolds numbers have been tested : $Re_{D}=3,000$, $Re_{D}=10,000$ and $Re_{D}=30,000$. This latter is computed only with URANS and the first one only with LES.

The bottom wall is heated with a constant heat-flux whereas the other walls are adiabatic (Ames et al.). All the flow properties can be taken constant, the Prantl number is equal to 0.71.

Figure ??: 2D Sketch of Ames et al. experiment

Test Case Experiments

General Description of the experiment

The description given in the present section has been given by F. Ames during the $15^{th}$ Ercoftac SIG15 Workshop. More information could also be found in Ames et al. (2004, 2005, 2006, 2007). The objective of the experiments was to create a database that includes heat transfer distributions on the pin fins and endwall, pressure distributions on the pin fins and endwall, documentation of turbulence intensities and scales, and measurements of turbulence and velocity distributions across the channels. The research was conducted in a small bench top wind tunnel (see Figure ??) which included a small blower capable of producing a flow of $0.3m^{3}/s$ at a static pressure rise of 2000 Pa. The pin fin array was designed in an 8 row, 7 1/2 pin per row staggered arrangement. Both the cross passage (S/D) and stream-wise (X/D) pin spacing were equal to 2.5 while the pin height to diameter (H/D) was 2. The pin diameter was chosen to be equal to 2.54 cm. The flow conditioning system first spreads out the flow from the blower to the width of the array using a two-stage multi-vane diffuser. A heat exchanger was installed in the system downstream from the diffuser to control the tunnel temperature in order to impose a constant value. The heat exchanger discharges the flow into a screen box consisting of three nylon window screens to reduce the cross stream velocity variations in the flow. Directly downstream of the screens, the flow enters a smooth 2.5 to 1 area ratio nozzle prior to entering the test section. The pin fin array test section begins 7.75 D upstream of the centerline of the first row of pins and ended 7.75 D downstream of the centerline of the last row of pins. The inlet total temperature and pressure and static pressures were measured 5 D upstream from the row 1 centerline and the exit static pressures were measured 5 D downstream from row 8. Downstream from the test section the flow was directed through a 90° rectangular elbow then a rectangular channel followed by a second 90° elbow before entering a 20.8 cm diameter orifice tube used to measure the array flow rate. Tests were conducted at three Reynolds numbers : 3 000, 10 000, and 30 000. The Reynolds number is based on the maximum velocity (also called the gap velocity $V_{G}$. The gap bulk velocity is determined between two adjacent pins of the same row. Taking $V_{0}$ and $V_{BG}$ as the inlet and gap velocities, respectively, and considering mass conservation, one obtains $V_{BG}=P/(P-D)V_{0}$. Fluid properties were determined from the inlet conditions.

A 2D sketch of the original experimental configuration is given in Figure ??. In the experiment, the distance between the inlet (beginning of the test section; end of a converging nozzle) and the center of the first cylinders is equal to 7.75D. The distance between the center of the last cylinders and the test section is also equal to 7.75D.

The remaining description will focus on the test-case which is studied here and on the data which are used in the present work, the heat transfer on the pins, the pressure distributions on the endwalls, availabe spectra ... are not included.

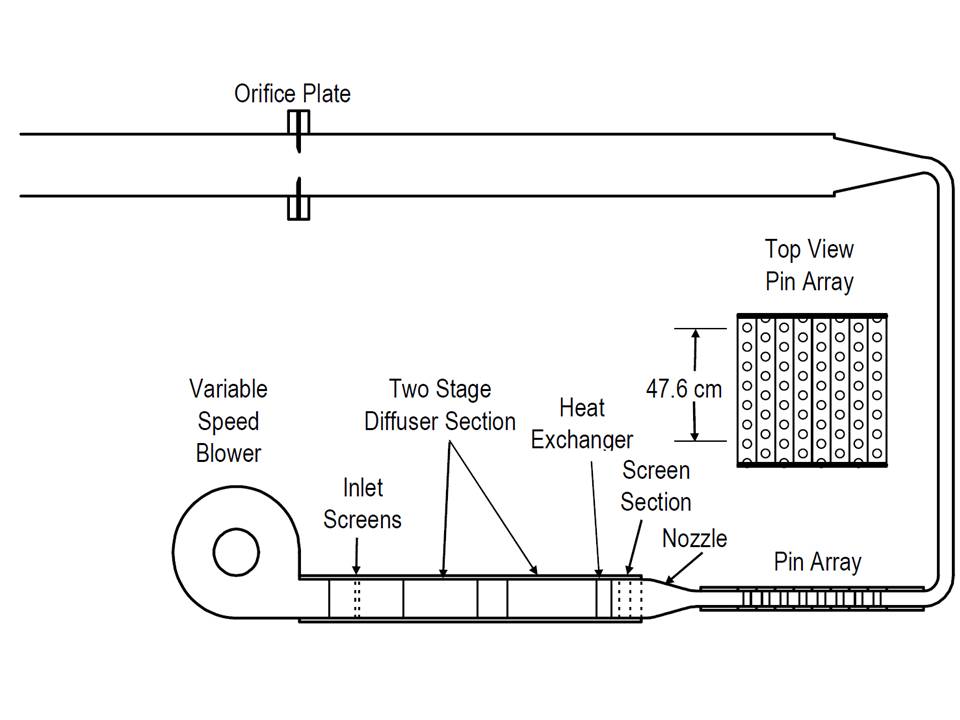
Figure ??: Sketch of Ames et al. experimental rig (image taken from Ames et al. (2007))

Pressure loss coefficients

The inlet static pressure is monitored by five static taps positioned across one pin spacing 5 diameters upstream from the centerline of row 1. The exit static pressure taps are similarly located but 5 dia downstream of row 8. Both the inlet and exit have probe access ports that allow determination of inlet and exit total pressure The test section exhausts into a duct, which eventually is directed into an orifice tube. The sharp-edged orifice tube is used to determine the array mass flow rate. This allows measuring the pressure drop coefficient.

The file containing the experimental data might be uploaded from File:Headloss.xls.

Pin fin surface static pressure

The pins were fabricated from clear acrylic. The midspan surface static pressure distributions were acquired using a 2.54 cm diameter pin which contained 20 equally spaced 0.76 mm static pressure taps around the midspan perimeter. Measurements were made in 6° increments by indexing the pin. An example of pressure distribution is given in figure ??. The file containing the experimental data might be uploaded from File:Cp midline.zip.

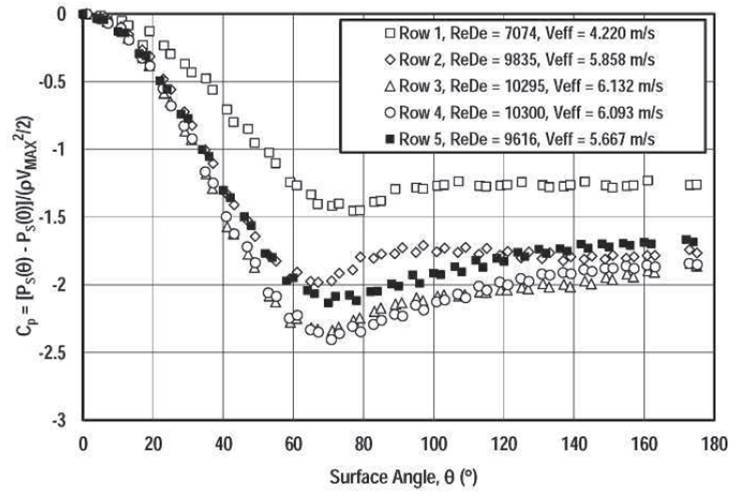
Figure ?? : Midline pressure coefficient distribution, row 1-5, $Re_{D}=100000$ (image taken from Ames et al. (2005))

Pin fin array turbulence and velocity measurements

Array turbulence and velocity measurements were acquired using single and X wire hotwire probes powered by a TSI IFA 300 constant temperature anemometry unit. A special low velocity jet was developed to calibrate the wires from 0.4 m/s through 40 m/s to enable measurements of turbulence and velocity distributions over a 10 to 1 range in Reynolds number. An example of profile obtained along the line B1 for row 5 is given in figure ??

The file containing the experimental data might be uploaded from File:Dynamics.zip.

Figure ?? : Mean and r.m.s. stream-wise velocity component along line B for different Reynolds numbers - row 5 (image taken from Ames et al. (2006))

Endwall heat transfer measurements

Full surface endwall heat transfer measurements were acquired using a constant heat flux test surface and a FLIR SC500 IR camera. A constant surface heat flux boundary condition was generated using three, 15.28 cm wide by 68.58 cm long, 0.023 mm thick Inconel foils with 0.127 mm thick Kapton backing and 0.05 mm thick acrylic adhesive. The three foils were adhered to a 0.89 mm thick sheet of fiberglass epoxy board which in turn was epoxied to a 3.81 cm thick section of isocyanurate foam. The three foils were connected in series. The current through the foil and the voltage across the center foil was used to determine the surface heat flux. The surface heat flux was corrected for both local radiation and conduction loss. The radiation loss assumed the emissivity of the surface was 0.96 and the conduction loss was based on a simple 1-D model. The camera was equipped with a special lens which allowed a much wider angle (45°) and a much closer focal plane (6.35 cm) than the tandard lens. This allowed the camera to acquire a 130 by 260 pixel image (3.175 cm by 6.35 cm) through a 5.08 cm diameter zinc selenide window. At each measurement location, the camera location was indexed on the pins to ensure a consistent camera location for all the measurements. The accuracy of the surface temperature measurement was enhanced by the calibration of the camera on a calibration surface through the same zinc selenide window, the manual resetting of the camera every three or four pictures, and the averaging of 9 images for each heat transfer realization. The driving force temperature difference was calculated as heated endwall surface temperature corrected for the inlet temperature during the test and for the local calibration less the unheated endwall surface temperature corrected for the inlet temperature and the local calibration. The temperature difference also accounted for the bulk temperature rise of the air due to endwall heating.

The normalized Nusselt number obtained in the experiments between X/D=-2.5 and X/D=20 is shown in figure figure ??.

The experimental data giving these distributions might be downloaded from File:Thermal Fields bottom wall.zip. This files allows plotting the normalized Nusselt number (by its average as defined earlier) along the lines $Y=0$ and $Y=1.25D$ as shown on figure ?? (one can use other lines for comparison).

The average of the Nusselt number on the bottom wall between X/D=-2.5 and X/D=20 is given in File:Nusselt average.xls.

Figure ?? : The normalized Nusselt number for different Reynolds numbers (image taken from Ames et al. (2007), form top to bottom: $Re_{D}=3000$, $Re_{D}=10000$, $Re_{D}=10000$.

Figure ?? : The lines along which the normalized Nusselt number are plotted

Data uncertainties

Uncertainties in the reported values were estimated based on the root sum square method described by Moffat (1988). The uncertainty in the reported Reynolds number was determined to be +/- 3% due to the possible error in the flow rate measurement. The largest uncertainty for the midspan pressure coefficient was estimated to be +/- 0.075 due to the very low dynamic pressure at the low Reynolds number condition (Re = 3 000). However, the uncertainty in the pressure coefficient was no more than +/- 0.025 at the higher two Reynolds numbers. Uncertainty in the measurement of velocity using a hot wire was estimated to be +/- 3% except in the near wall region where positional and conduction effects could substantially increase the possible error. Additionally, at high turbulence levels single wire velocities can be significantly overestimated if traverse fluctuation velocities, normal to the wire become high. For example at 30% intensity levels velocities can be overestimated by 4%. The reported value of turbulence intensity had an uncertainty of approximately +/- 3%. The reported uncertainties in Nusselt number are estimated to be as high at +/- 12%, +/-11.4%, and +/-10.5% for the 3 000, 10 000, and 30 000 Reynolds numbers respectively in the endwall regions adjacent to the pins and +/- 9% away from the pin. Note that the combination of several methods reduced the uncertainty band of the surface temperature measurement from about +/-2 °C to about +/- 0.7 °C. Uncertainty estimates were determined using a 95% confidence interval.

Experimental results used for the CFD evaluation

All 1-D profiles are drawn along lines A1, B & C (see Figure ??). The main lines for the velocity components and the Reynolds stresses are A1 and B and the main one for the pressure coefficient is C (mid-span location).

The exact positions of the lines are the folowing :

• A1- Line at mid-span location (Y/D=5/4 from center of the pin or Y/D=3/4 from surface of the pin) between two adjacent pins of the same row along the channel height (Z-axis).
• B - Surface to surface line between two adjacent pins of the same row at mid height (Z/D=1.0) along the span (Y-axis).
• C - Circumferential line around the pin surface from 0°-180°, at mid height of the pin (Z/D=1.0). Angle measurements are taken to be zero (0°) on the leading edge of the pins with a counter-clockwise orientation.

Data will be shown for sevral rows, mainly X/D=0 (row 1), X/D=2.5 (row 2), X/D=5.0 (row 3), and X/D=10.5 (row 5). Note that profiles along line A1 will be shown only for $Re_{D}=30000$.

The velocity components and the Reynolds stresses will be normalized by the average gap bulk velocity $V_{BG}$. If $V_{0}$ stand for the bulk velocity at the inlet, one has thank to mass conservation: $V_{BG}=P/(P-D)V_{0}$.

As the wall heat flux $q_{w}$ is imposed, the Nussel number is given by $Nu=q_{w}D/(\lambda (T_{w}-T_{ref}))$ where $T_{w}$ and $T_{ref}$ are respectively the time average temperature at the wall and a reference temperature and $\lambda$ is the thermal conductivity. $T_{ref}$ takes into account the increase in the bulk temperature of the fluid from the heated surface as it flows down the array (see the Nusselt number calculated in Nordquist (2006)).

Then, at a given $X$, one has: $T_{ref}=q_{w}S_{h}(X)/(\rho C_{p}V_{0}S_{i})$.

Where $S_{h}(X)$ is the heated surface from $-10D$ to $X$. Nordquist (2006) uses an estimation of this surface using $S_{h}=(10D+X)S_{htot}/L_{X}$ where $S_{htot}$ is the total heated surface (here the surface from $-10D$ to $X=32.5D$) and $L_{X}$ the total length of the domain ($L_{X}=42.5D$). $\rho$, $C_{p}$ and $S_{i}$ are the fluid density, the specific heat and the surface inlet, respectively. As one has the relation $V_{0}S_{i}=2V_{0}HP=2V_{BG}(P-D)H$, the reference temperature function of $X$ reduces to :

$T_{ref}=((10D+X)q_{w}S_{htot}/(2\rho C_{p}V_{BG}(P-D)HL_{x})$

The following data will be analysed for the different computations

• The pressure loss coefficient $f=\Delta P/(2\rho {V^{2}}_{BG}N_{rows})$ where $\Delta P$ is the pressure drop between the planes X/D=-5 and X/D=22.5 (see figure ??) and $N_{rows}$ the number of rows ($N_{rows}=8$ in the present case).
• Pressure Coefficient along line C for rows 1, 2, 3 and 5. $C_{p}=2(p-p_{max})/\rho {V^{2}}_{BG}$ where $p_{max}$ is the maximum pressure (the pressure at the stagnation point).
• The mean stream-wise velocity profiles ($U/V_{BG}$), its r.m.s value $u'/V_{BG}$ along lines A1 and B.
• $Nu_{av}$, the average of the Nusselt number on the bottom wall between X/D=-2.5 and X/D=20.
• The normalised Nusselt number on the bottom wall ( $Nu/Nu_{av}$)

Figure ?? : Rows numbering and lines (A1, B and C) locations

CFD Methods

The computational domain

The computational domain consists of 8 by 2 pins (see figure??). All solid surfaces (pins, bottom and the top walls) are set to no-slip solid walls. The inlet of the channel is set at a distance $L_{U}=10D$ upstream from the center of the first row of pins, whereas the outlet is $L_{D}=15D$ downstream from the center of the last row of pins. Note that these two distances are both equal to 7.75D in the experimental setup but are not enough to perform CFD calculations (see Afgan et al. (2007) and Parnaudeau et al. (2008)), in particular for the upstream channel, unless one respresents the nozzle of the experiment (see figure) what will lead to a much more expensive compurations.

Figure ??: The computational domain

General Description of the computations

All the computations have been carried out with Code_Saturne (see Archambeau et al. (2004)), EDF in-house open source CFD tool for incompressible flows (go to http://code-saturne.org for more details and download). It is based on an unstructured collocated finite-volume approach for cells of any shape (one uses here only hexa conforming meshes). It uses a predictor/corrector method with Rhie and Chow interpolation and a SIMPLE-like algorithm for pressure correction. An implicit reconstruction method is used for the gradients while dealing with the non-orthogonalities.

Four Models, LES using the dynamic model (Germano et al. (1991), Lilly (1992)) kω-SST (Menter (1994)), φ-model (Laurence et al. (2005)), and EB-RSM (Manceau and Hanjalic (2002)) are used to simulate the present test-case (the main computations and results have been presented in Benhamadouche et al. (2012)). All the models are all wall-resolved and use no-slip boundary conditions for the velocity vector and appropriate boundary conditions for the turbulent quantities (see the corresponding articles). Inlet conditions for the velocity and turbulent quantities will be specified separately for LES and URANS computations. No sensistivity tests to the boundary conditions are reported.

The temperature is treated as a passive scalar with an imposed temperature at the inlet, an imposed heat flux at the bottom wall and adiabatic conditions elsewhere. The effect of the thermal boundary condition on the bottom wall is studied in LES by taking a fixed temperature instead of a fixed heat flux.

From a practical point, one takes the density, the inlet velocity, the specific heat coefficient and the diameter of the pins equal to unity and the viscosity equal to $1/Re_{D}$. The Prandtl number is equal to 0.71 and thus the fluid conductivity $\lambda =1/(PrRe_{D})$. As the temperature is passive, one takes the inlet temperature equal to 0 and the imposed heat flux equal to unity.

Free Outlet boundary conditions are used for all the variables at the outlet and an implicit periodic condition is used in the lateral direction for all the variables.

In order to mimic the experiment with physical values, here are typical ones which might be used for the simulations (the pressure is equal to the atmospheric pressure and the computation is incompressible):

$Re_{D}$	$T_{inlet}$ (°K)	$V_{0}$ (m/s)	$\nu$ (m²/s)	$\rho$ (kg/m^3)	$C_{p}$ (J/kg/K)	$\lambda$ (W/m/K)	$q$ (W/m²)
3000	300	1.06	0.000015	1.2	1005	0.0255	100
10000	300	3.54	0.000015	1.2	1005	0.0255	300
30000	300	10.62	0.000015	1.2	1005	0.0255	1000

Large Eddy Simulation Computations

General Features

Large Eddy Simulation (see Benhamadouche (2006) for its implementation in Code_Saturne) uses a dynamic Smagorinsky model (Germano et al. (1991), Lilly (1992)) in which the Smagorinsky constant cannot be negative and is bounded by its value validated in a channel flow ($C_{S}=0.065$). This model has been successfully used recently by Afgan et al. (2011) for the flow around a single and side-by-side cylinders. A fully centered convection scheme is applied for the velocity components and the temperature. For this latter, a slope test which switches to a first order upwind scheme is utilized to limit the overshoots. The time advancing scheme is second order based on Crank-Nicolson/Adams Bashforth scheme (the diffusion including the velocity gradient is totally implicit, the convection is semi-implicit and the diffusion including the transpose of the velocity gradient is explicit). A turbulent Prandtl number equal to 0.5 is used while solving the temperature with LES.

At the inlet, a uniform velocity is imposed without any synthetic or precursor turbulence generation.

Very fine LES simulations have been carried out for the Reynolds numbers $Re_{D}=3,000$ and $Re_{D}=10,000$.

Wall treatment in LES

A particular attention has been paid to the grid refinement at the wall. Two meshes containing 18 million and 76 million cells have been used to simulated the two Reynolds numbers $Re_{D}=3,000$ and $Re_{D}=10,000$, respectively. Figures ??, ?? and ?? show instantenous snapshots of the non-dimensional wall normal distance. The two meshes are of the same quality for this quantity (the maximum value is higher for $Re_{D}=10,000$ but this is rather a local effect). This quantity is not the only one of interest; one has to refine in the stream-wise and span-wise directions. Figure ?? gives the mean value of the non-dimensional distances in the three directions. It can be seen that the refinement is the one needed for a wall resolved LES everywhere except around the centerlines of the pins and downstream of the last row. However, the refinement in these regions is still very satisfactory.

Figure ??: Instantaneous snapshots of the non-dimensional wall normal distance to the wall, LES at $Re_{D}=3,000$ with 18 million computational cells

Figure ??: Instantaneous snapshots of the non-dimensional wall normal distance to the wall, LES at $Re_{D}=10,000$ with 76 million computational cells

Figure ??: Mean non-dimensional distances at the near-wall computational cell, LES at $Re_{D}=10,000$ with 76 million computational cells - top left: non-dimensional distance in the stream-wise direction - top right: non-dimensional distance in the span-wise direction - bottom: non-dimensional distance in the wall normal direction

Sensitivity to the sub-grid scale model

Sensitivity studies have been carried out to quantify the effect of the subgrid scale model and showed that its effect is not that importance at the present level of refinement. Figures  ?? and ?? show profiles of the r.m.s. values of the stream-wise velocity component and of the normalized Nusselt numbers, respectively. The effect seems almost negligible.

The following table gives the pressure loss coefficient and the averaged Nusselt number for the simulations with and without the sub-grid scale model. One can see that there is an effect on heat transfer which has not been seen locally.

Figure ??: R.m.s. of the stream-wise velocity component along line B - effect of the sub-grid scale model on LES at $Re_{D}=3000$

Figure ??: Local Nusselt number on the bottom wall - effect of the sub-grid scale model on LES at $Re_{D}=3000$

	With a sub-grid scale model (dynamic)	Without a sub-grid scale model
Pressure Loss coefficient (f)	0.1076	0.1089
Error on f	3	2
Averaged Nusselt Number ($Nus_{av}$)	21.6	20.8
Error on $Nus_{av}$	2	6

One can see than the effect on the pressure loss coefficient is almost negligible which is not the case on the heat transfer.

URANS computations

General Features

By default, a centered scheme with a slope test is used for the velocity components and the temperature and a 1st order upwind scheme for the turbulent quantities. The time advancing scheme is in this case a first order Euler one.

The φ-model uses the elliptic relaxation introduced by Durbin (1991). In both utilized first moment closures, a Simple Gradient Diffusion Hypothesis (SGDH) is naturally utilized for the temperature equation with a turbulent Prantl number equal to 0.9. The EB-RSM is presented in \cite{Manceau2002} and uses the concept of elliptic blending for the scrambling and the dissipation terms of the Reynolds stresses. The temperature is solved with a Generalized Gradient Diffusion Hypothesis (GGDH) approach using a constant equals to 0.23.

The use of more advanced models such us the AFM (Algebraic Flux Model), the EB-GGDH (extension of the elliptic blending concept but for the scrambling and dissipation terms of the turbulent heat fluxes (see Dehoux et al. (2012) for more details)) or the EB-AFM didn't change the results that much, at least for global quantities such as the mean Nusselt number.

While using URANS, a uniform velocity and 5% turbulence intensity are imposed. This latter condition allows to provide the production terms with the Reynolds stresses mandatory to their development. The inlet conditions for URANS computations are thus given by:

The turbulent kinetic energy $k$ is given by:

$k={\frac {3}{2}}V_{BG}^{2}I_{k}^{2}$

where $V_{BG}$ is the average gap bulk velocity and $I_{k}$ the turbulent intensity.

In the case of the Reynolds stress model, the Reynolds stresses are given by:
$R_{ij}={\frac {2}{3}}k\delta _{ij}$

The turbulent dissipation $\varepsilon$ is given by:
$\varepsilon ={\frac {C_{\mu }^{3/4}k^{3/2}}{0.1\kappa D_{H}}}$

where $\kappa =0,42$, $C_{\mu }=0.09$ and $D_{H}=2H$ stands for the hydraulic diameter of the inlet.

In the case on the kω-SST, one takes $\omega ={\frac {\varepsilon }{C_{\mu }k}}$.

URANS simulations have been carried out for the two higher Reynolds numbers; $Re_{D}=10,000$ and $Re_{D}=30,000$

As shown below for the EB-RSM, a systematic sensitivity study to the mesh refinement and to the numerical options has been carried out in order to have a high confidence on the computations.

Grid convergence study

The grid convergence study has been performed for the three URANS models and for the two Reynolds numbers. As first-moment and second moment closures exhibit totally different behaviors, the sensitivity study is carried out for all the models. One gives hereafter the study performed for $Re_{D}=10,000$ and the EB-RSM model. Three levels of refinement are used for all the models. The coarse mesh is successively refined by a factor 2 in all the directions. The finest mesh has approximately 17M cells for $Re_{D}=10,000$ (it contains approximately 29M cells for $Re_{D}=30,000$).

Figures ??, ?? and ?? show the pressure coefficient along the pin midline and the mean and r.m.s. values of the stream-wise velocity component along line B. As the computations are unsteady, note that the r.m.s. values, or more generally the Reynols stresses are the sum of the resulved part and the modelled one: $R_{ij}=R_{ij}^{res}+R_{ij}^{mod}$. The resolved and modeled part are shown separately in figure ??. One can observe that the results of the two finer meshes do not match, the coarse mesh results being very far from the actual ones. Thus, all the results given in "Evaluation" for a turbulence model will be those obtained with the finest mesh (called here "very fine mesh". The ideal would have been to add a fourth level of refinement but this would have expensive in terms of CPU time. Note also that the refinements could have been "more intelligent" than refining by a factor of 2 in all the directions. However, the sensitivity study to the numerical options (see next section) make us confident is the fact that the results obtained with the finest mesh are very close to the converged ones.

Figure ??: Mean pressure coefficient along the pin midline, EB-RSM at $Re_{D}=10,000$ - grid convergence study

Figure ??: Mean stream-wise velocity component along line B, EB-RSM at $Re_{D}=10,000$ - grid convergence study

Figure ??: R.m.s. of the stream-wise velocity component along line B, EB-RSM at $Re_{D}=10,000$ - grid convergence study

Figure ??: Modelled r.m.s. of the stream-wise velocity component along line B, EB-RSM at $Re_{D}=10,000$ - grid convergence study

Figure ??: Resolved r.m.s. of the stream-wise velocity component along line B, EB-RSM at $Re_{D}=10,000$ - grid convergence study

Sensivity study to the convection scheme

By default, a centered scheme with a slope test is used for the velocity components and the temperature and a 1st order upwind scheme for the turbulent quantities. The scheme called centered in figures ?? and ?? consists in a fully centered scheme for the velocity components and a centered scheme for all the other scalar quantities (Reynolds stresses, dissipation rate, temperature). As it can be observed, the effect is everywhere negligible on the mean and r.m.s. quantities except around row 2 where it is noticeable but limited. This conclusion is important as a pure centered scheme on the velocity components doesn't seem to change the unsteadiness. Moreover, using a centered scheme for the turbulent quantities doesn't affect the results. Other tests have been carried out by introducing for example outer iteration for pressure/velocity coupling and none of them exhibited a noticeable effect.

Figure ??: Mean stream-wise velocity component along line B, EB-RSM at $Re_{D}=10,000$ - sensitivity study to the numerical scheme on the very fine mesh

Figure ??: r.m.s. of the stream-wise velocity component along line B, EB-RSM at $Re_{D}=10,000$ - sensitivity study to the numerical scheme on the very fine mesh

The main computations

The folowing table summerizes the main computations which will be exhibited in "Evaluation". Note that "niba = number of iterations before averaging" and "nifa = number of iterations for averaging".

Main computations

Test-case	$Re_{D}$	$V_{BG}$ (m/s)	$V_{B}$ (m/s)	Turbulence Model	Time step (s)	niba	nifa	mean $CFL_{max}$
LES3000	3000	2.02	1.21	Dynamic Smagorinsky	0.0015	325000	217000	0.8
LES10000	10000	6.18	3.71	Dynamic Smagorinsky	0.0002	130000	245000	0.8
EBRSM10000	10000	6.18	3.71	EB-RSM	0.001	160000	140000	1.8
PHI10000	10000	6.18	3.71	φ-model	0.001	50000	250000 (*)	1
kwSST10000	10000	6.18	3.71	kω-SST	0.001	80000	220000 (*)	1.3
EBRSM30000	30000	18.53	11.12	EB-RSM	0.0000625	64000	308000	0.6
PHI30000	30000	18.53	11.12	φ-model	0.00025	40000	125000	0.9
kwSST30000	30000	18.53	11.12	kω-SST	0.00025	50000	150000	1.8

(*) 100000 would have been enough to converge in time

Possible sources of uncertainty

The main possible sources of uncertainty are:

• The inlet boundary conditions, in particular for URANS as one has to prescribe turbulence in URANS computations.
• The periodicity assumption in the spanwise direction.
• The uniformity of the heat flux which is probably not the case in the experiment.

---

Contributed by: Sofiane Benhamadouche — EDF

Front Page

Description

Test Case Studies

Evaluation

Best Practice Advice

References

© copyright ERCOFTAC 2024