CFD Simulations AC2-08: Difference between revisions
| Line 89: | Line 89: | ||
====<span class="titlemark"> Computational Domain, Spatial Discretization and Boundary Conditions==== | ====<span class="titlemark"> Computational Domain, Spatial Discretization and Boundary Conditions==== | ||
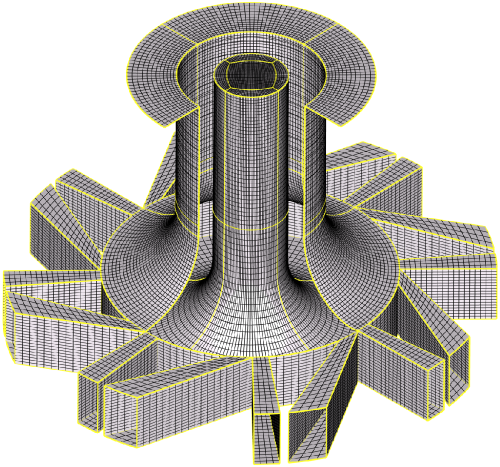
As illustrated in Fig. | As illustrated in Fig. 4.1 and 4.2 the computational domain starts after the plenum chamber at the inlets of the tangential and radial channels. Here the mass flow given by the measurements has been set. No additional velocity fluctuation is forced here since the inclusion of the geometry upstream of the nozzle exit has been found to be sufficient to allow the turbulent structures to form. The equivalence ratio has been set to <span class="math">ϕ </span><nowiki>= 0</nowiki><span class="math">.</span>83 at the inlet since the methane-air mixture has been verified by the measurements to be mixed homogeneously. The diameter of the computational domain matches the extend of the coflowing air issuing with 0<span class="math">.</span>5m/s. The boundaries in radial and axial direction have been found to be sufficiently far away from the region of interest (i.e. the swirler exit region). The block structured grid contains 3.2 million control volumes and has been elliptically smoothed to obtain a better orthogonality. The grid has been refined towards the near nozzle region whereas it gets coarser with increasing distance to spare cells. | ||
[[Image:swirler_mesh_scale.png|left|frame|Figure 4.1: Computational domain of the swirl nozzle. The blockstructure is indicated by the yellow block boundaries.]] | |||
< | <br style='clear:both' /> | ||
[[Image: | [[Image:comput_domain_only_scale.png|left|frame|Figure 2.3: Dimensions of the computational domain with a cut-out of the elliptically smoothed mesh. Boundary conditions are indicated by arrows.]] | ||
<br style='clear:both' /> | |||
</ | |||
====<span class="titlemark"> Physical Modeling==== | ====<span class="titlemark"> Physical Modeling==== | ||
Revision as of 12:51, 11 January 2011
Premixed Methane-Air Swirl Burner (TECFLAM)
Application Challenge 2-08 © copyright ERCOFTAC 2011
Introduction
The Tecflam configuration has been investigated by means of RANS (Reynolds Averaged Navier Stokes) and LES (Large Eddy Simulation). An overview will be presented in this section. Some details of the most recent work done by [#Xkuenne_les_2011 Kuenne et al.] ([#Xkuenne_les_2011 2011]) will be given. In order to avoid an overload of information the interested reader is referred to the cited references for a detailed discussion.
Overview of Simulations
Since measurements of temperature and species mass fractions exist only for the 30 kW configuration only this case has been investigated by means of numerical simulations. The studies are summarized in table [#x1-16001r2 2].
|
|
|
|
|
|
|
|
| Isothermal (30iso), CFD-Code / Publication | Reacting (PSF-30), CFD-Code / Publication | |
|
|
|
|
| RANS |
FASTEST / [#Xhahn_investigation_2008 Hahn et al.] ([#Xhahn_investigation_2008 2008]) |
Ansys CFX / [#Xkuenne_hybrid_2009 Kuenne et al.] ([#Xkuenne_hybrid_2009 2009]) |
|
|
|
|
| LES |
FASTEST / [#Xhahn_investigation_2008 Hahn et al.] ([#Xhahn_investigation_2008 2008]) |
FASTEST / [#Xkuenne_les_2011 Kuenne et al.] ([#Xkuenne_les_2011 2011]) |
|
FASTEST / [#Xkuenne_les_2011 Kuenne et al.] ([#Xkuenne_les_2011 2011]) |
||
|
|
|
|
CFD Code
The three-dimensional finite volume code FASTEST uses block-structured, hexahedral, boundary fitted grids to represent complex geometries. Regarding the velocity, spatial discretization is based on multi-dimensional Taylor series expansion [#Xlehnhaeuser_improved_2002 Lehnhaeuser and Schaefer] ([#Xlehnhaeuser_improved_2002 2002]) to ensure second order accuracy on arbitrary grids. To assure boundedness of scalar quantities the TVD-limiter suggested by [#Xzhou_transonic_1995 Zhou et al.] ([#Xzhou_transonic_1995 1995]) is used. An explicit Runge-Kutta scheme is used for the time advancement of momentum and species mass fractions with temperature dependent transport coefficients. The code solves the incompressible, variable density, Navier-Stokes equations where an equation for the pressure correction is solved within each Runge-Kutta stage to satisfy continuity. The solver is based on an ILU matrix decomposition and uses the strongly implicit procedure [#Xstone_iterative_1968 Stone] ([#Xstone_iterative_1968 1968]) to take advantage of the block-structure.
Computational Domain, Spatial Discretization and Boundary Conditions
As illustrated in Fig. 4.1 and 4.2 the computational domain starts after the plenum chamber at the inlets of the tangential and radial channels. Here the mass flow given by the measurements has been set. No additional velocity fluctuation is forced here since the inclusion of the geometry upstream of the nozzle exit has been found to be sufficient to allow the turbulent structures to form. The equivalence ratio has been set to ϕ = 0.83 at the inlet since the methane-air mixture has been verified by the measurements to be mixed homogeneously. The diameter of the computational domain matches the extend of the coflowing air issuing with 0.5m/s. The boundaries in radial and axial direction have been found to be sufficiently far away from the region of interest (i.e. the swirler exit region). The block structured grid contains 3.2 million control volumes and has been elliptically smoothed to obtain a better orthogonality. The grid has been refined towards the near nozzle region whereas it gets coarser with increasing distance to spare cells.
Physical Modeling
The turbulent flowfield is approximated by means of LES (Large Eddy Simulation). Sub grid fluxes of momentum are accounted for by the eddy viscosity approach proposed by [#Xsmagorinsky_general_1963 Smagorinsky] ([#Xsmagorinsky_general_1963 1963]) where the model coefficient is obtained by the dynamic procedure of [#Xgermano_dynamic_1991 Germano et al.] ([#Xgermano_dynamic_1991 1991]) with a modification by [#Xlilly_proposed_1992 Lilly] ([#Xlilly_proposed_1992 1992]). Outside of the reaction zone a gradient approach has been chosen for the sub grid flux of scalar quantities with a turbulent Schmidt number of 0.7.
The method to treat the chemical reaction is based on a thickened flame approach ([#Xbutler_numerical_1977 Butler and O’Rourke] ([#Xbutler_numerical_1977 1977]); [#Xorourke_two_1979 O’Rourke and Bracco] ([#Xorourke_two_1979 1979]); [#Xangelberger_large_1998 Angelberger et al.] ([#Xangelberger_large_1998 1998]); [#Xcolin_thickened_2000 Colin et al.] ([#Xcolin_thickened_2000 2000]); [#Xcharlette_power-law_2002 Charlette et al.] ([#Xcharlette_power-law_2002 2002])) coupled to FGM (flamelet generated manifolds, [#Xvan_oijen_modelling_2000 van Oijen and de Goey] ([#Xvan_oijen_modelling_2000 2000]); [#Xvan_oijen_modeling_2001 van Oijen et al.] ([#Xvan_oijen_modeling_2001 2001])) tabulated chemistry using the mixture fraction and a reaction progress variable. Details about the method and its verification can be found in [#Xkuenne_les_2011 Kuenne et al.] ([#Xkuenne_les_2011 2011]).
Contributors: Johannes Janicka (EKT), Guido Kuenne (EKT), Andreas Dreizler (RSM)