UFR 1-01 Description: Difference between revisions
| Line 82: | Line 82: | ||
The following works have been chosen as being the most appropriate, currently available, information on which comparisons have been made between CFD and experiment, and they represent a very good match for what is required for this UFR : | The following works have been chosen as being the most appropriate, currently available, information on which comparisons have been made between CFD and experiment, and they represent a very good match for what is required for this UFR : | ||
* | * Cumber et al. (1994) present a comparison between CFD and experiment for the case of a ''moderately'' under-expanded jet, applying two turbulence models: a standard, and a modified, version of the ''k-ε'' scheme. | ||
* | * A second paper, Cumber et al. (1995) presents further comparison between CFD and experiment, using the same turbulence models as previously, but this time considering their application to the ''highly'' under-expanded jet. Details of the turbulence models, discretisation schemes, boundary conditions, and computational mesh are given. | ||
* | * Very recently, Bartosiewicz et al. (2002) present results using a second-moment closure methodology, for the cases of both the ''moderately'' and ''highly'' underexpanded jet. Their results are, usefully, based on the same experimental work as studied by Cumber (above), and they also cross-plot their results with a modeling study of the same problem by Pao and Abdol-Hamid (1996), who used similar modeling to that of Cumber. | ||
The above CFD work is compared with several experimental studies, for both the near-field (in the under-expanded region) and in the far-field. However, the focus of this UFR lies purely in the near field, since far-field behaviour is considered elsewhere in other UFR documentation. This still leaves us, however, with two good quality experimental studies with which both Cumber’s, and Bartosiewicz’s CFD work has been compared, covering the near-field behaviour of both moderately- and highly- under-expanded jets. Although neither of these experiments, apparently, were performed with CFD validation in mind, this should not affect their suitability for use here : | The above CFD work is compared with several experimental studies, for both the near-field (in the under-expanded region) and in the far-field. However, the focus of this UFR lies purely in the near field, since far-field behaviour is considered elsewhere in other UFR documentation. This still leaves us, however, with two good quality experimental studies with which both Cumber’s, and Bartosiewicz’s CFD work has been compared, covering the near-field behaviour of both moderately- and highly- under-expanded jets. Although neither of these experiments, apparently, were performed with CFD validation in mind, this should not affect their suitability for use here : | ||
Revision as of 11:32, 11 March 2010
Underexpanded jet
Underlying Flow Regime 1-01 © copyright ERCOFTAC 2004
Description
Preface
The complex nature of turbulent fluid flow, in realistic applications, is usually a combination of many different underlying flow processes. One aspect of QNET-CFD is to identify all these important component flows, and subject these, individually, to scrutiny. The lessons learnt to date on modelling such flows, including meshing, turbulence modelling, and boundary conditions, will then be documented.
A CFD practitioner, having identified the underlying flow processes that shape their own real application, will be able to refer to (the appropriate combination of) these documents and gain understanding on the current knowledge of modelling the underlying physical effects, and hence, be in a good position to apply a high quality CFD methodology from the outset.
This document focusses on the particular underlying flow regime (UFR) of the turbulent, under-expanded, jet formed from releases of a gas from high-pressure sources, and considers only its initial expansion, by means of a complex shock structure. The subsequent effects, including jet impingement, or the jets far-field dispersion, are considered elsewhere in QNET-UFR documentation.
Introduction
The under-expanded, axisymmetric, free jet is perhaps one of the simplest flows which comprises both shock-wave containing compressiblity effects and turbulent mixing. It is a flow seen in many practical applications, including jets from propulsion systems (especially in aerospace applications), and releases (deliberate or accidental) from high pressure pipeline/storage facilities.
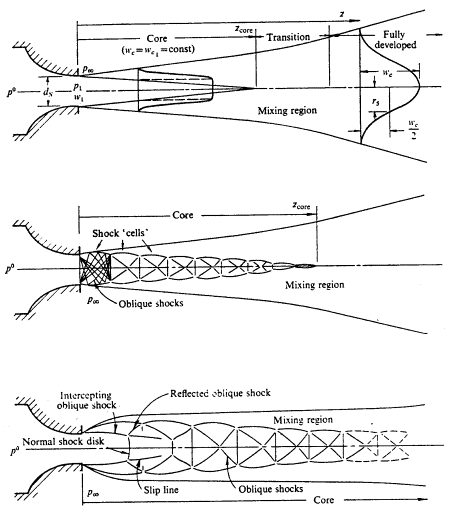
The profile of the jet, during its initial expansion phase, is primarily dependant on the pressure ratio between the reservoir stagnation conditions (P0) and the ambient pressure, (P∞). This is neatly described by Donaldson and Snedeker (1971), from where Figure 1 has been taken. A jet may be categorised into one of three types :
i.) A subsonic jet, when 1.0 < P0/P∞ < 1.89 , as illustrated in the upper plot in Figure 1. Here the pressure everywhere in the jet, including at its throat pressure, P1, will be equal to the ambient pressure, P∞. The jet is characterised by a potential core, surrounded by a mixing region. The radius of this potential core decreases to zero with increasing downstream distance, with the core not existing beyond zcore downstream. Beyond this point, the jet goes through a transitional phase as it continues to expand (as the velocity decays, in order to conserve axial momentum), and will eventually reached a fully developed, self-similar, state.
Figure 1 : Three variations in jet flow from a sonic nozzle,taken from Donaldson & Snedeker (1971), reproduced with permission from Cambridge University Press.
ii.) A moderately under-expanded jet, when 2.08 < P0/P∞ < 3.85, as illustrated in the middle plot in Figure 1. If the pressure of the jet is higher than the critical (sonic) pressure, shocks begin to be formed at the nozzle exit, and the nozzle pressure, P1, will be higher than ambient; in the range 1.1 < P1/P∞< 2.0. The jet expands to ambient pressure though a series of oblique shock waves (or shock diamonds). The boundaries of what was the potential core in the above (subsonic) case are now characterised by the outer boundary of the shock cells, outside of which, the pressure is in equilibrium with ambient and mixing can take place. Downstream, beyond the range of this core, the jet becomes entirely subsonic, and can be assumed to expand as would a free jet.
iii.) A highly under-expanded jet, when P0/P∞ > 3.85, is characterised by the presence of a Mach disk, and is illustrated in the lower sketch in Figure 1. The increased pressure in the reservoir results in the structure of the first shock cell changing. The rapid expansion along the jets centerline produces a very low axial pressure, and the recompression towards the end of the first cell exceeds the limiting case for the oblique shocks. A normal shock wave is therefore formed, (a Mach disk) a short distance downstream of the nozzle. Upstream of the Mach disk, the flow is supersonic, downstream it is subsonic. The nozzle pressure will now be higher, P1/P∞ > 2.0. This profile will remain if the pressure is increased further, and may result in additional axial shock disks, as the subsonic flow downstream of the first shock is rapidly accelerated, and a second axial shock disk may be evident when P1/P∞> 4.0
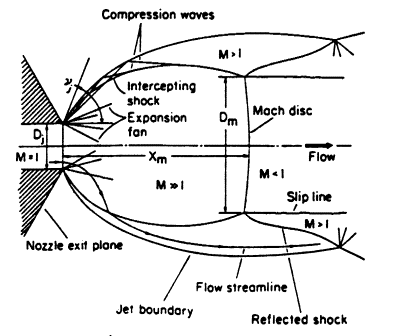
More detail of the shock structure in this initial cell was described by Crist et al. (1966), from where Figure 2 has been taken. An expansion fan forms at the nozzle exit, out towards the free pressure-boundary of the jet, and these are reflected as weak pressure waves, which join to form the intercepting shock wave. The flow in the jet core is clearly supersonic, as is the flow outside this intercepting shock, although of a lower Mach number. Just downstream of the Mach disk, the flow will be subsonic on the jet axis, though the flow outside of the intercepting shock remains supersonic. A triple point is formed where the Mach disk, intercepting shock, and reflected shock meet. Both the distance to this Mach disk, and its radius, can be expected to increase with increasing Mach number.
In this document, it is the latter two cases that will be studied — namely the cases of the moderately- and highly- under-expanded jets.
Figure 2 : Schematic diagram of first shock cell of a highly under-expanded jet. Originally published in Crist et al. (1966), Copyright © 1966 by the American Institute of Aeronautics and Astronautics, Inc. Reprinted with Permission.
Review of UFR studies and choice of test case
At first glance, one would presume that the under-expanded jet would be a relatively simple test case, and one which would have undergone exhaustive study, both experimentally and computationally. However, surprisingly, this is not the case (certainly since here we are interested purely in the under-expanded jet itself, not in the effects of its dispersion or impingement).
Studies of the under-expanded jet are by no means new, and the structure of the jet has been known for some time, eg Pack (1948) and Adamson & Nicholls, (1959). One of the major problems facing experimentalists, however, has been ways of taking measurements, unobtrusively, within the under-expanded regime. Observations of the shock structure, enabling measurements to be made of the Mach disk diameter and location, can be made optically — for example the Schlieren photography used by Crist at al (1966).
Pressure-probe measurements were made by Donaldson and Snedeker (1971), however, they noted problems with this methodology because of a low frequency instability within the jet. More recently, measurements have been made using LDA and laser-induced-fluorescence (eg Cheuch et al, 1989), offering data on both the mean and fluctuating components of velocity and concentration. However, Cheuch did have problems with seeding for the LDA in the shock containing regions because of the rapidly changing velocity.
2.1 Review of nearly-relevant work
Before describing the experimental and CFD work on which this UFR documentation will be based, it is perhaps worth highlighting some of the other studies, which encompass an under-expanded jet, yet which, for various reasons, have not been adopted here:
Birch et al. (1984) performed measurements on the concentration field in a sonic jet of natural gas, for the cases of both moderately- and highly- under-expanded jets. Their interest was in ways of describing an effective source such that these jets could be regarded as a classical free jet, and a photograph showing the familiar shock-diamond structure is presented. In a later paper, (Birch et al., 1987), a similar jet, though of air rather than natural gas, is studied using hot-film anemometry to gain data on the velocity field. Unfortunately, however, both of these papers from Birch and co-authors consider only the far-field behaviour of the jet, downstream of the shock-wave expansion region, and as a result, do not help us here in the study of the under-expanded regime.
There have been many studies of the impinging sonic and supersonic jets. To name but a few, Leschziner and Ince (1995), interested in the operation of VSTOL aircraft, looked at both inviscid and transonic jets, impinging on the ground (and the effect that a pair of jets from the two engines have on each other). This work is unusual in that it applies a higher-order second moment closure, and demonstrates the superiority of these schemes over the simple k-ε eddy viscosity model. Cumber et al. (1997) modelled an impinging moderately under-expanded jet, using the k-ε eddy viscosity model, but with modifications, as from Sarkar et al. (1991) — this modification will be discussed later. Experimental studies have also considered the effects on the shock structure of oblique jet impingement (for example Ignatius and Rathakrishnan, 1996). None of these works, however, give us information for the simple under-expanded jet.
Indeed, another study worth mentioning, which may be of interest to the reader, is that of Leschziner, Batten and Craft (2001), who were interested in afterbody flows (esp. the under-expanded jet issuing from the rear of an aircraft/missile). This work applies the current state of the art in realizable, compressibility-modified, second-moment closures to this flow, and demonstrates the superiority of this method over traditional second-moment closures. However, the nature of this application assumes that the jet-body itself is in motion, and hence, that the jet is not issuing into quiescent surroundings. Therefore this work has not been chosen as a test-case here.
2.2 Studies on which this UFR review will be based
The following works have been chosen as being the most appropriate, currently available, information on which comparisons have been made between CFD and experiment, and they represent a very good match for what is required for this UFR :
- Cumber et al. (1994) present a comparison between CFD and experiment for the case of a moderately under-expanded jet, applying two turbulence models: a standard, and a modified, version of the k-ε scheme.
- A second paper, Cumber et al. (1995) presents further comparison between CFD and experiment, using the same turbulence models as previously, but this time considering their application to the highly under-expanded jet. Details of the turbulence models, discretisation schemes, boundary conditions, and computational mesh are given.
- Very recently, Bartosiewicz et al. (2002) present results using a second-moment closure methodology, for the cases of both the moderately and highly underexpanded jet. Their results are, usefully, based on the same experimental work as studied by Cumber (above), and they also cross-plot their results with a modeling study of the same problem by Pao and Abdol-Hamid (1996), who used similar modeling to that of Cumber.
The above CFD work is compared with several experimental studies, for both the near-field (in the under-expanded region) and in the far-field. However, the focus of this UFR lies purely in the near field, since far-field behaviour is considered elsewhere in other UFR documentation. This still leaves us, however, with two good quality experimental studies with which both Cumber’s, and Bartosiewicz’s CFD work has been compared, covering the near-field behaviour of both moderately- and highly- under-expanded jets. Although neither of these experiments, apparently, were performed with CFD validation in mind, this should not affect their suitability for use here :
• Seiner & Norum (1979,1980) performed experiments on supersonic jets emerging from a convergent-divergent nozzle, and an exit Mach number of M=2. Data is available showing the radial values of Mach number, the axial velocity, and the axial pressure. This work is used by Cumber et al. (1994) on studies of the moderately under-expanded jet, and by Bartosiewicz (2002).
It is worth noting, however, that the latter paper (Bartosiewicz, 2002) attributes this experimental work on moderately underexpanded jets to that of Dash, Wolf and Seiner (1985). However, examination of the paper (actually Seiner, Dash & Wolf, 1985) reveals that the original source of the data is in fact Seiner and Norum (1979, 1980). Hence, we find that the CFD work of Bartosiewicz et al. (2002) is actually compared with the same experimental data as that of Cumber et al. (1994).
• For the highly underexpanded jet, the CFD studies from Cumber et al. (1995) and Bartosiewicz et al. (2002) both compare their work with the experiments of Donaldson & Snedecker (1971). Although Donaldson and Snedeker were primarily interested in impinging jets, they also provide data for a free axis-symmetric jet issuing from a convergent nozzle, for a variety of pressure ratios from a subsonic jet (P0/P∞ = 1.25), to a highly under-expanded jet (P0/P∞ = 6.76), showing the radial velocity profiles measured using a Pitot-static pressure probe.
© copyright ERCOFTAC 2004
Contributors: Chris Lea - Health & Safety Laboratory