AC 6-07 Evaluation

Front Page

Description

Test Data

CFD Simulations

Evaluation

Best Practice Advice

Draft tube

Application Challenge 6-07               © copyright ERCOFTAC 2004

Evaluation

Comparison of CFD Results and Test data

Both workshops used (r) as BC but (n) is currently the most complete test case. It is therefore recommended that future calculations use the (n)-set of data for each case for comparisons with the experiments. However, if the purpose is e.g. to validate a new code or for some other reason compare with other computations the (r)-set of data is still recommended.

Thus, data presented here are all based on computations using the (r) inlet boundary condition for both the T test case and the R test case. Comparison of CFD with test data may be qualitative (e.g. scatter plots, contour plot comparison) or quantitative (statistical measures, e.g. mean bias and variance). Particular focus is given to comparisons between measured and calculated [../../help/glossary.htm DOAP]s. All data discussed here are available in the Proc-W2.

Engineering Quantities and DOAP:s

The results on engineering quantities, calculated by the contributors themselves, for both the T and the R test cases, are presented in Table 4.1.

In Table 4.2. is presented the engineering quantities for all computations, evaluated in a uniform way as described in Proc-W2, Appendix C1. Table 4.3 shows the major design and assessment parameters ([../../help/glossary.htm DOAP]:s) from experiment and simulations. Figure 4.1 present the results in graphical form.

Discussion

A comparison between results in Tables 4.1 and 4.2 shows immediately, in some cases, large difference in computed results, depending on how the engineering parameters are estimated (how extrapolation to the wall is carried out, etc.), and the code used. This is particularly important for Cp_r,wall and ζ.

It is also clear that there is a large difference between computed Cp_r,wall and Cp_r,average. The reason for this latter discrepancy is the following: Radial pressure distributions, experimentally determined and computedcurves, in CSIa, were shown in Proc.T99W2, Part2, pp.55-58. For the experimental profile, see also Andersson (2003b), fig.19.

An analysis of these figures clarifies the main reason for the large values of Cp_r,wall, and also for the large scatter in Cp_r,wall:

The computed radial pressure distributions generally fall of sharply near the outer wall whereas the experimental distributions exhibit a sharp rise in pressure in this region, followed by a very small decrease just at the wall. The computed wall pressures at CSIa are therefore much lower than the average pressure over the same cross-section. Cp,_wall is thus dominated by the wall-value, which is not representative for the average pressure. Using the average or average pressure over the inlet cross-section therefore gives a much more representative (and lower) Cp_r, as shown in Table 4.2. (generally Cp_r,_wall is 1.14-1.66, and Cp_r,average is 0.89-0.99).

The main reason for this difference in radial pressure distribution is that the grid in this region is not fine enough and that it does not represent the true surface geometry sufficiently accurate. Evidence of this can be found in Proc.T99W2, paper by Jonzén et al. (2003), Table 2, where a much finer grid than the standard grid recommended by the organizers, gave a difference in Cp_r,wallof -0.12, that is, a 10 % decease in Cp_r,wall. So, in spite of the relatively fine grid that was proposed by the organizer, it is found that this grid is still too coarse, particularly near the inlet.

For the remaining discussion we will focus on the results of Table 4.3 and Figure 4.1, which show the major design or assessment parameters taken from computations (recalculated by the organizers) and the corresponding experimental values.

It is clear that the scatter in computed Cp_r,average is much smaller than in Cp_r,wall. This fact, together with the discussion above, shows that Cp_r,average is a much more suitable DOAP than Cp_r,wall. Table 4.3 also shows that the computed values of Cp_r,average are lower than the experimentally determined value, the difference being larger that the estimated uncertainty. Thus, the difference is significant. The reason for this discrepancy is discussed further in section 4.2.1.

From Table 4.3 and Figure 4.1 one can also see that the computed energy-loss coefficient (ζ) shows a surprisingly large scatter and also that the experimental value has a very large uncertainty, Andersson, (2003a). There are several reasons for the large scatter in (ζ): It is an ill-conditioned quantity since it comes out as the difference between two (almost equal) large numbers, (see eq. 9) and the uncertainty in Cp thus has a large effect on (ζ). The experimental value also has a large uncertainty, mainly for the same reason. Also, quantities which could not be measured are determined as a best estimate from the computed result. So, in spite of the effort made, it seems to be very difficult to obtain an accurate experimental determination of (ζ).

Table 4.1 Engineering quantities, calculated by the contributors. (from Proc.T99W2, part 2, p.5)

ACRONYM											Remark
CASE T	Cp	ζ	αax, Ia	αax, III	αsw, Ia	αsw, III	β, Ia	β, III	S, Ia	S, III
AEAT keps	1,1300	0,0830	1,0180	1,1700	0,0690	0,0640	1,0760	1,1250	0,0460	0,0430
CKD keps	1,1606	0,1044	0,9986	1,1702	0,0588	0,0121	1,0602	1,1089	0,1865	0,0605
HQ-FIDAP keps	1,7460	0,1050	1,0300	1,3150	0,0560	0,0270	1,0800	1,1470	0,2920	-0,0870
HQ-FINE keps	1,1040	0,1590	1,0300	1,0900	0,0560	0,0500	1,0800	1,1360	0,2930	-0,1290
HQ-TASC keps	1,3940	0,0910	1,0300	1,2220	0,0560	0,0490	1,0800	1,1400	0,2920	-0,1320
HTC keps	1,2500	0,1250	1,0260	1,4620	0,0670	0,0410	1,0770	1,2140	0,2860	0,1080
NUT keps	1,2730	0,0690	1,0100	1,2520	0,0590	0,0190	1,0720	1,1240	0,3070	0,0800
TEV keps	1,2330	0,1410	1,0040	1,2180	0,0570	0,0740	1,0540	1,1110	0,3020	0,2570
VUAB keps	1,2946	0,0870	1,0239	1,2360	0,0580	0,0091	1,0771	1,1029	0,3024	-0,2018	Values are from recalculation by F. Engström.
LTU keps	1,2880	0,0570	1,0381	1,2226	0,0596	0,0594	1,0889	1,2244	0,1772	0,1506	Corrected value for Cp wall
Iowa keps	1,1950
Experiment T	1,120	0,09	1,040	1,090	0,060	0,040	1,110	1,020	0,310		αsw III, without vertical comp.
											β III, only axial comp.
CASE R	Cp	ζ	αax, Ia	αax, III	αsw, Ia	αsw, III	βIa	βIII	S, Ia	S, III
CKD realizable-keps 2	1,1608	0,1047	0,9980	1,1475	0,0299	0,0075	1,0327	1,0849	0,1034	0,0333
HQ-FIDAP keps 2	1,7980	0,0920	1,0280	1,1940	0,0290	0,0190	1,0520	1,0920	0,1570	-0,0680
HQ-FINE keps 2	1,1200	0,1690	1,0270	1,2220	0,0280	0,0330	1,0510	1,1210	0,1570	-0,0450
HQ-TASC keps 2	1,4050	0,0920	1,0280	1,2090	0,0290	0,0450	1,0520	1,1260	0,1570	-0,0620
HTC cubic-keps 2	0,9950	0,2050	1,0240	1,4750	0,0390	0,0300	1,0480	1,2160	0,2370	0,0610
HTC quadratic-keps 2	0,9510	0,2480	1,0240	1,4500	0,0390	0,0390	1,0480	1,2200	0,2370	0,0490
NUT keps 2	1,0750	0,0700	1,0080	1,3540	0,0290	0,0260	1,0400	1,1820	0,1640	0,0850
TEV rsm 2	1,2080	0,1250	1,0030	1,2930	0,0280	0,0130	1,0300	1,1230	0,1630	0,0250
VUAB keps 2											Resimulated after workshop, no data available
LTU keps 2	1,3971	0,0586	1,0332	1,1875	0,0307	0,0524	1,0584	1,1487	0,0964	0,0879
Iowa keps 2	1,2365										different ε
Iowa komega 2	1,2273										different ε
VUAB keps 3											Resimulated after workshop, no data available
CKD rsm 3	1,0420	0,1230	0,9854	1,2531	0,0291	0,0074	1,0195	1,1332	0,1024	0,0009
EXA vl 3	1,1880	0,1480	1,0100	1,2360	0,0280	0,0450	1,0000	1,0840	0,0950
HTC LES 3	0,9370	0,2170	1,0850	1,8000	0,0470	0,0900	1,1080	1,3700	0,2600	0,0700
NUT LES 3	1,0900		1,0080	1,1630	0,0290		1,0400	1,1210	0,1640
Experiment R	1,09		1,040		0,030		1,080		0,170

Table 4.2. Engineering quantities, recalculated by the organizers (from Proc.T99W2, part 2, p. 17)

ACRONYM												Remark
CASE T	Cpr,wall	Cpr,average	ζ	αax, Ia	αax, III	αsw, Ia	αsw, III	βIa	βIII	S, Ia	S, III
AEAT	1,361	0,952	0,150	1,038	1,210	0,059	0,036	1,093	1,140	0,302	-0,087
NUT	1,262	0,925	0,043	1,023	1,234	0,059	0,010	1,079	1,104	0,308	-0,227
TEV	1,276	0,963	0,050	1,024	1,201	0,058	0,025	1,077	1,119	0,301	-0,131
HTC	1,250	0,916	0,172	1,042	1,270	0,056	0,009	1,091	1,117	0,293	-0,205
VUAB	1,295	0,917	0,087	1,024	1,236	0,058	0,009	1,077	1,103	0,302	-0,202
CKD	1,185	0,892	0,110	1,019	1,276	0,059	0,009	1,076	1,119	0,305	-0,252
HQ-FIDAP	1,665	0,921	0,120	1,037	1,325	0,056	0,016	1,089	1,152	0,292	-0,105
HQ-FINE	1,144	0,991	0,077	1,037	1,219	0,056	0,034	1,088	1,142	0,293	-0,094
HQ-TASC	1,397	0,956	0,152	1,037	1,230	0,056	0,035	1,089	1,145	0,292	-0,145
Iowa	1,195	0,887	0,162	1,037	1,347	0,059	0,011	1,093	1,151	0,302	-0,108
LTU	1,537	0,980	0,066	1,034	1,144	0,059	0,030	1,082	1,106	0,302	-0,037
CASE T	Area Ia	Area III	Area IVb	Q Ia	Q III	Q IVb	Q III/Q Ia	Q IVb/Q Ia	αtotal, Ia	αtotal, III	αtotal, IVb
AEAT	0,145	0,520	1,065	0,519	0,513	0,511	0,989	0,984	1,107	1,277	2,308
NUT	0,145	0,518	1,064	0,503	0,509	0,511	1,013	1,017	1,094	1,257	2,888
TEV	0,145	0,520	1,064	0,515	0,517	0,518	1,004	1,006	1,092	1,251	2,516
HTC	0,145	0,520	1,065	0,518	0,515	0,512	0,993	0,988	1,107	1,292	3,022
VUAB	0,145	0,522	1,064	0,514	0,516	0,517	1,005	1,007	1,092	1,258	2,842
CKD	0,145	0,520	1,064	0,509	0,510	0,510	1,002	1,003	1,089	1,295	3,343
HQ-FIDAP	0,145	0,521	1,064	0,522	0,522	0,522	1,000	0,999	1,102	1,366	3,730
HQ-FINE	0,145	0,521	1,064	0,521	0,522	0,517	1,001	0,991	1,102	1,285	3,235
HQ-TASC	0,145	0,521	1,064	0,522	0,516	0,515	0,989	0,986	1,102	1,294	2,487
Iowa	0,145	0,520	1,064	0,509	0,508	0,506	0,999	0,994	1,106	1,381	3,049
LTU	0,145	0,520	1,065	0,516	0,519	0,518	1,005	1,003	1,103	1,200	1,967

Table 4.3. Major design and assessment parameters ([../../help/glossary.htm DOAP]:s).

CASE T	Cpr,wall	Cpr,average	ζ
AEAT	1,361	0,952	0,150
NUT	1,262	0,925	0,043
TEV	1,276	0,963	0,050
HTC	1,250	0,916	0,172
VUAB	1,295	0,917	0,087
CKD	1,185	0,892	0,110
HQ-FIDAP	1,665	0,921	0,120
HQ-FINE	1,144	0,991	0,077
HQ-TASC	1,397	0,956	0,152
Iowa	1,195	0,887	0,162
LTU	1,537	0,980	0,066
Experiment T	1,12 + 0,02 - 0,01	1.06 + 0,04 - 0,02	0,09 + 0,06

Figure 4.1 Major design and assessment parameters

Velocity Field

Table 4.4 shows differences in results between calculations and experiments in CS II and III. Briefly, two fields (e.g. U-velocity), one field obtained from experiments and the other one obtained from computations, are compared on the same grid, and the standard deviation or RMS value and Mean value, Max and Minimum values are computed. By this method, we get a comparison of the whole field and also a quantitative measure of the difference between the fields (the Stdv).

Figure 4.2. Normalised axial velocity at the horizontal mid-plane of CS II. (-Mean value of CFD-calculations T99 W2; : Max /min value from CFD simulations T99 W2; + VUAB CFD simulation; x Experiment)

In Figure 4.2 one can see that there is a rather good agreement between the different CFD-calculations for test case T, comparing the (normalised) axial velocity. The mean variation is ± 0.04 for the CFD-calculations at each point of the mid-plane of the calculations. However, in the worst regions the differences are as high as ± 0.15. The results from VUAB (+) is also included, to show how a single computation behaves along the profile. Compared with Experiments (x), there is a significant difference in the resulting profile, that cannot be explained by the variation between CFD-calculations or experimental uncertainties.

An illustrative way of showing the accuracy of the simulations relative to the measured veloctiy values is shown in Figure 4.3 where the difference between the simulations and the experiments are shown. The difference is defined as U_exp/U_{exp, average} – U_sim/U_sim,average

Figure 4.3: Difference plot of the axial velocity at cross section II. From Cervantes & Engström

In Proc-W2, Appendix C2 are collected the difference plots for some selected simulations. It is seen that the general feature of two minima are similarly determined among the contributions, and that the maximum deviations are large (30%).

An quantitative integral measure of the accuracy of these calculations can be defined as the standard deviation of the data integrated over the cross section. The result of such calculations is collected in Figure 4.4 and in Table 4.4.

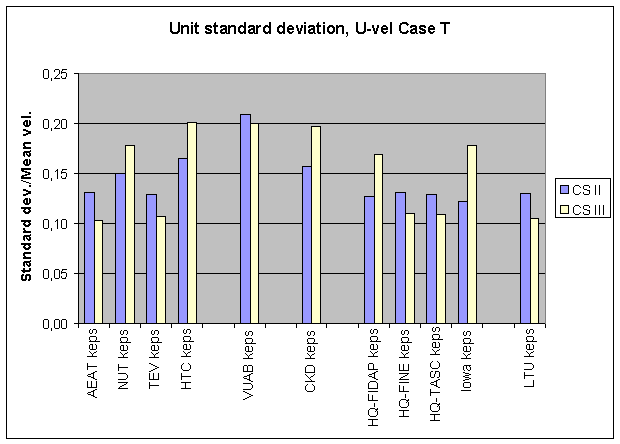Figure 4.4: Standard deviation of velocity difference integrated over cross sections II and III.

Table 4.4 Comparisons between computations and experiments at CS II and III

Discussion of Scatter in Design or Assessment Parameters

and ζ)

In the results collected, it is noticed that the two key engineering quantities, C_p and ζ, are subject to considerable scatter among the contributions. Part of the scatter is due to the post-processing of data, but other factors also contribute, as will be discussed here.

From the figures of the radial pressure distribution at section Ia (Figure 3 in Proc-W2) the reason for the large values of C_p,wall, and also its large scatter, is explained by the observation that the computed radial pressure distributions generally fall off sharply near the outer wall, whereas the experimental distribution show a sharp rise in this region, followed by a small decrease as the wall is approached. The computed wall pressure levels at CS Ia are therefore much lower than the average pressure over the same cross-section. Using the average pressure over the inlet cross-section therefore gives a more representative (and lower) value of C_p. (C_p,wall is in the range 1.14 -1.66 and C_p,average in the range 0.89-0.99).

An explanation for the scatter in the radial pressure distribution at CS Ia may be that the grid in this region is not fine enough to resolve the rapid evolution of the pressure and that it does not represent the surface geometry accurately enough. From the (inviscid) equation for the radial pressure,

it is noticed that a large contribution to the radial pressure gradient comes from the second term even in regions where the streamwise gradient is moderate because of the magnitude of u_ax. A finer resolution of this region may result in a 10% reduction of the C_p,wall-value as demonstrated by Jonzén et al.

The scatter in the loss coefficient may be due to at least two reasons. In the expression for ζ, (9), the last term is close to unity, and the second is small (the area ratio is small) which means that the evaluation of ζ is ill-conditioned despite the accuracy in C_p'. This indicates that the use of ζ as a key parameter to evaluate gains in efficiency from e.g. a geometry optimisation may be risky unless a reconditioning of the calculations can be done. To validate such a gain experimentally, may be even more difficult since not all of the α-values are available experimentally. From the experimental results it has been deduced that ζ = 0.09 (+0.06/-0.07) which illustrates the difficulty encountered in this evaluation.

A second source of uncertainty in ζ emanates from the use of wall-functions for the near-wall calculations. Since it is expected that most flow losses occur in this region, and in fact will be reflected in the pressure results, a more careful evaluation based on the energetics associated with the wall functions could be recommended as a separate method to determine ζ. A further factor adding to the losses is also the periodic character of the flow, most notable at the runner.

Conclusions and Recommendations

The most important results and suggestions of the workshop are summarised below.

•        The 700k computational grid suggested by the organisers turns out to be too coarse, particularly near the inlet section, where it has a large effect on computed pressure recovery C_p,wall . This is caused by the fact that the pressure gradients in both the axial and radial directions are large and must be resolved properly.

•        The uncertainty in the experimentally determined energy-loss factor is large because it is an ill-conditioned quantity, to a large extent determined by C_p.

•        It was found that the y⁺ criterion for wall functions was violated in many regions of the flow.

•        The importance of complete and well-defined inlet boundary conditions is highlighted in many of the workshop contributions.

•        The pressure recovery coefficient C_p,average , based on the average pressure over the inlet cross-section, is a suitable assessment parameter, which for Case T is calculated with a scatter of about + 5%. The difference between computed and experimentally determined C_p,average, is statistically significant.

•        Computations of Case T by different groups but with the same mesh, inlet- and outlet boundary conditions, and turbulence model, generally give very similar results. Thus, the “Quality” in the concept of “Quality and Trust”, is not too far away.

•        Because of the abovementioned weaknesses, it has, so far, not been possible to draw conclusions about the influence of turbulence model on the solution.

Suggestions for further computational and experimental work are given below:

•        For further computational work, as a first step, a much finer grid must be constructed, particularly near the inlet. This is necessary also when using wall functions.

•        As step 2, it is recommended that the wall functions should be replaced by suitable near-wall models.

•        Since more than 80 % of the pressure recovery takes place in the first 10 % or so of the draft tube length (the draft tube cone), more detailed (axial and radial) pressure and velocity measurements are required.

•        Also, complete 3-component velocity measurements in some cross sections are highly desirable.

These suggestions are directed towards increasing the quality of the computed solutions and increasing the accuracy of the experimentally determined engineering parameters, thus increasing the value and usefulness of the draft tube test case.

References

Bergström, J. (2000). “Modeling and Numerical Simulation of Hydro Power Flows”. Doctoral Thesis 2000-06, Luleå University of Technology, Department of Mechanical Engineering, Division of Fluid Mechanics.

Casey M. & Wintergerste T. (editors). (2000) ERCOFTAC Best Practice Guidelines. ERCOFTAC Special Interest Group on “Quality and Trust in Industrial CFD.

Gebart B.R., Gustavsson L.H. & Karlsson R.I. (editors) (2000a) "Turbine 99 – Workshop on Draft Tube Flow”. Technical Report 2000-11, Luleå University of Technology, Department of Mechanical Engineering, Division of Fluid Mechanics. ISSN:1402-1536

Gebart B.R., Gustavsson L.H. & Karlsson R.I. (2000b) "Report from Turbine 99 – Workshop on Draft Tube Flow in Porjus, Sweden, 20-23 June 1999”. Paper presented at the 20^th IAHR Symposium Hydraulic Machinery and Systems. Aug. 6-9, 2000, Charlotte, North Carolina, U.S.A.

Engström T.F., Gustavsson L.H. & Karlsson R.I. (2002) "Report from Turbine 99 – Workshop 2 on Draft Tube Flow”. The second ERCOFTAC Workshop on Draft Tube Flow, held in Älvkarleby, Sweden, June 18-20, 2001. Paper presented at the 21^st IAHR Symposium Hydraulic Machinery and Systems, Lausanne, Switzerland, Sept. 2002

Engström, T.F., Gustavsson, L.H., & Karlsson, R.I. (2003), Proceedings of Turbine-99 - Workshop 2. The second ERCOFTAC Workshop on Draft Tube Flow. Älvkarleby, Sweden, June 18-20 2001. Available on the web, http://www.sirius.luth.se/strl/Turbine-99/index.htm

Andersson U. (2003a) Turbine 99 – Experiments On Draft Tube Flow (Test Case R) In: Proceedings from Turbine 99 – Workshop 2, Engström et al. (editors) (2003).

Andersson U. (2003b) Test Case T – some new results and updates since Workshop I. In: Proceedings from Turbine 99 – Workshop 2, Engström et al. (editors) (2003).

Jonzén S, Hemström B, Andersson U (2003) “Turbine 99- Accuracy in CFD simulations on draft tube flow” (2003). In Proceedings from Turbune 99 – Workshop 2, Engström et al. (editors) (2003).

© copyright ERCOFTAC 2004

---

Contributors: Rolf Karlsson - Vattenfall Utveckling AB Front Page Description Test Data CFD Simulations Evaluation Best Practice Advice