UFR 4-02 Test Case: Difference between revisions
m (Dave.Ellacott moved page Silver:UFR 4-02 Test Case to UFR 4-02 Test Case over redirect) |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 95: | Line 95: | ||
The inlet boundary conditions were set equal to the measured profiles at x/R<sub>i </sub>= 0.1 (see Figure 2.), however, for [[Image:U4-02d32_files_image021.gif]] = 0.1 profiles were extrapolated from the downstream profiles. Radial [[Image:U4-02d32_files_image022.gif]] and azimuthal [[Image:U4-02d32_files_image023.gif]] turbulence intensities were estimated as [[Image:U4-02d32_files_image025.gif]] and [[Image:U4-02d32_files_image027.gif]] respectively at the inlet, and in absence of other information, the mean radial velocity and turbulent shear stresses were set equal to zero. At the outlet, the mean axial velocities were prescribed to be equal measured data at x/R<sub>i</sub> = 8.92, and the zero normal gradient conditions were assumed for all other variables. | The inlet boundary conditions were set equal to the measured profiles at x/R<sub>i </sub>= 0.1 (see Figure 2.), however, for [[Image:U4-02d32_files_image021.gif]] = 0.1 profiles were extrapolated from the downstream profiles. Radial [[Image:U4-02d32_files_image022.gif]] and azimuthal [[Image:U4-02d32_files_image023.gif]] turbulence intensities were estimated as [[Image:U4-02d32_files_image025.gif]] and [[Image:U4-02d32_files_image027.gif]] respectively at the inlet, and in absence of other information, the mean radial velocity and turbulent shear stresses were set equal to zero. At the outlet, the mean axial velocities were prescribed to be equal measured data at x/R<sub>i</sub> = 8.92, and the zero normal gradient conditions were assumed for all other variables. | ||
[[Image:U4-02d32_files_image029.gif]] LES calculations of the swirling jets were performed by Schlüter et al. [12]. The cross section of the test rig of | [[Image:U4-02d32_files_image029.gif]] LES calculations of the swirling jets were performed by Schlüter et al. [12]. The cross section of the test rig of Egly’s experiment [13] calculated by Schlüter, with the location of the measured profiles are depicted on Figure 3. To simplify computational geometry, the inlet face was located just behind the trailing edges of the swirler. Instead of including swirler geometry, the swirl was imposed as a boundary condition at the inlet to the computational domain. The velocity profiles at the inlet have to be adjusted to match the first measured profile performed in the experiment, however, since no measurement data are available directly behind the trailing edges of the swirler, velocity profiles were approximated from the 2D axisymmetric computations. | ||
An eddy viscosity approach was used for subgrid scales: | An eddy viscosity approach was used for subgrid scales: | ||
| Line 103: | Line 103: | ||
with Filtered Smagorinsky model [16] defined on a high-pass filter HP to determine the eddy viscosity ν<sub>t</sub> | with Filtered Smagorinsky model [16] defined on a high-pass filter HP to determine the eddy viscosity ν<sub>t</sub> | ||
<center>[[Image:U4-02d32_files_image033.gif]] </center> with ''c<sub>2</sub>'' = 0.37 | <center>[[Image:U4-02d32_files_image033.gif]] </center> | ||
which offers an improved behaviour in transitional flows | with ''c<sub>2</sub>'' = 0.37 which offers an improved behaviour in transitional flows over the standard Smagorinsky model. | ||
The results show that fully 3D calculations generally stay in very good agreement with experiment for all parameters, while 2D axisymmetric predictions do not correlate at all with experimental data. However, even fully 3D calculations slightly underpredict axial velocity fluctuations and same deviations of profiles of circumferential velocity component can be observed. | The results show that fully 3D calculations generally stay in very good agreement with experiment for all parameters, while 2D axisymmetric predictions do not correlate at all with experimental data. However, even fully 3D calculations slightly underpredict axial velocity fluctuations and same deviations of profiles of circumferential velocity component can be observed. | ||
| Line 118: | Line 118: | ||
{{UFR|front=UFR 4-02|description=UFR 4-02 Description|references=UFR 4-02 References|testcase=UFR 4-02 Test Case|evaluation=UFR 4-02 Evaluation|qualityreview=UFR 4-02 Quality Review|bestpractice=UFR 4-02 Best Practice Advice|relatedACs=UFR 4-02 Related ACs}} | {{UFR|front=UFR 4-02|description=UFR 4-02 Description|references=UFR 4-02 References|testcase=UFR 4-02 Test Case|evaluation=UFR 4-02 Evaluation|qualityreview=UFR 4-02 Quality Review|bestpractice=UFR 4-02 Best Practice Advice|relatedACs=UFR 4-02 Related ACs}} | ||
Latest revision as of 13:58, 12 February 2017
Confined coaxial swirling jets
Underlying Flow Regime 4-02 © copyright ERCOFTAC 2004
Test Case
Brief description of the study test case
Schematic drawing of the flow is shown on the Figure 2. Measurements were carried out in two groups for coswirling and counterswirling jets with different swirl numbers and jets velocities. The inner jet was issued from coaxial stainless steel tube and axially shifted several millimetres into the test section. The experiment was performed in two configurations, with outer jet being in coswirl and counterswirl versus inner jet. For inner jet swirl was generated by swirler with 12 fixed vanes, while for the outer annular one swirling motion was generated by swirler with 24 adjustable vanes. The adjustment of outer vanes allowed achievement of co- and counterswirl conditions.
The experiment chosen was also calculated with various turbulence models. Sharif & Wong [5] tested three models: nonlinear k-ε (NKEM), differential Reynolds stress transport (RSTM) and standard algebraic stress model (ASTM), and showed that RSTM and ASTM better predict mean flow fields that NKEM.
The Wu and Gouldin experiments may be regarded as classic cases and have been extensively studied by several investigators. The detailed study of that case was performed by Srinivasan and Mongia [21] and followed by Sturgess [22] who gave a special attention to formulating of inlet boundary conditions.
Test Case Experiments
The measurements were performed in two groups of experiments. In the first group, mean flow measurements were made with a directional Pitot probe, to determine the influence of outer swirl on the size of the recirculation zone and on the magnitude of the reverse flow velocity. In the second group, the detailed measurements of mean flow and turbulence properties for one coswirl and one counterswirl conditions were undertaken.
In the coswirl experiment the swirl numbers were Si=0.58 and So=0.54 for inner and outer jets respectively. Mean axial velocities were about 29.6 m/s and 20.3 m/s for inner and outer jet respectively, and the Reynolds number based on the inner jet mean velocity and diameter of the combustor was about Re = 1.7 · 105. It was investigated from the Pitot probe and hot-wire measurements at the Re = 170000 and Re = 250000 that the flow field parameters are Reynolds number independent.
In the counterswirl experiment the swirl numbers were Si=0.49 and So=-0.51 for inner and outer jets respectively. Mean axial velocities were about 30.3 m/s and 20.2 m/s for inner and outer jet respectively, and the Reynolds number calculated similarly was also about 170000.
Experimental setup is presented in details in Vu & Gouldin[8]. As shown in Figure 2. the swirl combustor is an acrylic pipe of diameter 2·R0 = 145 mm, with two coaxial swirling jets issuing into the combustor. The coaxially placed inner jet tube has inner and outer diameters:
2·Ri = 34.3 mm and 2 (Ri + δ) = 38.6 mm respectively, for the first group of experiments and
2·Ri = 37.2 mm and 2 (Ri + δ) = 38.1 mm respectively, for the second group of experiments,
where δ is a thickness of the inner tube wall.
Inner jet swirl generator is placed 152mm upstream of the inner jet exit during the Pitot measurements and 122 mm during the hot-wire ones and consists of 12 equally spaced vanes placed in the annular volume between a center tube and an outer casing. The swirl direction of a outer jet can be adjusted to achieve coswirl and counterswirl conditions relative to the inner jet. The swirl number S is the ratio of angular to the axial momentum flux defined for the inner jet and outer annular jet respectively as:
Where Ux , Uθ — axial and circumferential velocities.
The quantities measured during the experiment were:
- axial and azimuthal velocities u and w
- static pressure p
- turbulence dissipation rate ε
Unfortunately there are no measurements at the exit from the inner tube ( x=0 ). The measured profiles for velocities and pressure are provided for a range of x/Ri from 0.1 to 8.92, where x is the axial distance from the exit of the inner jet and Ri is the inside radius of the inner jet tube. For the profiles of turbulence intensity and dissipation measurements data are provided for a range beginning from x/Ri=0.52.
As it was mentioned above, the measurement data were acquired with directional five-hole Pitot probe and linearized constant temperature hot-wire anemometer. High velocity gradients and turbulence levels contribute to uncertainty in axial and tangential velocity measurements. To assess accuracy, average speeds measured by hot-wire and Pitot probe were compared, and in the regions of local fluctuations less then 30 to 40% the agreement within ±10% was obtained, while much better ±2% agreement was achieved where turbulence levels are low and gradients are not severe.
For turbulence intensity measurements, an error analysis shows that errors can exceed 10% for intensities above 20-30% and for higher levels of turbulence it rapidly grows.
The detailed error analysis can be found in [8].
CFD Methods
Although many publications have been provided on calculations of swirling confined coaxial flows just a few have used LES due to limits in computer resources, however, using LES the large vortical structures of the flow are resolved leading to a much better insight into the flow features. CFD calculations of these flows concentrate mainly on comparison and analysis of various turbulence models for prediction of flow field parameters. Standard k-ε model is widely used for simple flow cases but it is not adequate for complex recirculating or swirling flows involving streamline curvature and rotation. To improve predictions, many modifications of k-ε have been employed, such as ones based on Richardson correction, multiple-scale k-ε or nonlinear k-ε NKEM. CFD results showed that modified models were better than standard k-ε, however, significant differences between numerical and experimental results still existed.
Lei et al. [1] calculated the flow type considered with, proposed and developed by them, a new ASM model and its simplified explicit form [14]. The new ASM accounts for the stress production, dissipation, redistribution, and partially convective transport of Reynolds stresses due to swirl-turbulence interactions.
The numerical solution was obtained using finite difference approach and the iterative procedure adopted the SIMPLE algorithm. The hybrid difference schemes were employed for discretisation of convection and diffusion terms, and the resultant equations were calculated with underrelaxation TDMA line-by-line sweeping technique. The computations were performed with CCVC (Coal Combustion in Vortex Chamber) software developed for simulating swirling turbulent flow, heat transfer and combustion.
The measured velocity profiles and uniform distributions for other variables were used as the inlet conditions. The wall function was used for calculating wall shear stresses at the grid nodes adjacent to the walls. At the outlet from the calculation domain, axial gradient were assumed to be zero for all variables. Zero radial gradient was imposed also on the combustor axis for all variables except radial and tangential velocities which are zero. The grid system consisted of 25 x 24 grid nodes and was found that results were grid independent.
Sharif & Wong [5] applied ASM model[15] where equations for the Reynolds stresses were derived from its transport equations assuming that the transport ![]() with the proportionality factor
with the proportionality factor ![]()
An explicit time-marching procedure, based on the Marker and Cell (MAC) method was used in the numerical procedure, while the convection terms in the governing transport equations were discretized using a bounded directional transportive upwind differencing scheme. The scheme was bounded by the flux-corrected-transport algorithm of Zalesak [23].
The standard wall function for the nodes next to solid wall was used as a boundary condition. At the wall, zero normal gradient for k was imposed. At the symmetry axis, zero normal gradient was assumed for all variables except azimuthal velocity and the Reynolds shear stresses, which were set to be equal zero.
The inlet boundary conditions were set equal to the measured profiles at x/Ri = 0.1 (see Figure 2.), however, for ![]() = 0.1 profiles were extrapolated from the downstream profiles. Radial
= 0.1 profiles were extrapolated from the downstream profiles. Radial ![]() and azimuthal
and azimuthal ![]() turbulence intensities were estimated as
turbulence intensities were estimated as ![]() and
and ![]() respectively at the inlet, and in absence of other information, the mean radial velocity and turbulent shear stresses were set equal to zero. At the outlet, the mean axial velocities were prescribed to be equal measured data at x/Ri = 8.92, and the zero normal gradient conditions were assumed for all other variables.
respectively at the inlet, and in absence of other information, the mean radial velocity and turbulent shear stresses were set equal to zero. At the outlet, the mean axial velocities were prescribed to be equal measured data at x/Ri = 8.92, and the zero normal gradient conditions were assumed for all other variables.
 LES calculations of the swirling jets were performed by Schlüter et al. [12]. The cross section of the test rig of Egly’s experiment [13] calculated by Schlüter, with the location of the measured profiles are depicted on Figure 3. To simplify computational geometry, the inlet face was located just behind the trailing edges of the swirler. Instead of including swirler geometry, the swirl was imposed as a boundary condition at the inlet to the computational domain. The velocity profiles at the inlet have to be adjusted to match the first measured profile performed in the experiment, however, since no measurement data are available directly behind the trailing edges of the swirler, velocity profiles were approximated from the 2D axisymmetric computations.
LES calculations of the swirling jets were performed by Schlüter et al. [12]. The cross section of the test rig of Egly’s experiment [13] calculated by Schlüter, with the location of the measured profiles are depicted on Figure 3. To simplify computational geometry, the inlet face was located just behind the trailing edges of the swirler. Instead of including swirler geometry, the swirl was imposed as a boundary condition at the inlet to the computational domain. The velocity profiles at the inlet have to be adjusted to match the first measured profile performed in the experiment, however, since no measurement data are available directly behind the trailing edges of the swirler, velocity profiles were approximated from the 2D axisymmetric computations.
An eddy viscosity approach was used for subgrid scales:
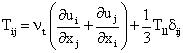
with Filtered Smagorinsky model [16] defined on a high-pass filter HP to determine the eddy viscosity νt
with c2 = 0.37 which offers an improved behaviour in transitional flows over the standard Smagorinsky model.
The results show that fully 3D calculations generally stay in very good agreement with experiment for all parameters, while 2D axisymmetric predictions do not correlate at all with experimental data. However, even fully 3D calculations slightly underpredict axial velocity fluctuations and same deviations of profiles of circumferential velocity component can be observed.
Pierce & Moin [19] performed LES calculations of experiment of Roback & Johnson [18] and Sommerfeld et al. [20]. The grid system consisted of 226 x 163 x 128 grid nodes and 250 x 125 x 64 nodes for calculations of Sommerfeld et al and Roback & Johnson respectively. The numerical scheme consisted of conservative, second-order finite-volumes on staggered grid. Subgrid-scale mixture fraction in the limit of fast chemistry was modelled by a presumed PDF approach. To compute the variance of the subgrid mixture fraction as input to the presumed PDF the new dynamic model was used. Their LES calculations showed that velocity and concentration profiles are in good agreement with experiments. However, they noticed meaningful sensitivity on the exit boundary conditions and moreover that heat release reduces mixing and accelerate the flow in the combustor.
© copyright ERCOFTAC 2004
Contributors: Stefan Hohmann - MTU Aero Engines

