UFR 3-03 Test Case: Difference between revisions
m (Dave.Ellacott moved page Gold:UFR 3-03 Test Case to UFR 3-03 Test Case over redirect) |
|||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 18: | Line 18: | ||
The testcase geometry is shown in Figure 2. It consists of an axisymmetric diffuser with an internally mounted cylinder along the centreline. In order to avoid separation from the diffuser outer wall and to control the pressure gradient on the inner wall, suction was applied at the outer wall at the location indicated in Figure 2. | The testcase geometry is shown in Figure 2. It consists of an axisymmetric diffuser with an internally mounted cylinder along the centreline. In order to avoid separation from the diffuser outer wall and to control the pressure gradient on the inner wall, suction was applied at the outer wall at the location indicated in Figure 2. | ||
< | <center>[[Image:U3-03d32_files_image003.gif]]</center> | ||
<center>'''Figure 2 Schematic of flow geometry for CS0 Case'''</center> | |||
The following quantities have been measured: | The following quantities have been measured: | ||
| Line 54: | Line 47: | ||
The measurement section for the velocity profiles of the cylinder is 761.2 mm long and the inner cylinder has a diameter of 140 mm. The inlet velocity profiles are provided (velocity and turbulent stresses). The turbulent length (or time scale) has to be constructed from equilibrium assumptions. For the ω-equation based models, it is recommended to use | The measurement section for the velocity profiles of the cylinder is 761.2 mm long and the inner cylinder has a diameter of 140 mm. The inlet velocity profiles are provided (velocity and turbulent stresses). The turbulent length (or time scale) has to be constructed from equilibrium assumptions. For the ω-equation based models, it is recommended to use | ||
Related quantities like | <center><math>\omega_\mathrm{in}=\frac{1}{\sqrt{0.09}}\left|\frac{dU}{dy}\right|</math></center> | ||
Related quantities like <math>\varepsilon</math> can be computed from the known transformations | |||
<math>(\varepsilon=0.09k\omega)</math>. | |||
Pressure measurements have been conducted using 0.3 mm diameter static holes. The surface skin friction was measured with a laser-interferometer oil-flow technique. Additional skin friction measurements have been conducted using a surface Pitot tube. The estimates uncertainty of the wall shear stress measurements is within 10% of the measured value. | Pressure measurements have been conducted using 0.3 mm diameter static holes. The surface skin friction was measured with a laser-interferometer oil-flow technique. Additional skin friction measurements have been conducted using a surface Pitot tube. The estimates uncertainty of the wall shear stress measurements is within 10% of the measured value. | ||
The three velocity components have been measured with a laser Doppler velocimeter (only two components are relevant for the case CS0 | The three velocity components have been measured with a laser Doppler velocimeter (only two components are relevant for the case CS0 — however for the cases with a spinning inner cylinder 3D data are required). The estimated error in the velocity components is of the order of 1% of the freestream velocity. | ||
The turbulent stresses have also been obtained form the LDV measurements. Their accuracy is estimated to be within 10% of the local values for the normal stresses and 5% for the shear stresses. The experiments provide triple correlations, which are estimated to be within 4% of the local values. | The turbulent stresses have also been obtained form the LDV measurements. Their accuracy is estimated to be within 10% of the local values for the normal stresses and 5% for the shear stresses. The experiments provide triple correlations, which are estimated to be within 4% of the local values. | ||
| Line 68: | Line 64: | ||
The main obstacle in the simulation of this flow is the external boundary condition. As the outer cross-section is rectangular, but the testcase is computed axisymmetric, an artificial outer (slip) wall has to be provided. As it is difficult for some CFD codes to include the suction applied at the outer wall, the generic streamline also has to account for the effect of mass removal. The method chosen to close the domain is to integrate the experimental velocity ''U(x,r)'' profiles in the radial direction, ''r'', up to a height ''H(x)'' defined by a constant mass flow. | The main obstacle in the simulation of this flow is the external boundary condition. As the outer cross-section is rectangular, but the testcase is computed axisymmetric, an artificial outer (slip) wall has to be provided. As it is difficult for some CFD codes to include the suction applied at the outer wall, the generic streamline also has to account for the effect of mass removal. The method chosen to close the domain is to integrate the experimental velocity ''U(x,r)'' profiles in the radial direction, ''r'', up to a height ''H(x)'' defined by a constant mass flow. | ||
The mass flow is selected in a way that the outer streamline does not interfere with the boundary layer. It also has to be ensured that it is not too large in order to stay within the measured velocity profiles. The outer streamline ''H(x)'' used in the current simulations can be found [ | <center><math>\dot{m}=\int_0^{H(x)}\rho U(x,r)r\ dr=\mathrm{const.}</math></center> | ||
The mass flow is selected in a way that the outer streamline does not interfere with the boundary layer. It also has to be ensured that it is not too large in order to stay within the measured velocity profiles. The outer streamline ''H(x)'' used in the current simulations can be found | |||
[{{filepath:UFR3-03_streamline.dat}} here]. It has proven to be consistent with the rest of the experimental data. | |||
== CFD Methods == | == CFD Methods == | ||
| Line 101: | Line 100: | ||
has been performed. Figure 3 shows a comparison of the wall shear-stress distribution for the k-ε model for the three different grids. Note that the wall shear-stress is the most sensitive variable for this flow. | has been performed. Figure 3 shows a comparison of the wall shear-stress distribution for the k-ε model for the three different grids. Note that the wall shear-stress is the most sensitive variable for this flow. | ||
<center>[[Image:U3-03d32_files_image011.jpg]]</center> | <center>[[Image:U3-03d32_files_image011.jpg]]</center> | ||
<center>'''Figure 3 Grid resolutions study for CS0 case'''</center> | |||
The comparison shows that even the coarse grid seems sufficient when using a second order accurate CFD code. In order to ensure grid independence, the medium grid is recommended. Note however, that depending on the near wall treatment, specific restrictions apply for the near-wall resolution. For standard wall functions, the y<sup>+</sup> value of the first cell should typically not be smaller than a threshold value ([[Image:U3-03d32_files_image013.gif]] is a typical limit) defined by the model. This is a clear problem in terms of Best Practice Procedures, as it does not allow a systematic grid refinement. For most low-Re number turbulence models, an upper limit exists concerning the y<sup>+</sup> resolution ([[Image:U3-03d32_files_image015.gif]] is a typical limit). It must be ensured that the near wall grid spacing is consistent with the wall treatment of the code. Note however, that for both, wall functions and low-Re models, formulations have been developed which are insensitive to the near wall grid spacing (Esch et al. 2002). Depending on the wall treatment, a low-Reynolds number grid is recommended (y<sup>+</sup>~1). Note that some low-Re k-ε models require finer near wall meshes of the order of y<sup>+</sup>~0.1. | The comparison shows that even the coarse grid seems sufficient when using a second order accurate CFD code. In order to ensure grid independence, the medium grid is recommended. Note however, that depending on the near wall treatment, specific restrictions apply for the near-wall resolution. For standard wall functions, the y<sup>+</sup> value of the first cell should typically not be smaller than a threshold value ([[Image:U3-03d32_files_image013.gif]] is a typical limit) defined by the model. This is a clear problem in terms of Best Practice Procedures, as it does not allow a systematic grid refinement. For most low-Re number turbulence models, an upper limit exists concerning the y<sup>+</sup> resolution ([[Image:U3-03d32_files_image015.gif]] is a typical limit). It must be ensured that the near wall grid spacing is consistent with the wall treatment of the code. Note however, that for both, wall functions and low-Re models, formulations have been developed which are insensitive to the near wall grid spacing (Esch et al. 2002). Depending on the wall treatment, a low-Reynolds number grid is recommended (y<sup>+</sup>~1). Note that some low-Re k-ε models require finer near wall meshes of the order of y<sup>+</sup>~0.1. | ||
| Line 110: | Line 110: | ||
The boundary conditions are: | The boundary conditions are: | ||
* Inlet | * Inlet — specified velocity and turbulence quantities. | ||
* Outlet | * Outlet — subsonic outlet condition (pressure specified). | ||
* Outer wall | * Outer wall — inviscid wall (slip wall) | ||
* Cylinder | * Cylinder — No-slip wall (low-Re or wall functions). | ||
Note that the flow is at low Mach number (U~30m/s) and can be computed incompressible. The pressure can therefore be set arbitrarily. Following Best Practice Procedures, it has to be ensured that the solutions are converged to a level where the critical validation quantities do no longer change. The most sensitive quantity is the wall shear-stress distribution. | Note that the flow is at low Mach number (U~30m/s) and can be computed incompressible. The pressure can therefore be set arbitrarily. Following Best Practice Procedures, it has to be ensured that the solutions are converged to a level where the critical validation quantities do no longer change. The most sensitive quantity is the wall shear-stress distribution. | ||
| Line 128: | Line 128: | ||
{{UFR|front=UFR 3-03|description=UFR 3-03 Description|references=UFR 3-03 References|testcase=UFR 3-03 Test Case|evaluation=UFR 3-03 Evaluation|qualityreview=UFR 3-03 Quality Review|bestpractice=UFR 3-03 Best Practice Advice|relatedACs=UFR 3-03 Related ACs}} | {{UFR|front=UFR 3-03|description=UFR 3-03 Description|references=UFR 3-03 References|testcase=UFR 3-03 Test Case|evaluation=UFR 3-03 Evaluation|qualityreview=UFR 3-03 Quality Review|bestpractice=UFR 3-03 Best Practice Advice|relatedACs=UFR 3-03 Related ACs}} | ||
Latest revision as of 12:30, 12 February 2017
2D Boundary layers with pressure gradients (A)
Underlying Flow Regime 3-03 © copyright ERCOFTAC 2004
Test Case
Brief description of the study test case
The testcase geometry is shown in Figure 2. It consists of an axisymmetric diffuser with an internally mounted cylinder along the centreline. In order to avoid separation from the diffuser outer wall and to control the pressure gradient on the inner wall, suction was applied at the outer wall at the location indicated in Figure 2.
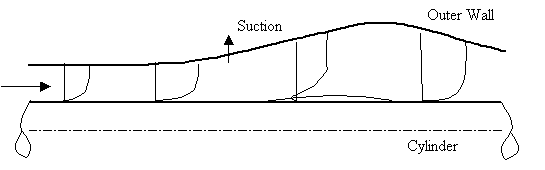
The following quantities have been measured:
- Wall pressure distribution.
- Wall shear stress distribution.
- Velocity profiles at 13 different stations.
- Turbulent stresses at 13 different stations.
- Triple-products at 13 different stations.
The Reynolds number based on the freestream velocity and the cylinder diameter is Re=2.8x105.
The testcase set-up has been used for additional studies with varying pressure gradients and with the additional complexity of one part of the cylinder spinning around the symmetry axis. These cases are also of high quality and recommended for validation of three-dimensional effects on turbulent flow predictions.
Test Case Experiments
The experiments have been carried out by Driver and Johnston (1990). The NASA TM contains all the experimental data including a diskette (and was kindly provided by D. Driver). The experiments have been carried out in the low-speed open circuit wind tunnel at NASA Ames.
The outer walls form a square testsection, which imposes a pressure gradient on the flow. Due to the elliptic nature of the pressure information, the pressure gradient on the cylinder is very close to being axisymmetric. Boundary layer suction was applied through slots on all four walls at a location 38 mm upstream of the location of wall divergence to avoid separation on the wind tunnel walls and in order to enhance the adverse pressure gradient. Approx. 10% of the mass flow was removed from the suction slots.
The measurement section for the velocity profiles of the cylinder is 761.2 mm long and the inner cylinder has a diameter of 140 mm. The inlet velocity profiles are provided (velocity and turbulent stresses). The turbulent length (or time scale) has to be constructed from equilibrium assumptions. For the ω-equation based models, it is recommended to use
Related quantities like can be computed from the known transformations
.
Pressure measurements have been conducted using 0.3 mm diameter static holes. The surface skin friction was measured with a laser-interferometer oil-flow technique. Additional skin friction measurements have been conducted using a surface Pitot tube. The estimates uncertainty of the wall shear stress measurements is within 10% of the measured value.
The three velocity components have been measured with a laser Doppler velocimeter (only two components are relevant for the case CS0 — however for the cases with a spinning inner cylinder 3D data are required). The estimated error in the velocity components is of the order of 1% of the freestream velocity.
The turbulent stresses have also been obtained form the LDV measurements. Their accuracy is estimated to be within 10% of the local values for the normal stresses and 5% for the shear stresses. The experiments provide triple correlations, which are estimated to be within 4% of the local values.
The quality of the flowfield has been carefully tested. The surface pressure taps indicated a variation of the pressure of less than 0.25% in circumferential direction. Circumferential skin friction measurements were within 4% of the upstream Cf.
The main obstacle in the simulation of this flow is the external boundary condition. As the outer cross-section is rectangular, but the testcase is computed axisymmetric, an artificial outer (slip) wall has to be provided. As it is difficult for some CFD codes to include the suction applied at the outer wall, the generic streamline also has to account for the effect of mass removal. The method chosen to close the domain is to integrate the experimental velocity U(x,r) profiles in the radial direction, r, up to a height H(x) defined by a constant mass flow.
The mass flow is selected in a way that the outer streamline does not interfere with the boundary layer. It also has to be ensured that it is not too large in order to stay within the measured velocity profiles. The outer streamline H(x) used in the current simulations can be found
here. It has proven to be consistent with the rest of the experimental data.
CFD Methods
The testcase was computed by a number of research groups, but has so far not been an official testcase in a validation workshop. The current validation studies refer to simulations carried out with the INS2D code of NASA Ames and to a second set of simulation using the code CFX-5 of ANSYS. Both codes are pressure-based, with the INS2D code using an artificial compressibility approach and the CFX-5 code a Rhie and Chow coupling.
A number of turbulence models have been used in the comparison. They include:
- Standard k-ε model (Jones and Launder 1972)
- RNG k-ε model (Yakhot et al. 1992)
- Standard k-ω model (Wilcox 1993)
- SST model (Menter 1993).
- Spalart-Allmaras one-equation model (Spalart and Allmaras 1994)
- Speziale-Sarkar-Gatski Reynolds Stress model (Speziale et al. 1991)
- Non-linear stress-strain models (compared by Hellsten and Laine 2000, Hsu et al. 2003)
A grid resolution study using three grids with:
- Coarse 61 x 31 (Grid 1)
- Medium 121 x 61 (Grid 2)
- Fine 241 x 121 (Grid 3)
has been performed. Figure 3 shows a comparison of the wall shear-stress distribution for the k-ε model for the three different grids. Note that the wall shear-stress is the most sensitive variable for this flow.
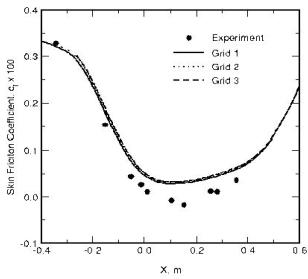
The comparison shows that even the coarse grid seems sufficient when using a second order accurate CFD code. In order to ensure grid independence, the medium grid is recommended. Note however, that depending on the near wall treatment, specific restrictions apply for the near-wall resolution. For standard wall functions, the y+ value of the first cell should typically not be smaller than a threshold value (![]() is a typical limit) defined by the model. This is a clear problem in terms of Best Practice Procedures, as it does not allow a systematic grid refinement. For most low-Re number turbulence models, an upper limit exists concerning the y+ resolution (
is a typical limit) defined by the model. This is a clear problem in terms of Best Practice Procedures, as it does not allow a systematic grid refinement. For most low-Re number turbulence models, an upper limit exists concerning the y+ resolution (![]() is a typical limit). It must be ensured that the near wall grid spacing is consistent with the wall treatment of the code. Note however, that for both, wall functions and low-Re models, formulations have been developed which are insensitive to the near wall grid spacing (Esch et al. 2002). Depending on the wall treatment, a low-Reynolds number grid is recommended (y+~1). Note that some low-Re k-ε models require finer near wall meshes of the order of y+~0.1.
is a typical limit). It must be ensured that the near wall grid spacing is consistent with the wall treatment of the code. Note however, that for both, wall functions and low-Re models, formulations have been developed which are insensitive to the near wall grid spacing (Esch et al. 2002). Depending on the wall treatment, a low-Reynolds number grid is recommended (y+~1). Note that some low-Re k-ε models require finer near wall meshes of the order of y+~0.1.
The boundary conditions are:
- Inlet — specified velocity and turbulence quantities.
- Outlet — subsonic outlet condition (pressure specified).
- Outer wall — inviscid wall (slip wall)
- Cylinder — No-slip wall (low-Re or wall functions).
Note that the flow is at low Mach number (U~30m/s) and can be computed incompressible. The pressure can therefore be set arbitrarily. Following Best Practice Procedures, it has to be ensured that the solutions are converged to a level where the critical validation quantities do no longer change. The most sensitive quantity is the wall shear-stress distribution.
© copyright ERCOFTAC 2004
Contributors: Florian Menter - AEA Technology



