UFR 2-04 Test Case: Difference between revisions
David.Fowler (talk | contribs) |
m (Dave.Ellacott moved page SilverP:UFR 2-04 Test Case to UFR 2-04 Test Case over redirect) |
||
| (26 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{UFR|front=UFR 2-04|description=UFR 2-04 Description|references=UFR 2-04 References|testcase=UFR 2-04 Test Case|evaluation=UFR 2-04 Evaluation|qualityreview=UFR 2-04 Quality Review|bestpractice=UFR 2-04 Best Practice Advice|relatedACs=UFR 2-04 Related ACs}} | {{UFR|front=UFR 2-04|description=UFR 2-04 Description|references=UFR 2-04 References|testcase=UFR 2-04 Test Case|evaluation=UFR 2-04 Evaluation|qualityreview=UFR 2-04 Quality Review|bestpractice=UFR 2-04 Best Practice Advice|relatedACs=UFR 2-04 Related ACs}} | ||
| Line 17: | Line 16: | ||
== Brief description of the study test case == | == Brief description of the study test case == | ||
The study test case concerns the measurements in a controlled diffusion compressor cascade. The main features of the cascade are included in '''Table 1'''. The blade coordinates, taken from Elazar and Shreeve (1990) are [ | The study test case concerns the measurements in a controlled diffusion compressor cascade. The main features of the cascade are included in [[SilverP:UFR_2-04_Description#table1|'''Table 1''']]. | ||
The blade coordinates, taken from Elazar and Shreeve (1990) are [[media:UFR2-04_blade.dat|blade.dat]]. | |||
The coordinate system used is illustrated in [[SilverP:UFR_2-04_References#fig3|'''Figure 3''']]. | |||
The flow is subsonic (inlet Mach number is about 0.25) and the Reynolds number of the flow is equal to 700,000. Measurements were carried out for three inlet air angles, from design to near stall conditions. | The flow is subsonic (inlet Mach number is about 0.25) and the Reynolds number of the flow is equal to 700,000. Measurements were carried out for three inlet air angles, from design to near stall conditions. | ||
The measurements were conducted at the subsonic cascade wind tunnel of the Naval Postgraduate School. The geometry of the test section is illustrated in '''Figure | The measurements were conducted at the subsonic cascade wind tunnel of the Naval Postgraduate School. The geometry of the test section is illustrated in [[SilverP:UFR_2-04_References#fig2|'''Figure 2''']]. | ||
Since the blade has been tested in cascade, apart from inlet, exit and stationary walls, all other boundaries are periodic. | |||
The test cascade consists of 20 blades that were cantilevered from a mounting plate attached to the fixed rear side-wall. The inlet air angle ([[Image:U2-04d32_files_image002.gif]]) was adjusted by means of the lower end-wall ([[Image:U2-04d32_files_image004.gif]]) and the upper end-wall ([[Image:U2-04d32_files_image006.gif]]) adjustment, as well as the use of inlet guide vanes (see '''Figure | The test cascade consists of 20 blades that were cantilevered from a mounting plate attached to the fixed rear side-wall. The inlet air angle ([[Image:U2-04d32_files_image002.gif]]) was adjusted by means of the lower end-wall ([[Image:U2-04d32_files_image004.gif]]) and the upper end-wall ([[Image:U2-04d32_files_image006.gif]]) adjustment, as well as the use of inlet guide vanes | ||
(see [[SilverP:UFR_2-04_References#fig2|'''Figure 2''']]). | |||
The test cascade moved horizontally as the end-walls were adjusted. | |||
A four-beam two-colour TS1 model 9100-7 LDV system with oil droplets as seeding was used for velocity measurements in the passage. The measurements were performed in passage formed by two consecutive | A four-beam two-colour TS1 model 9100-7 LDV system with oil droplets as seeding was used for velocity measurements in the passage. The measurements were performed in passage formed by two consecutive black–anodised blades. The resulting surface texture was better than 1.5micron. The measuring stations are illustrated in [[SilverP:UFR_2-04_References#fig3|'''Figure 3''']]. | ||
Verification of the air inlet angle was accomplished by means of a United Sensor Model DA-125 probe at 1.8 chords upstream. | Verification of the air inlet angle was accomplished by means of a United Sensor Model DA-125 probe at 1.8 chords upstream. | ||
| Line 35: | Line 39: | ||
== Test Case Experiments == | == Test Case Experiments == | ||
Inlet velocity was set to about 85m/s (yielding a Mach number of 0.25). The measured inlet turbulence intensity (as a result of the inlet guide vanes) was 1. | Inlet velocity was set to about 85m/s (yielding a Mach number of 0.25). The measured inlet turbulence intensity (as a result of the inlet guide vanes) was 1.4±0.2% in all cases. | ||
The Reynolds number was 700,000 in all cases. The stagnation quantities were 294 | The Reynolds number was 700,000 in all cases. The stagnation quantities were 294°K and 1.03atm. The exit static pressure was 1.0atm. | ||
Measurements were carried out for inlet air angles values of 40 | Measurements were carried out for inlet air angles values of 40° (design condition), 43.4° (about twice minimum losses condition) and 46v (near stall condition). | ||
The calculated maximum value of AVDR was 1.05. | The calculated maximum value of AVDR was 1.05. | ||
| Line 51: | Line 55: | ||
The quality of the experiments is high, as reported by Elazar and Shreeve (1990): | The quality of the experiments is high, as reported by Elazar and Shreeve (1990): | ||
* The uncertainty in measurement displacement from the blade surfaces is less than 0.05mm. | |||
* The uncertainty in pressure measurements is of the order of 12Pa. | |||
* The uncertainty in velocity measurements is of the order of 0.33% at 10m/s and 0.65% at 100m/s. | |||
* The discrepancy between the probe and LDV measurements at inlet was less than 0.1° for the angle. | |||
* The uniformity discrepancy at inlet is less ±1% for the velocity and 0.75° for the angle. | |||
* The periodicity of the flow downstream of the blades was confirmed. | |||
== | == TEST CASE EXP–1 == | ||
This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 40.0<sup>o</sup> (design conditions). Measurements of the static pressure coefficient along the blade. | This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 40.0<sup>o</sup> (design conditions). Measurements of the static pressure coefficient along the blade. | ||
[ | [[media:UFR2-04_exp1.dat|exp1.dat]] (ASCII file; headers: inlet flow angle: 40°, columns: chord-wise position, static pressure coefficient). | ||
== | == TEST CASE EXP–2 == | ||
This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 43.4 | This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 43.4°. Measurements of the static pressure coefficient along the blade. | ||
[ | [[media:UFR2-04_exp2.dat|exp2.dat]] (ASCII file; headers: inlet flow angle: 43.4°, columns: chord-wise position, static pressure coefficient). | ||
== | == TEST CASE EXP–3 == | ||
This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 46.0 | This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 46.0°. Measurements of the static pressure coefficient along the blade. | ||
[ | [[media:UFR2-04_exp3.dat|exp3.dat]] (ASCII file; headers: inlet flow angle: 46°, columns: chord-wise position, static pressure coefficient). | ||
== CFD Methods == | == CFD Methods == | ||
| Line 85: | Line 89: | ||
An overview of the methods used for computations in the study test case follows. Since the flow is low-speed, most of the methods used are elliptic. They are listed below in chronological order. | An overview of the methods used for computations in the study test case follows. Since the flow is low-speed, most of the methods used are elliptic. They are listed below in chronological order. | ||
* The fully elliptic solver of Kang et al. (1995) that is based on the SIMPLE algorithm. A single H-type grid comprising of 158x78 nodes in the stream-wise and span-wise direction respectively was used. Turbulence was modelled by either the low-Reynolds-number k-ε model (Launder and Sharma, 1974) or the Production Term Modification Model (PTMM, Schmidt and Patankar, 1991) that is based on the same model. The value of the first nodes off the solid boundaries [[Image:U2-04d32_files_image014.gif]] was 0.9~1.2. | |||
* The multi-block algorithm based on collocated grid arrangements of the pressure correction algorithm (Lien et al, 1996). An H-type grid, along with its four-block arrangement, and a four-block arrangement of H-O-type grids were alternatively used (see '''Figure 4''' for their layouts). Two linear low-Reynolds-number k–ε turbulence models (Lauder and Sharma, 1974 and Lien and Leschziner, 1993) and the non-linear variant of Craft et al. (1993) were employed in the computations. | |||
* The low-Reynolds-number k–ω model (Wilcox, 1994) enhanced with Menter’s (1992) modification in the turbulence production term were incorporated in the commercial FLUENT code and the third order accuracy QUICK scheme (Leonard, 1979) for the discretization of the convection terms was employed for computations (Tselepidakis, 1996). A single H-type grid consisting of 234x105 nodes was generated. 132 nodes discretized the blade surfaces. The value of the first nodes off the solid boundaries [[Image:U2-04d32_files_image014.gif]] was 0.1~2. | |||
* The implicit approximate factorisation, finite difference scheme (Biswas et al., 1997) combined with a higher order TVD scheme based in MUSCL approximation with Roe’s approximate solver. A C-type grid of 351x63 nodes was used. The low-Reynolds-number k–ε turbulence model developed by the authors was used (Biswas and Fukuyama, 1994). The minimum grid spacing in terms of [[Image:U2-04d32_files_image016.gif]] was 1.0. | |||
---- | ---- | ||
| Line 100: | Line 104: | ||
{{UFR|front=UFR 2-04|description=UFR 2-04 Description|references=UFR 2-04 References|testcase=UFR 2-04 Test Case|evaluation=UFR 2-04 Evaluation|qualityreview=UFR 2-04 Quality Review|bestpractice=UFR 2-04 Best Practice Advice|relatedACs=UFR 2-04 Related ACs}} | {{UFR|front=UFR 2-04|description=UFR 2-04 Description|references=UFR 2-04 References|testcase=UFR 2-04 Test Case|evaluation=UFR 2-04 Evaluation|qualityreview=UFR 2-04 Quality Review|bestpractice=UFR 2-04 Best Practice Advice|relatedACs=UFR 2-04 Related ACs}} | ||
Latest revision as of 19:39, 11 February 2017
Flow around (airfoils and) blades (subsonic)
Underlying Flow Regime 2-04 © copyright ERCOFTAC 2004
Test Case
Brief description of the study test case
The study test case concerns the measurements in a controlled diffusion compressor cascade. The main features of the cascade are included in Table 1. The blade coordinates, taken from Elazar and Shreeve (1990) are blade.dat. The coordinate system used is illustrated in Figure 3.
The flow is subsonic (inlet Mach number is about 0.25) and the Reynolds number of the flow is equal to 700,000. Measurements were carried out for three inlet air angles, from design to near stall conditions.
The measurements were conducted at the subsonic cascade wind tunnel of the Naval Postgraduate School. The geometry of the test section is illustrated in Figure 2. Since the blade has been tested in cascade, apart from inlet, exit and stationary walls, all other boundaries are periodic.
The test cascade consists of 20 blades that were cantilevered from a mounting plate attached to the fixed rear side-wall. The inlet air angle (![]() ) was adjusted by means of the lower end-wall (
) was adjusted by means of the lower end-wall (![]() ) and the upper end-wall (
) and the upper end-wall (![]() ) adjustment, as well as the use of inlet guide vanes
(see Figure 2).
The test cascade moved horizontally as the end-walls were adjusted.
) adjustment, as well as the use of inlet guide vanes
(see Figure 2).
The test cascade moved horizontally as the end-walls were adjusted.
A four-beam two-colour TS1 model 9100-7 LDV system with oil droplets as seeding was used for velocity measurements in the passage. The measurements were performed in passage formed by two consecutive black–anodised blades. The resulting surface texture was better than 1.5micron. The measuring stations are illustrated in Figure 3.
Verification of the air inlet angle was accomplished by means of a United Sensor Model DA-125 probe at 1.8 chords upstream.
The velocity measurements were verified by hot-wire measurements at several measuring stations.
Forty pressure taps were used to obtain pressure measurements on the blade surfaces.
Test Case Experiments
Inlet velocity was set to about 85m/s (yielding a Mach number of 0.25). The measured inlet turbulence intensity (as a result of the inlet guide vanes) was 1.4±0.2% in all cases.
The Reynolds number was 700,000 in all cases. The stagnation quantities were 294°K and 1.03atm. The exit static pressure was 1.0atm.
Measurements were carried out for inlet air angles values of 40° (design condition), 43.4° (about twice minimum losses condition) and 46v (near stall condition).
The calculated maximum value of AVDR was 1.05.
Measurements of the normal and the parallel to the blade surface velocity components, as well as of the turbulence intensity were recorded.
Measurements of pressure on the blade surfaces were recorded.
Boundary layer quantities have been calculated by post-processing the measurements.
The quality of the experiments is high, as reported by Elazar and Shreeve (1990):
- The uncertainty in measurement displacement from the blade surfaces is less than 0.05mm.
- The uncertainty in pressure measurements is of the order of 12Pa.
- The uncertainty in velocity measurements is of the order of 0.33% at 10m/s and 0.65% at 100m/s.
- The discrepancy between the probe and LDV measurements at inlet was less than 0.1° for the angle.
- The uniformity discrepancy at inlet is less ±1% for the velocity and 0.75° for the angle.
- The periodicity of the flow downstream of the blades was confirmed.
TEST CASE EXP–1
This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 40.0o (design conditions). Measurements of the static pressure coefficient along the blade.
exp1.dat (ASCII file; headers: inlet flow angle: 40°, columns: chord-wise position, static pressure coefficient).
TEST CASE EXP–2
This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 43.4°. Measurements of the static pressure coefficient along the blade.
exp2.dat (ASCII file; headers: inlet flow angle: 43.4°, columns: chord-wise position, static pressure coefficient).
TEST CASE EXP–3
This test case corresponds to the flow to the text cascade for an inlet flow angle angle of 46.0°. Measurements of the static pressure coefficient along the blade.
exp3.dat (ASCII file; headers: inlet flow angle: 46°, columns: chord-wise position, static pressure coefficient).
CFD Methods
An overview of the methods used for computations in the study test case follows. Since the flow is low-speed, most of the methods used are elliptic. They are listed below in chronological order.
- The fully elliptic solver of Kang et al. (1995) that is based on the SIMPLE algorithm. A single H-type grid comprising of 158x78 nodes in the stream-wise and span-wise direction respectively was used. Turbulence was modelled by either the low-Reynolds-number k-ε model (Launder and Sharma, 1974) or the Production Term Modification Model (PTMM, Schmidt and Patankar, 1991) that is based on the same model. The value of the first nodes off the solid boundaries
 was 0.9~1.2.
was 0.9~1.2.
- The multi-block algorithm based on collocated grid arrangements of the pressure correction algorithm (Lien et al, 1996). An H-type grid, along with its four-block arrangement, and a four-block arrangement of H-O-type grids were alternatively used (see Figure 4 for their layouts). Two linear low-Reynolds-number k–ε turbulence models (Lauder and Sharma, 1974 and Lien and Leschziner, 1993) and the non-linear variant of Craft et al. (1993) were employed in the computations.
- The low-Reynolds-number k–ω model (Wilcox, 1994) enhanced with Menter’s (1992) modification in the turbulence production term were incorporated in the commercial FLUENT code and the third order accuracy QUICK scheme (Leonard, 1979) for the discretization of the convection terms was employed for computations (Tselepidakis, 1996). A single H-type grid consisting of 234x105 nodes was generated. 132 nodes discretized the blade surfaces. The value of the first nodes off the solid boundaries
 was 0.1~2.
was 0.1~2.
- The implicit approximate factorisation, finite difference scheme (Biswas et al., 1997) combined with a higher order TVD scheme based in MUSCL approximation with Roe’s approximate solver. A C-type grid of 351x63 nodes was used. The low-Reynolds-number k–ε turbulence model developed by the authors was used (Biswas and Fukuyama, 1994). The minimum grid spacing in terms of
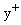 was 1.0.
was 1.0.
Contributors: E. S. Politis - NTUA