UFR 4-09 Description
Confined buoyant plume
Underlying Flow Regime 4-09 © copyright ERCOFTAC 2004
Description
Introduction
Buoyant plumes within confined spaces are an important generic component of air flows in buildings. Such plumes occur whenever there is a heat source at low level — for example, a person, equipment or sun-patch. The heated air rises from the thermal source to produce a plume of warm air that rises within the space. On reaching ceiling level, the buoyant air will spread out laterally to form a warm layer. The principal of displacement ventilation is to maintain the level of this warm layer above the level of occupation. This enables comfort conditions to be maintained in the occupied zone without the need to condition the whole of the space.
The dynamics of thermal plumes play a central role in displacement ventilation, through impact on:
- temperature and pollutant distributions
- ventilation supply air temperature and volume flow rate requirements
- buoyancy-driven natural ventilation rates
In order to optimise the performance of displacement systems it is desirable to model the buoyancy-driven air flows associated with thermal plumes, typically along-side the other environmental factors affecting the thermal dynamics of the space, such as solar gain to room surfaces, distribution of occupants and heat sources, and conduction of heat through room fabric.
This UFR focuses on the contribution of the plume dynamics to these flows. Turbulent plumes are a challenging flow to model using CFD. It is fundamental, therefore, to ensure that this basic "building block" of buoyancy-driven flow is modelled correctly. The situation considered here is a simple and robust one, consisting of a single plume in a box with low-level supply and high-level extract. The situation is an attractive one for the UFR as it presents a steady-state flow for which recent CFD work has been carried out and successfully compared to both experiment and theory.
This UFR is also of particular relevance to UFR1-03 Buoyant plumes.
Review of UFR studies and choice of test case
2.1 Confined plume flows — simple cases
The classical flow associated with a plume in an enclosed space is the ‘filling box’ (Turner 1973). Consider a single point-source of buoyancy (e.g. heat source), with constant strength in time, situated centrally in a rectangular space with perfectly insulating (adiabatic) boundaries. A plume forms above the buoyancy source and rises to reach the ceiling where it spreads out laterally. This creates a layer of buoyant fluid at the ceiling. The depth of this layer increases with time as further buoyant fluid is supplied from the plume (Figure 1). In fact, the buoyant layer will be stratified in density. A fundamental property of plumes is that they entrain ambient fluid from the surroundings due to the turbulence created at the plume edge (where there is strong shear). This means that as a fluid parcel rises within the plume, it will lose buoyancy due to mixing with the surrounding air. The amount of buoyancy lost depends on the distance between the buoyancy source and the base of the warm layer. As the layer deepens, this distance decreases and so fluid parcels reaching the warm layer have lost less buoyancy and continue to rise. In this way the layer becomes stably stratified. Eventually, the base of the stratified region will reach the floor. Thereafter the stratification weakens with time, until such point as the whole space is at the temperature of the thermal source.
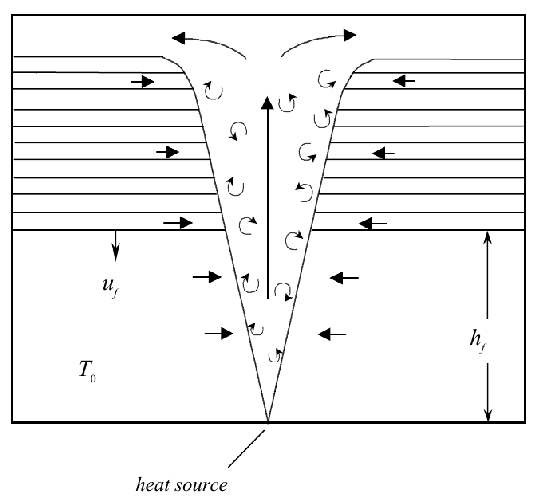
Figure 1. Schematic of the ‘filling box’ flow. Buoyant fluid rises vertically in the plume then collects in the upper part of the space forming a stratified layer (the horizontal lines represent constant density surfaces in the stratified layer). The leading ‘front’ of the stratified region, at height hf, descends at speed uf , until reaching the floor after some time. The plume entrains fluid from both the homogeneous and stratified regions. In the latter region, the entrainment produces a horizontal flow along constant density surfaces towards the plume. After the front has reached the floor, the stratification weakens and eventually the whole space becomes well mixed. Originals of all the figures in this UFR are in UFR4-09_Figures.pdf
In a displacement ventilation system, it is desirable to maintain the base of the warm layer above the occupied zone. This may be possible if cooler air is supplied at low level and warmer air allowed to leave at high level (Figure 2). This flow has been described as the ‘emptying-filling box’ (Linden et al 1990). In the naturally ventilated case in which the air flow is driven through the openings solely by the buoyancy of the room air, then the basic components of the flow are:
- the plume — which carries air vertically through the space
- the hydrostatic pressure difference between the interior of the space and the external surroundings due to the lower density of the warmer interior air (the so-called ‘stack effect’)
- the nature of the openings through which air enters and leaves the space — their size, position, and respective discharge characteristics

Figure 2. Definition sketch and schematic of the ‘emptying-filling box’ flow. Air at temperature T0 enters the space through the bottom opening, of area ab. The plume carries buoyant fluid from the plume source together with entrained ambient fluid into the upper layer. On reaching the upper layer the plume dissipates and maintains well-mixed conditions in the upper the layer at temperature T0+ΔT. The interface between the two layers, at height h is quite sharp. Warm air in the upper layer leaves through the top opening, of area at. Originals of all the figures in this UFR are in UFR4-09_Figures.pdf
Linden et al. (1990) and Hunt & Linden (2001) have studied these flow components theoretically and in small-scale laboratory experiments using saline plumes in fresh water as an analogy for warm plumes in air — the so-called ‘salt bath’ method. The theoretical models developed were found to be in good agreement with experiment. Key findings have been:
For a single plume:
- A steady-state is reached, in which there is a two layer stratification consisting of a well-mixed upper buoyant layer overlying a lower layer which, outside the plume, is also well-mixed. The two layers are separated by a sharp density interface. The lower layer is at the density of the ambient fluid supplied to the room by the low level openings. The upper layer is at the density of the fluid within the plume where the plume meets the interface. The plume dissipates on reaching the upper layer, creating a circulation that maintains well-mixed conditions in the upper layer.
- A central aspect of the dynamics is the volume of fluid entrained into the plume over its vertical extent — the distance between the buoyancy source and the interface. The steady state is reached when this volume entrainment equals the total volume flow rate through the space.
- The total flow rate through the room is set by the stack effect through the combination of i) the density of the upper layer relative to ambient fluid and ii) the depth of the upper layer. The first factor is set by the plume dynamics whereas the second is set by the required net flow rate — this means that the ventilation rate and interface height become coupled to the dynamics of the plume. It may be shown that the nature of this coupling for ideal plumes means that the interface height is independent of the strength of the buoyancy source and depends only on the effective area of the openings A* (defined in Section 3).
For multiple plumes or distributed heat sources:
- The dynamics are similar to those of the single-plume case, but the stratification becomes more complex. For a moderate number of sources there will be a number of ‘warm’ layers, each associated with plumes of different strength. For a large number of plumes the density interfaces will break down and the stratification become continuous. (Cooper & Linden 1996; Linden & Copper 1996).
Although a generic simple case, and one fundamental to building ventilation, only two CFD studies appear to have been made of the emptying-filling box flow.
The first is the work of Cook & Lomas (1997, 1998) and Cook (1998). They considered line-source and point-source thermal plumes in a full size enclosure with air as the working fluid. The aim of the work was to make comparisons with the theoretical and experimental work of Linden et al (1990). Conditions were therefore chosen to mirror those in the salt bath experiments, namely adiabatic boundaries and no radiative heat transfer. Simulations were made using two different two-equation eddy viscosity turbulence models. The first was the ‘standard’ k – ε model, as described by Launder & Spalding (1974), and the second the RNG k – ε model of Yakhot et al. (1992). The RNG model is similar to the ‘standard’ model but has different values for the numerical constants (derived using renormalisation group theory) and includes an additional term in the ε – equation, representing dissipation by mean flow distortion. The simulations made using both turbulence models gave good qualitative agreement, and reasonable quantitative agreement with the theoretical and experimental results of Linden et al.
The second study is the work of Howell & Potts (2002). The aim of their study was to address the effects of radiative heat transfer which are not included in the salt-bath experiments. Rather than use this methodology, therefore, they carried out experiments on a thermal plume in air in a full-scale environmental chamber. The results were qualitatively very different the results of the salt-bath experiments. While a clear 2-layer stratification structure existed, there was significant stratification within each layer. The form of the density profiles and the level of the boundary between the two layers was found to be insensitive to the effective opening area A*. The baseline temperature for the profiles was however found to depend on A*.
Howell & Potts (2002) carried out CFD modelling of their experiments using eddy viscosity k – ε turbulence models and a radiative heat transfer model that enables absorption of radiation by water vapour. Although reasonable agreement was obtained with the experimental results, quantitative agreement was only found when the radiative model was included and allowance made for absorption of radiation by air moisture. This result led these authors to conclude that radiative heat transfer and air moisture content were fundamental aspects of the dynamics and the reason for the difference with the salt-bath experiments. However, this conclusion does not appear to be correct, since the CFD simulations made without the radiation model showed dynamics markedly different from those of the salt-bath experiments. These observations point to a more fundamental difference between the dynamics of the two cases, although at this stage it is unclear what the source of these differences is.
2.2 Displacement ventilation
Displacement ventilation flows in real buildings are typically more complex than the simple emptying–filling box flows described above. In addition to both radiative effects and multiple sources of buoyancy being present, the system may also make use of static cooling and mixing devices that extend the range of cooling loads the system can provide. Such features include swirl inlets, which increase the mixing of incoming air to allow lower temperature air to be supplied directly to the space, and chilled beams, which provide direct cooling to the upper part of the space through convective heat exchange at the beam surface. Typically in such systems the ventilation rate is mechanically controlled.
Both physical modelling (reduced-scale and full-scale) and CFD modelling of mechanical displacement systems have been carried out. Physical models generally show a 2-layer stratification structure, with continuous stratification in the lower layer and more well-mixed conditions above (e.g. Woolf 1994, 1995; Abbas 1999; Chen & Srebric 2000). CFD simulations have been reported by Woolf (1995) and Chen & Srebric (2000). Woolf (1994, 1995) considered the case of a single plume with mechanically-driven floor level supply through swirl inlet diffusers. Reasonable agreement was achieved with a high resolution k – ε model. Chen & Srebric (2000) report both RANS and LES simulations of mechanically-driven displacement ventilation in a office space with a variety of heat sources, a tall wall inlet and ceiling outlet resulting in weakly stratified conditions. Some agreement between CFD and experiment was found, but this was described as being "acceptable rather than excellent". While the LES results had better agreement than the RANS results for the lower part of the space, the reverse was true for the upper part. No firm conclusions on the accuracy of different methods could be drawn from this study therefore.
2.3 Choice of UFR
The emptying-filling box flow described in §2.1 has been chosen for the UFR, specifically the work of Linden et al., Hunt & Linden and Cook & Lomas. The reasons for this are as follows:
- The situation presents a simple and robust flow with well defined governing parameters
- CFD modelling of the situation has been carried out (Cook & Lomas 1997, 1998; Cook 1998) and compared successfully with both experiment and theory.
- The flow is governed by turbulent plume entrainment dynamics and so provides a stringent test of both buoyancy and turbulence model implementation
- The case presents a useful platform on which to build additional complexity, such as multiple heat sources, heat conducting boundaries, radiation modelling, and wind-driven natural ventilation (e.g. see Cook, Ji & Hunt 2003).
While the study of Howell & Potts considers a similar case and is of high interest to the UFR, we do not propose to include this study. This is in view of the apparent inconsistencies between this and other published work which we believe require resolution before guidance can be given based on this work. We also do not intend to include the CFD studies of displacement ventilation flows described in §2.2. This is because these are deemed to be case-specific and over-complex for the purposes of the UFR.
© copyright ERCOFTAC 2004
Contributors: Jake Hacker - Arup