UFR 4-18 Evaluation: Difference between revisions
| Line 95: | Line 95: | ||
Note that the experimental results have an error of +/- 12%, +/-11.4%, and +/-10.5% for the 3 000, 10 000, and 30 000 Reynolds numbers, respectively, in the endwall regions adjacent to the pins and +/- 9% away from the pin. | Note that the experimental results have an error of +/- 12%, +/-11.4%, and +/-10.5% for the 3 000, 10 000, and 30 000 Reynolds numbers, respectively, in the endwall regions adjacent to the pins and +/- 9% away from the pin. | ||
One can see that the two models using a first moment closure (φ-model and kω-SST) are too far from the experimental results, except the φ-model at <math>Re_D=30000</math> but which, as it will be shown later, exhibits a wrong physics. LES and EB-RSM exhibits very satisfactory values in the error interval. The superiority of these two models will be discussed later while dealing with the local normalized Nusselt number on the bottom wall. Ames and Dvorak (2006a) used standard, Realizable and RNG k-&epsilon. They showed a substantial underestimation of the averaged Nusselt number when the pins were heated. | One can see that the two models using a first moment closure (φ-model and kω-SST) are too far from the experimental results, except the φ-model at <math>Re_D=30000</math> but which, as it will be shown later, exhibits a wrong physics. LES and EB-RSM exhibits very satisfactory values in the error interval. The superiority of these two models will be discussed later while dealing with the local normalized Nusselt number on the bottom wall. Ames and Dvorak (2006a) used standard, Realizable and RNG k-ε. They showed a substantial underestimation of the averaged Nusselt number when the pins were heated. | ||
Delibra et al. (2009) used the URANS ζ-f model (very close to the φ-model utilized in the present work) at the 10000 and 30000 Reynolds numbers. They obtained averaged Nusselt numbers of 46.2 and 122.3, respectively. These values are higher than those obtained in the present work and closer to experimental values.The temperature was imposed at the wall in Delibra et al. (2009). Imposing the temperature at the wall in the present work with the φ-model led to averaged Nusselt numbers of 41 and 100, respectively. This shows that imposing the temperature gives higher Nusselt numbers that by imposing the heat flux with this model. The effect of the temperature boundary condition has also been tested with the LES at <math>Re_D=10000</math> and the EB-RSM at <math>Re_D=30000</math>. The averaged Nusselt numbers were equal to 46 and 115.2, respectively. No clear conclusion can be drawn for these two models which give a more realistic physics than the models using a first moment closure concerning the effect of imposing the temperature instead of the heat flux at the bottom wall. However, one can state that there is a difference between the two methods. | Delibra et al. (2009) used the URANS ζ-f model (very close to the φ-model utilized in the present work) at the 10000 and 30000 Reynolds numbers. They obtained averaged Nusselt numbers of 46.2 and 122.3, respectively. These values are higher than those obtained in the present work and closer to experimental values.The temperature was imposed at the wall in Delibra et al. (2009). Imposing the temperature at the wall in the present work with the φ-model led to averaged Nusselt numbers of 41 and 100, respectively. This shows that imposing the temperature gives higher Nusselt numbers that by imposing the heat flux with this model. The effect of the temperature boundary condition has also been tested with the LES at <math>Re_D=10000</math> and the EB-RSM at <math>Re_D=30000</math>. The averaged Nusselt numbers were equal to 46 and 115.2, respectively. No clear conclusion can be drawn for these two models which give a more realistic physics than the models using a first moment closure concerning the effect of imposing the temperature instead of the heat flux at the bottom wall. However, one can state that there is a difference between the two methods. | ||
Delibra et al. (2008) also reported LES computations. The one used for <math>Re_D=30000</math> was too coarse with a short time integration and will not be considered here. LES at <math>Re_D=10000</math> gave an average Nusselt number equal to 44.3 which is lower than the one obtained in the present work even with a fixed temperature at the wall. The error compared to the experimental value is equal to 18% which is too high. This discrepancy can be attributed to two factors: | Delibra et al. (2008) also reported LES computations. The one used for <math>Re_D=30000</math> was too coarse with a short time integration and will not be considered here. LES at <math>Re_D=10000</math> gave an average Nusselt number equal to 44.3 which is lower than the one obtained in the present work even with a fixed temperature at the wall. The error compared to the experimental value is equal to 18% which is too high. This discrepancy can be attributed to two factors: | ||
Revision as of 21:22, 7 October 2015
Flow and heat transfer in a pin-fin array
Confined Flows
Underlying Flow Regime 4-18
Evaluation
Comparison of CFD Calculations with Experiments
Global comparisons
Pressure loss coefficient
The following table gives the numerical values of the presure loss coefficient in Ames et al. experiment as well as those obtained in the main computations. Note that the experimental data shown here have been sent by the authors of the experiment and are different from the one found in Ames et al. (2005).
Figure 1 shows these values and compare them to existing correlations from the literature (note that Ames et al. experimental values are very close to Metzger et al. correlation):
- Metzger et al. (1982) :
for , Failed to parse (syntax error): {\displaystyle f = 0.317 {Re_D}^{−0.132} } , for , Failed to parse (syntax error): {\displaystyle f = 1.76 {Re_D}^{−0.318}}
- Jacob (1938) :
Table 1 compares the comptations to the experiment and gives the relative errors. Large Eddy Simulation shows a very good agreement with the correlations and Ames et al. experimental results. The relative error is equal to 1% end 3% for the two Reynolds numbers, respectively, for both computed Reynolds numbers. The EB-RSM shows a very satisfactory pressure loss coefficient at (1% error) but the result is worse at (10% error). The kω-SST shows globally good results (7% and 6% errors) and the φ-model poorer results with an error of 17% and 12% for the two Reynolds numbers, respectively.
Wall resolved LES is then a good candidate to obtain satisfactory pressure loss coefficients in the present configuration. The EB-RSM gives very good results at the lowest Reynolds number but a substantial error is observed at . Although the kω-SST exhibits pretty good results, the physics of the present flow is not well captured as it will be shown later and one can't rely on this model. The φ-model gives the worse results and is not reliable.
| Ames et al. | LES3000 | Ames et al. | LES10000 | EBRSM10000 | PHI10000 | kwSST10000 | Ames et al. | EBRSM30000 | PHI30000 | kwSST30000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | 0.111 | 0.1076 | 0.095 | 0.0939 | 0.0963 | 0.0789 | 0.0883 | 0.07 | 0.0771 | 0.0615 | 0.0744 |
| Error (%) | - | 3 | - | 1 | 1 | 17 | 7 | - | 10 | 12 | 6 |
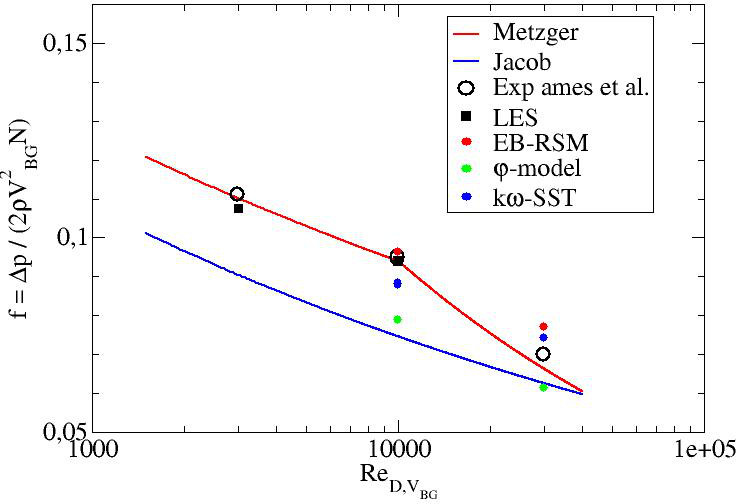
Figure 1: Pressure loss coefficient
Average Nusselt Number
The following table gives the numerical values of the average Nusselt numbers on the bottom wall in Ames et al. experiment as well as those obtained in the main computations.
Figure 2 shows these values and compare them to existing correlations from the literature:
- Metzger et al. (1982) :
- Van Fossen (1982) :
Note that the experimental results have an error of +/- 12%, +/-11.4%, and +/-10.5% for the 3 000, 10 000, and 30 000 Reynolds numbers, respectively, in the endwall regions adjacent to the pins and +/- 9% away from the pin.
One can see that the two models using a first moment closure (φ-model and kω-SST) are too far from the experimental results, except the φ-model at but which, as it will be shown later, exhibits a wrong physics. LES and EB-RSM exhibits very satisfactory values in the error interval. The superiority of these two models will be discussed later while dealing with the local normalized Nusselt number on the bottom wall. Ames and Dvorak (2006a) used standard, Realizable and RNG k-ε. They showed a substantial underestimation of the averaged Nusselt number when the pins were heated. Delibra et al. (2009) used the URANS ζ-f model (very close to the φ-model utilized in the present work) at the 10000 and 30000 Reynolds numbers. They obtained averaged Nusselt numbers of 46.2 and 122.3, respectively. These values are higher than those obtained in the present work and closer to experimental values.The temperature was imposed at the wall in Delibra et al. (2009). Imposing the temperature at the wall in the present work with the φ-model led to averaged Nusselt numbers of 41 and 100, respectively. This shows that imposing the temperature gives higher Nusselt numbers that by imposing the heat flux with this model. The effect of the temperature boundary condition has also been tested with the LES at and the EB-RSM at . The averaged Nusselt numbers were equal to 46 and 115.2, respectively. No clear conclusion can be drawn for these two models which give a more realistic physics than the models using a first moment closure concerning the effect of imposing the temperature instead of the heat flux at the bottom wall. However, one can state that there is a difference between the two methods. Delibra et al. (2008) also reported LES computations. The one used for was too coarse with a short time integration and will not be considered here. LES at gave an average Nusselt number equal to 44.3 which is lower than the one obtained in the present work even with a fixed temperature at the wall. The error compared to the experimental value is equal to 18% which is too high. This discrepancy can be attributed to two factors:
- the mesh was probably still too coarse, not in the wall normal directions but in the stream-wise and span-wise ones (the mesh in the present study contains 76 million cells and their mesh contained 5.5 million cells),
- the boundary condition using an imposed temperature is less representative of the experiment.
Finally, Delibra et al. (2010) tried to use a hybrid RANS/LES approach to overcome the understimation of the Nusselt number but the results where close to the ones obtained with the URANS approach based on the ζ-f model.
| Ames et al. 3000 | LES3000 | Ames et al. 10000 | LES10000 | EBRSM10000 | PHI10000 | kwSST10000 | Ames et al. 30000 | EBRSM30000 | PHI30000 | kwSST30000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | 22.1 | 21.6 | 54.1 | 48.6 | 48.1 | 37.6 | 33.1 | 111.5 | 114.8 | 93.3 | 72 |
| Error (%) | - | 2 | - | 10 | 11 | 30 | 39 | - | 3 | 16 | 35 |
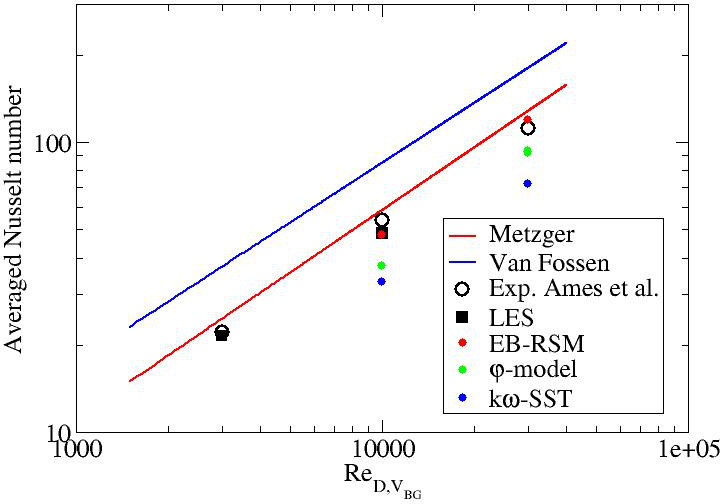
Figure 2: Averaged Nusselt number on the bottom wall
Local comparisons
Mean pressure coefficient
Figures ?? to ?? give the profiles of the pressure coefficient along the midline of pins 1, 2, 3 and 5 for the three Reynolds numbers.
Note that the experimental results have an uncertainty equal to +/-0.075 at and to +/-0.025 at and .
LES results are in relatively good agreement with the experimental data. EB-RSM exhibits decent results as well. The two first moment closure models show poor results in particular the φ-model. The prediction of the coefficient may be related to the wake prediction downstream the pins.
Figures ?? and ?? display the mean stream-wise velocity field in the midplane (Z=H). The wakes donwstream the cylinders are similar in LES and EB-RSM. The wakes are shorter downstream the cylinders from row 4. The longer wakes are obtained for rows 1 and 2, then then lengths decreases. This is not observed at all for the φ-model and the kω-SST models. One can state at this stage that first moment closures are not able the predict the present flow. One will still plot the values obtained with these two models but without analysing deeply the results.
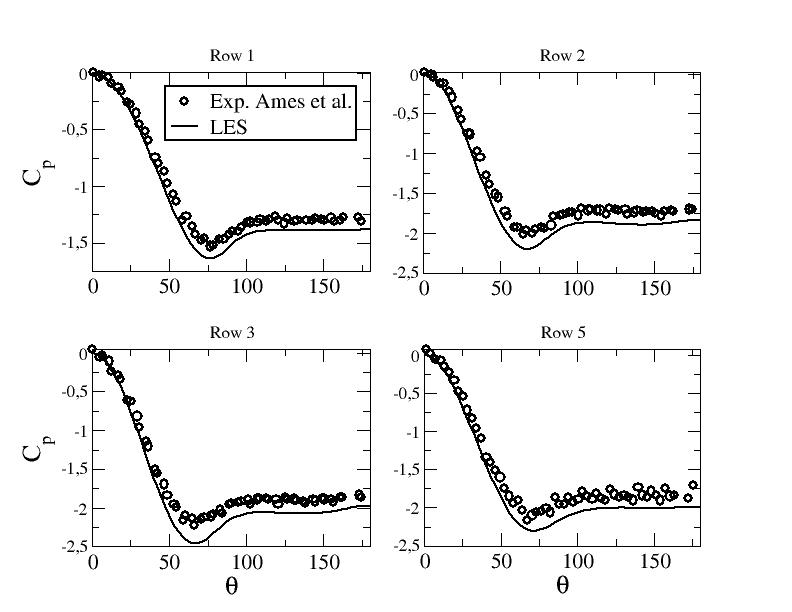
Figure ??: Pressure coefficient along the midline of the pins - LES at

Figure ??: Pressure coefficient along the midline of the pins - LES and URANS computations at

Figure ??: Pressure coefficient along the midline of the pins - URANS computations at

Figure ??: Mean stream-wise velocity in the midplane z=H at

Figure ??: Mean stream-wise velocity in the midplane z=H at
Mean velocity profiles
Figures ?? show the mean axial velocity component along line B for the different computations. The first moment closure exhibits a dramatic deficit of the mean axial velocity. On the other hand, LES and EB-RSM perform well compared to the experimental data with a slight overestimation of the mean stream-wise velocity peaks close to the walls in several locations, in particular departin from row 4. Note that the convergence study shown in "Test Case Studies" section proved that the needed refinement to obtain a convergent solution around pin 2 is very important (with the first two levels of refinement, a deficit in the central velocity was observed). Figure ?? shows the means axial velocity component along line A1 for the highest Reynolds number. One can see again that the linear eddy viscosity models are unable to predict the present flow. The results with the EB-RSM are much closer to experimental data. However, the flow redistribution doesn't seem to be similar to the one obtained experimentally. This may come from the periodic boundary conditions used in the present work v.s. confined conditions in the experiment.
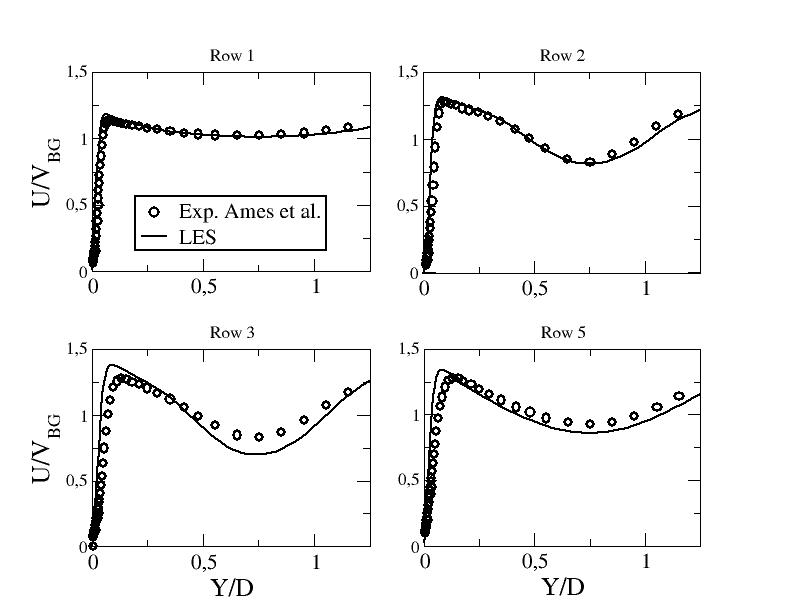
Figure ??: Mean stream-wse velocity component along line B - LES at

Figure ??: Mean stream-wse velocity component along line B - LES and URANS computations at
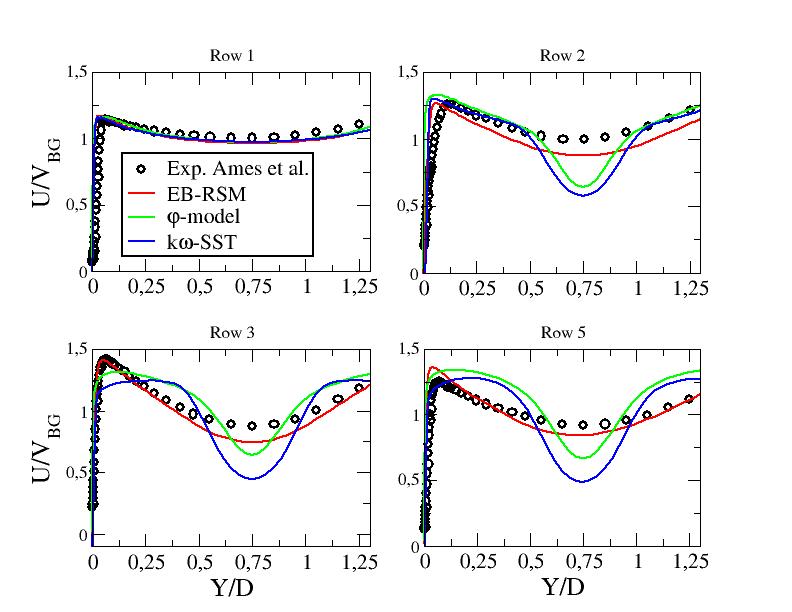
Figure ??: Mean stream-wse velocity component along line B - URANS computations at

Figure ??: Mean stream-wse velocity component along line A1 - URANS computations at
R.m.s. velocity profiles
Figures ?? and figure ?? show the r.m.s. value of the stream-wise velocity along line B and line A1, respectively. The first moment closure models are very far from the experimental measurements. On the other hand, LES and EB-RSM perform well compared to the experimental data with a certain superiority of LES. One can notice an overestimation of the r.m.s. value of the stream-wise velocity component with the EB-RSM in the central part of row 5 (along both lines B and A1).
Figures ?? and figure give the detailed profiles of the resolved and modelled stresses for the two Reynolds numbers at which the test case is performed with URANS approaches along lines B and A1, respectively. One assumes here that the total Reynolds stress is given by the sum of the modelled part and the resolved one: , where is the velocity fluctuation (resolved part) and the time averaged value of the modelled Reynolds stress . First, the EB-RSM doesn't degenrates to a Large Eddy Simulation. The modelled part does't vanish and enhances the total level of turbulence. The linear eddy viscosity models fail naturally to predict the normal stresses. Figures ?? give the modelled and resolved stresses in the mid-plane in order to have a better overview of the behavior of this quantity (the whole computational domain is not represented to enhance clarity). The kω-SST model is clearly steady upstream of row 5 for both Reynolds numbers. The φ-model shows some unsteadiness departing from row 3 at Re=10000 but is totally steady at $Re=30000$. Note that at this Reynolds number, the φ-model exhibited unsteadiness everywhere with a coarser mesh. This is an exemple of a computation which might exhibit unsteadiness at relatively coarse meshes and gives a steady solution after important refinement (see Fadai-Ghotbi et al. (2008)).

Figure ??: R.m.s. of the stream-wise velocity component along line B - LES at

Figure ??: R.m.s. of the stream-wise velocity component along line B - LES and URANS computations at

Figure ??: R.m.s. of the stream-wise velocity component along line B - URANS computations at

Figure ??: R.m.s. of the stream-wise velocity component along line A1 - URANS computations at

Figure ??: Resolved and modelled contributions to the r.m.s. of the stream-wise velocity component along line B - URANS computations at

Figure ??: Resolved and modelled contributions to the r.m.s. of the stream-wise velocity component along line B - URANS computations at

Figure ??: Resolved and modelled contributions to the r.m.s. of the stream-wise velocity component along line A1 - URANS computations at

Figure ??: Resolved and modelled contributions to the r.m.s. of the stream-wise velocity component in the midplane - LES and URANS computations at

Figure ??: Resolved and modelled contributions to the r.m.s. of the stream-wise velocity component in the midplane - URANS computations at
Strouhal numbers
The Strouhal numbers which will be given in the folowing are based on the gap velocity and the cynlinders diameter D: . The folowing table summarizes the Strouhal numbers given by Ames et al. (2006a) and Delibra et al. (2009) for the first pin at different Reynolds numbers. Ames et al. (2006a) show time histories for row 2 at the three Reynolds numbers but they don't estimated Strouhal numbers.
| Reynolds number | Ames et al. (2006a) | Delibra et al. (2009)/LES | Delibra et al. (2009)/URANS |
|---|---|---|---|
| 3000 | 0.231 | - | - |
| 1000 | 0.234 | 0.24 | 0.24 |
| 30000 | 0.209 | - | 0.238 |
Figures ?? give the DSP of the stream-wise velocity component for the three first rows and LES and EB-RSM when available at a point situated in the mid-plane at a normal distance from the pin surface equals to 0.03D. The experimental value is represented on the graphs for pin 1. For Pin 1, both LES computations at and exhibit more than one peak. Although a peak is observed around the frequencies mentioned by Ames et al. the most energetic one is above St=0.3. The DSP around Pin 2 shows frequencies similar to those observed around Pin 1 but with much higher r.m.s. values. Pin 3 has different behavior at the two Reynolds numbers. At , more energy is present at low frequencies but one still observes the peak arount St=0.35. At , the spectrum behavior looks like the one observed around the first two pins. The wall resolved Reynolds stress model shows similar results to LES for the first two pins at , exhibiting two peaks, the highest one being around St=0.3. Note that the resolved energy is naturally smaller than the one observed in LES and than the peak of tfirst frhe equency, closer to the one observed experimentally, is close to the second one in terms of amplitude. Around Pin 3 and at the freqencies move to lower values (as it was the case with LES at a lower Reynolds number). At , the EB-RSM shows one peak for the first pin close to the observed experimental value. The second pins exhibits a much higher frequency (the double of the previous one) with much more energy at low frequencies. Then, pin shows a change in the energetic content as the most energetic frequencies are at lower values (0.1 to 0.2).
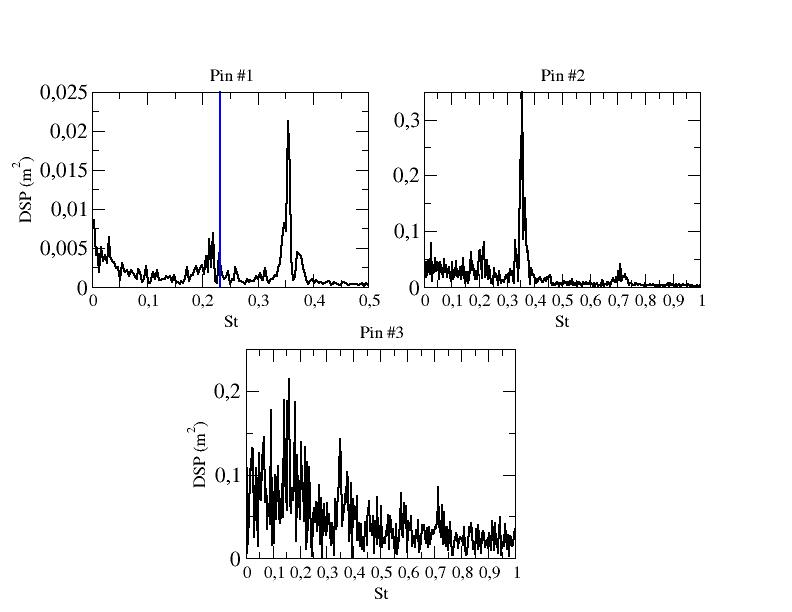
Figure ??: DSP of the stream-wise velocity component at a distance equal to 0.03D normal to the pins and in the mid-plane - Pins 1, 2 and 3 - - black: LES, blue: Ames et al. exp.

Figure ??: DSP of the stream-wise velocity component at a distance equal to 0.03D normal to the pins and in the mid-plane - Pins 1, 2 and 3 - - black: LES, red: EB-RSM, blue: Ames et al. exp.

Figure ??: DSP of the stream-wise velocity component at a distance equal to 0.03D normal to the pins and in the mid-plane - Pins 1, 2 and 3 - - red: EB-RSM, blue: Ames et al. exp.
Nusselt number on the bottom wall
Figures ?? show the Nusselt number normalized by its averaged value over the bottom wall for the 8 rows. LES comptations uexhibit an excellent behaviour compared to experimental values. The Nusselt number seems however overestimated at the horseshoe vortices locations and underestimated in the wake of the third row, in particular at the highest Reynolds number. One recalls here than the error made on the average of the normalized Nusselt number is equal to 3% and 1% for and , respectively.
The φ-model and the kω-SST are inapt in predicting the physics and thus local quantities such as the Nusselt number.
The EB-RSM exhibits a very satisfactory global behaviour,r in particular at the highest Reynolds numbe. The Nusselt number is however underestimated in the wake of the first cylinder as the unsteadiness is lower than LES one. The prediction of the next rows is satisfactory although an overestimation of heat transfer in the wake of the cylinders for the last 4 rows is observed.
Figures ?? show detailed profiles of the normalized Nusselt number along particular lines (see "Test Case Studies" section) for all the models. LES exhibits excellent results in particular after the second pin. The EB-RSM, shows some discrepencies for and very good results at in particular starting from row 5 (where the statistically periodic behavior is supposed to be reached).

Figure ??: Local Nusselt number on the bottom wall - LES computation at vs. experimental results from Ames et al.
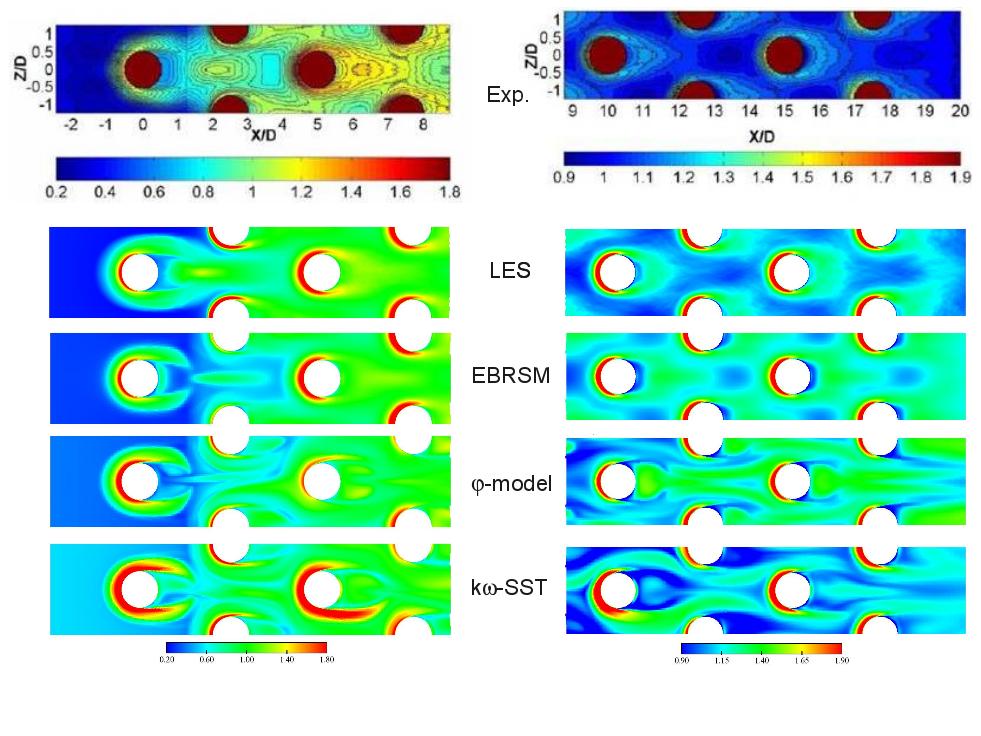
Figure ??: Local Nusselt number on the bottom wall - LES and URANS computations at vs. experimental results from Ames et al.
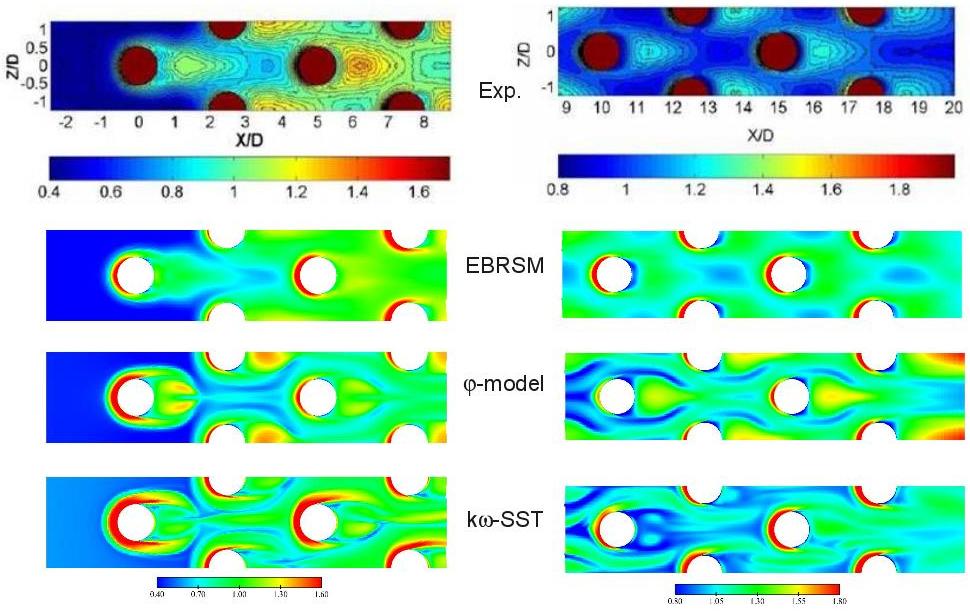
Figure ??: Local Nusselt number on the bottom wall - URANS computations at vs. experimental results from Ames et al.

Figure ??: Local Nusselt number on the bottom wall - - top: Y=0, bottom: Y=1.25 - symb.: Exp. - black: LES
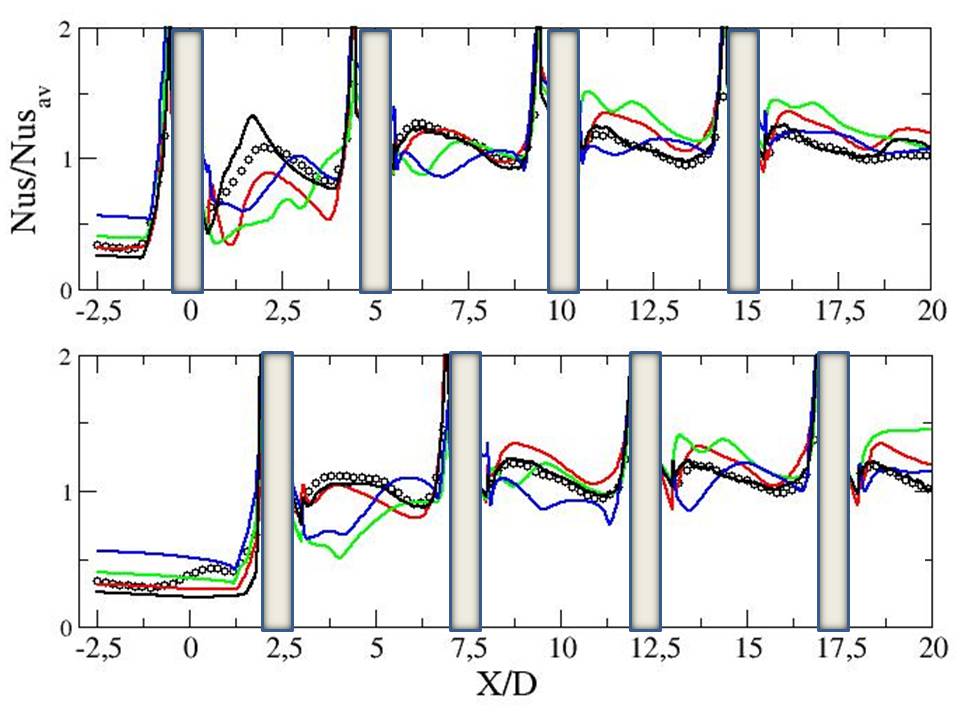
Figure ??: Local Nusselt number on the bottom wall - - top: Y=0, bottom: Y=1.25 - symb.: Exp. - black: LES - red: EBRSM - blue: Phi-model - green: kw-SST

Figure ??: Local Nusselt number on the bottom wall - - top: Y=0, bottom: Y=1.25 - symb.: Exp. - red: EBRSM - blue: Phi-model - green: kw-SST
Contributed by: Sofiane Benhamadouche — EDF
© copyright ERCOFTAC 2024

















