UFR 4-10 Test Case: Difference between revisions
| Line 74: | Line 74: | ||
'''''Treatment of Reynolds stresses''''' | '''''Treatment of Reynolds stresses''''' | ||
The approaches adopted in representing the turbulent stresses appearing in the momentum equations can largely be divided into three groups: ''linear eddy-viscosity models'' (EVM), ''algebraic-stress'' (ASM) or ''non-linear models'' and full ''Reynolds-stress transport models'' (RSTM). The vast majority of EVM publications in this context are based on variants of the ''k-''ε model, examples being Betts and | The approaches adopted in representing the turbulent stresses appearing in the momentum equations can largely be divided into three groups: ''linear eddy-viscosity models'' (EVM), ''algebraic-stress'' (ASM) or ''non-linear models'' and full ''Reynolds-stress transport models'' (RSTM). The vast majority of EVM publications in this context are based on variants of the ''k-''ε model, examples being Betts and Dafa’Alla [4], Davidson [14] and Ince and Launder [38], with LRN wall treatments, and Markatos and Pericleous [47] and Thompson ''et al''. [59] with wall functions. Examples of the ASM approach include Humphrey and To [37], Davidson [15], Shabbir and Taulbee [58], Muramatsu and Ninokata [49], Liu and Wen [45] and Wen ''et al.'' [65]. The application of full RSTMs in this context has been relatively rare however examples include: Dol ''et al''. [19], Chang and Bottoni [8] and Boudjemadi ''et al.'' [6]. | ||
'''''Treatment of turbulent heat fluxes''''' | '''''Treatment of turbulent heat fluxes''''' | ||
The simplest representation used for the turbulent heat fluxes is to assume a linear isotropic form, analogous to Fourier's law, with the eddy diffusivity calculated from the eddy viscosity using the assumption of a constant turbulent Prandtl number (''Pr<sub>t</sub>''). This appears in some earlier studies ''e.g''. Betts and Dafa’Alla [4], Davidson [14] and Markatos and Pericleous [47] however it has fallen out of favour due to the importance of counter-gradient diffusion effects in turbulent buoyant flows [42]. Another gradient-based approach commonly used is the generalised gradient-diffusion hypothesis (GGDH) of Daly and Harlow, see [41], which does not assume a constant ''Pr<sub>t</sub>'', one example being the study of Ince and Launder [38]. More sophisticated approaches use one- or two-equation models for the transport and production/destruction of the temperature variance, <math>\bar{\theta}^2</math> [[Image:U4-10d32_files_image032.gif]] (analogous to the turbulence kinetic energy) and its dissipation rate, ε. These can either be used to calculate a single isotropic eddy diffusivity, as in the model of Abe ''et al.'' [1], or combined with anisotropic algebraic expressions for the turbulent heat fluxes, as in the algebraic-flux models (AFM) of Hanjalić ''et al.'' [30-33]. | The simplest representation used for the turbulent heat fluxes is to assume a linear isotropic form, analogous to Fourier's law, with the eddy diffusivity calculated from the eddy viscosity using the assumption of a constant turbulent Prandtl number (''Pr<sub>t</sub>''). This appears in some earlier studies ''e.g''. Betts and Dafa’Alla [4], Davidson [14] and Markatos and Pericleous [47] however it has fallen out of favour due to the importance of counter-gradient diffusion effects in turbulent buoyant flows [42]. Another gradient-based approach commonly used is the generalised gradient-diffusion hypothesis (GGDH) of Daly and Harlow, see [41], which does not assume a constant ''Pr<sub>t</sub>'', one example being the study of Ince and Launder [38]. More sophisticated approaches use one- or two-equation models for the transport and production/destruction of the temperature variance, <math>\bar{\theta}^{\ 2}</math> [[Image:U4-10d32_files_image032.gif]] (analogous to the turbulence kinetic energy) and its dissipation rate, ε. These can either be used to calculate a single isotropic eddy diffusivity, as in the model of Abe ''et al.'' [1], or combined with anisotropic algebraic expressions for the turbulent heat fluxes, as in the algebraic-flux models (AFM) of Hanjalić ''et al.'' [30-33]. | ||
== Large-eddy simulations == | == Large-eddy simulations == | ||
Revision as of 08:07, 28 September 2011
Natural convection in simple closed cavity
Underlying Flow Regime 4-10 © copyright ERCOFTAC 2004
Test Case
Brief description of the study test case
The test case chosen consists of measurements of turbulent buoyancy-driven flow in a tall cavity carried out by Betts and Bokhari [3, 5] at UMIST. This case was one of those considered in the 5th ERCOFTAC/IAHR Workshop on Refined Flow Modelling in 1996 [24]. The measurement data are available in the ERCOFTAC database:Case 79 or directly from UMIST: http://cfd.me.umist.ac.uk/tmcfd/expdata/bettbok.html. Conditions at the mid-height of the cavity approximate to those in an infinitely tall cavity, allowing comparison at that location with the DNS data ofBoudjemadi et al. [6] and Versteegh and Nieuwstadt [63] (see http://tmdb.ws.tn.tudelft.nl/workshop5.html). It should be noted that the DNS data do not agree with each other in all respects and also do not agree fully with the experimental data for some quantities. Dol et al. [19] judged the data of [63] to be the more reliable of the two DNS data sets.
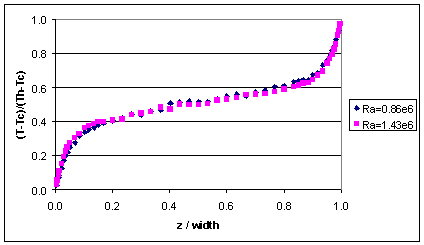
The experiments were undertaken to investigate the natural convection of air in a tall differentially-heated rectangular cavity (2.18m high by 0.076m wide by 0.52m in depth, aspect ratio 28.6:1) shown diagrammatically in Figure 5(a). They were performed with temperature differentials between the vertical plates of 19.6 and 39.9 °C, giving Rayleigh numbers based on the width of 0.86x106 and 1.43x106, respectively. The non-dimensional temperature differences, θ, are 0.033 and 0.064, respectively, placing the flow well within the Boussinesq regime. The resulting mean Nusselt numbers across the cavity are 5.85 for the lower Ra and 7.57 for the higher. Under these conditions the flow in the core of the cavity is fully turbulent and property variations with temperature are comparatively small. The temperature and flow fields were found to be closely two-dimensional, except close to the front and back walls, and anti-symmetric across the diagonal of the cavity (as should be the case given the low temperature differential). The differing thermal stratification across the top and bottom walls observed in many earlier experiments has been removed.
Some key features of the experimental set up are as follows:
- Active walls effectively isothermal;
- Internal surface temperatures of top and bottom walls vary smoothly;
- Low heat loss through front and back walls;
- Depth sufficient to produce well-defined two-dimensional flow on mid-plane.
Test Case Experiments
A previously used experimental rig (that of Betts and Dafa’Alla [4, 13]) was modified by fitting partially conducting top and bottom walls and outer guard channels, to provide boundary conditions which avoid the inadequately defined sharp changes in temperature gradient and other problems associated with insufficient insulation on nominally adiabatic walls. Mean and turbulent temperature and velocity variations within the cavity have been measured, together with heat fluxes and turbulent shear stresses. The partially conducting roof and floor provide locally unstable thermal stratification in the wall jet flows there, which enhances the turbulence as the flow moves towards the temperature controlled plates. The results provide a greatly improved benchmark for the testing of turbulence models in this low turbulence Reynolds number flow. Profiles of mean vertical velocity are given in Figure 5(b) for the Ra=0.86 x 106 case and of the mean temperature at mid-height for both Ra values in Figure 6.
Experimental rig
The experimental rig consists of two polished aluminium vertical walls backed by water jackets (water passing upwards on both sides) with independent temperature controls. The vertical walls are oversized relative to the internal cavity dimensions so as to ensure isothermal conditions over the full internal height. The water jacket on the hot wall is 10mm thick and backed by 1cm thick closed-cell thermo-flux insulating material bolted to a wooden frame. Both water jackets are backed by 5cm thicknesses of polystyrene. The passive front and back walls consist of 9.5mm acrylic sheets and are intended to be close to adiabatic. It was not possible to provide full internal guard cavities however each of the acrylic walls was clamped by two vertical stainless steel hollow channels (one hot and one cold). Water from the same tanks as used for the hot and cold walls is circulated through these channels and the whole assembly is backed by 5cm polystyrene slabs.
The top and bottom walls consist of 5cm natural hard rubber with a layer of 35 thermocouples imbedded at mid-thickness. They are wedged between the active walls with good thermal contact ensured by a layer of heat-conducting grease. The outer sides of the rubber walls are covered by 10cm of polystyrene and the inner sides by a thin sheet of adhesive aluminium foil to reduce radiation absorption. The thermal conductivity of the rubber (0.155 W/mK) is close to the effective mean conductivity across the cavity under turbulent conditions. As well as providing well-defined boundary conditions, the use of the rubber also provides unstable thermally-stratified layers adjacent to both the roof and the floor which act to oppose re-laminarisation.
Instrumentation
The temperature measurements were carried out using K-type thermocouples with response times of 0.065 or 0.07 seconds. These were located in the water jackets, guard channels, rubber roof and floor and outside the passive walls. The temperatures within the fluid were measured using a single traversed thermocouple with access via sealed slots in one of the acrylic walls. The velocity measurements were carried out using a single-component laser-doppler velocimetry (LDV) system. This used a 15mW He-Ne laser in forward-scatter mode with dual Bragg shift and a beam expander which produced a probe volume of diameter 0.37mm and length 4mm. Seeding was from a burning joss stick injected for 2-3 minutes and left to settle for an hour giving a particle size of order 1mm. Optical access is gained via the acrylic walls, locally removing a minimal amount of insulation. Spectral analyses of both the temperature and velocity records were carried out which indicated that the high frequency cut off and the signal-processing methods employed had a negligible effect on the recorded rms values.
 |
 |
|
Figure 5: (a) Schematic diagram of experimental arrangement. (b) Profiles of vertical velocity at different heights in the cavity for Ra=0.86 x 106 (symbols experiment). | |
CFD Methods
The major challenge in attempting to model transitional or fully-turbulent flows in simple cavities is the choice of an appropriate representation for the turbulence effects. The vast majority of publications considering such flows to date have employed a Reynolds-averaged (RANS) approach, requiring the use of some form of turbulence model for closure. For this reason this review will focus mainly on the various RANS approaches adopted, which are outlined in the section on Renolds-averaged approaches below. An increasing number of workers are now applying large-eddy simulation techniques to buoyant cavity flows and some examples of these are reviewed briefly in the section on Large-Eddy simulations below.
As the physics of turbulent buoyant flows, even for this simple test case, are highly complex it is difficult to draw absolute conclusions concerning best practice as often simple models can give reasonable solutions for the wrong reasons. Of particular importance are the counter-gradient diffusion effects typical of heat transfer buoyant flows which can lead to finite turbulent heat fluxes even in the absence of a mean temperature gradient.
Reynolds-averaged approaches
In the RANS approach to modelling turbulent buoyant flows, three particular issues must be dealt with, namely: the treatment of walls, the representation of the turbulent Reynolds stresses and the representation of the turbulent heat fluxes. These will now be considered one by one.
Wall treatment
Early attempts, e.g. [16, 47, 59], applied the standard high-Re k-ε model to turbulent cavity flows, using wall-function boundary conditions. This approach tends to overpredict the heat transfer rate and cannot predict laminarisation [34, 35]. While some specialised wall functions for buoyant flows have been developed [26] these have tended to be quite restrictive. The majority of models applied to the present case have integrated up to the wall using some form of low-Reynolds-number (LRN) treatment with damping functions. The advantage of this approach is that it can predict laminarisation and is potentially more general than the wall-function approach. Examples of its application are [4, 14, 34, 38], among many others.
Treatment of Reynolds stresses
The approaches adopted in representing the turbulent stresses appearing in the momentum equations can largely be divided into three groups: linear eddy-viscosity models (EVM), algebraic-stress (ASM) or non-linear models and full Reynolds-stress transport models (RSTM). The vast majority of EVM publications in this context are based on variants of the k-ε model, examples being Betts and Dafa’Alla [4], Davidson [14] and Ince and Launder [38], with LRN wall treatments, and Markatos and Pericleous [47] and Thompson et al. [59] with wall functions. Examples of the ASM approach include Humphrey and To [37], Davidson [15], Shabbir and Taulbee [58], Muramatsu and Ninokata [49], Liu and Wen [45] and Wen et al. [65]. The application of full RSTMs in this context has been relatively rare however examples include: Dol et al. [19], Chang and Bottoni [8] and Boudjemadi et al. [6].
Treatment of turbulent heat fluxes
The simplest representation used for the turbulent heat fluxes is to assume a linear isotropic form, analogous to Fourier's law, with the eddy diffusivity calculated from the eddy viscosity using the assumption of a constant turbulent Prandtl number (Prt). This appears in some earlier studies e.g. Betts and Dafa’Alla [4], Davidson [14] and Markatos and Pericleous [47] however it has fallen out of favour due to the importance of counter-gradient diffusion effects in turbulent buoyant flows [42]. Another gradient-based approach commonly used is the generalised gradient-diffusion hypothesis (GGDH) of Daly and Harlow, see [41], which does not assume a constant Prt, one example being the study of Ince and Launder [38]. More sophisticated approaches use one- or two-equation models for the transport and production/destruction of the temperature variance, ![]() (analogous to the turbulence kinetic energy) and its dissipation rate, ε. These can either be used to calculate a single isotropic eddy diffusivity, as in the model of Abe et al. [1], or combined with anisotropic algebraic expressions for the turbulent heat fluxes, as in the algebraic-flux models (AFM) of Hanjalić et al. [30-33].
(analogous to the turbulence kinetic energy) and its dissipation rate, ε. These can either be used to calculate a single isotropic eddy diffusivity, as in the model of Abe et al. [1], or combined with anisotropic algebraic expressions for the turbulent heat fluxes, as in the algebraic-flux models (AFM) of Hanjalić et al. [30-33].
Large-eddy simulations
An increasing number of large-eddy simulations of turbulent buoyant flows are being published, though a number of issues remain to be fully resolved, for example the treatment of energy backscatter. One early study is that of Eidson regarding Rayleigh-Benard convection [22], more recent examples are the work of Schumann [57], Canuto et al. [7] and Peng and Davidson [55, 56]. A variety of sub-grid scale models have been applied including the Smagorinsky and dynamic models and some specific buoyancy modifications have been proposed.
© copyright ERCOFTAC 2004
Contributors: Nicholas Waterson - Mott MacDonald Ltd
