UFR 3-35 Evaluation: Difference between revisions
| Line 108: | Line 108: | ||
== Distribution of turbulent kinetic energy and its budgets terms: Production, Transport and Dissipation == | == Distribution of turbulent kinetic energy and its budgets terms: Production, Transport and Dissipation == | ||
=== Turbulent kinetic energy === | === Turbulent kinetic energy === | ||
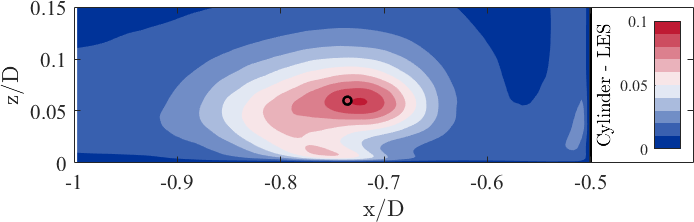
[[File:UFR3-35_PIV_TKE.png|centre|frame|Turbulent kinetic energy <math> \langle k_{\mathrm{PIV}}\rangle = 0.5 | [[File:UFR3-35_PIV_TKE.png|centre|frame|Turbulent kinetic energy <math> \langle k_{\mathrm{PIV}}\rangle = 0.5(\langle u'^2\rangle+\langle w'^2\rangle)/u_{\mathrm{b}^2}</math>]] | ||
[[File:UFR3-35_LES_TKE.png|centre|frame|Turbulent kinetic energy <math> \langle k_{\mathrm{LES}}\rangle = 0.5 | [[File:UFR3-35_LES_TKE.png|centre|frame|Turbulent kinetic energy <math> \langle k_{\mathrm{LES}}\rangle = 0.5(\langle u'^2\rangle+\langle w'^2\rangle)/u_{\mathrm{b}^2}</math>]] | ||
== Horizontal profiles of the pressure coefficient <math> c_{\mathrm{p}}(x) </math>, and of the friction coefficient <math> c_{\mathrm{f}}(x) </math> == | == Horizontal profiles of the pressure coefficient <math> c_{\mathrm{p}}(x) </math>, and of the friction coefficient <math> c_{\mathrm{f}}(x) </math> == | ||
Revision as of 16:58, 26 August 2019
Cylinder-wall junction flow
Evaluation
The evaluation of the numerical and experimental data sets in the symmetry plane upstream a wall-mounted cylinder refers to the time-averaged flow fields indicated by:
- the streamlines
- the location of the characteristic flow structures
- selected vertical and horizontal profiles of the velocity components and as well as the Reynolds sresses and the trubulent kinetic energy
- the distribution of the turbulent kinetic energy and its buget terms such as production, transport, and dissipation
- horizontal profiles of the pressure coefficient , and the friction coefficient
,
Streamlines
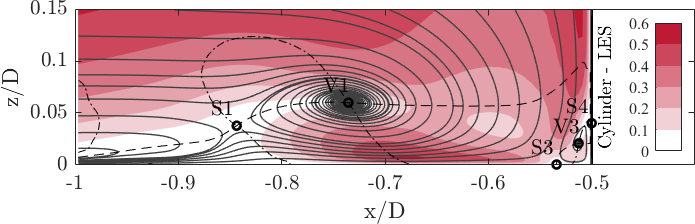
The streamlines of the PIV and the LES data show high similarity and agree well with each other. The plots are flooded with the normalized magnitude of the velocity field in the symmetry plane, thus . The approaching turbulent boundary layer is redirected downwards at the flow facing edge of the cylinder caused by a vertical pressure gradient. This downflow reaches the bottom plate of the flume at the stagnation point S3. Here, it becomes redirected (i) in the out-of-plane direction bending around the cylinder; (ii) towards the cylinder rolling up and forming the corner vortex V3; and (iii) in the upstream direction accelerating and fomring a wall-parallel jet. Due to the strong acceleration of the jet, a high vertical velocity gradient is exerted onto the bottom plate, which induces high wall shear stress. Parts of the approaching boundary layer is dragged downwards forming the horseshoe vortex V1. Upstream of thsi vortex system, the approaching flow is blocked and recirculates, and as a consequence a saddle point S1 with zero velocity magnitude appears.
Location of the characteristic flow structures
The position of the characteristic flow structures highlited in the streamline plots is listed in the following table
| PIV | LES | |||
|---|---|---|---|---|
| S1 | ||||
| S2 | ||||
| S3 | ||||
| S4 | ||||
| V1 | ||||
| V3 |
Horizontal and vertical profiles of the velocity components and Reynolds stresses
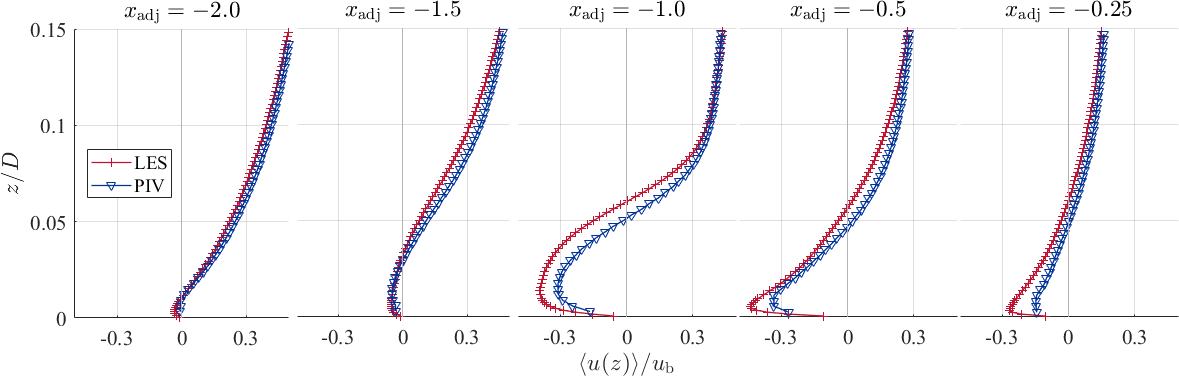
The vertical profiles are extracted at the following positions with respect to the time-averaged position of the horseshoe vortex, and can be found in the following plot.
Since the flow structure of the LES and the PIV is slightly different, we use an adjusted coordinate, in order to compare the data at the same position in the flow. The coordinate is defined as follows:
,
with , such that represents the time-averaged location of the horseshoe vortex centre .
The vertical velcoity profiles are presented at the seleted locations. When the downflow is deflected at the bottom plate at , the wall-parallel jet starts to develop, and consequently, the flow accelerates. At , a near-wall velocity peak appears, which becomes more pronounced in the upstream direction (see ). In this region, the wall shear stress reaches on one hand its maximum value and on the other hand reveals a plateau-like shape. This means that the largest values of the gradient appear. Underneath the horseshoe vortex, the flow decelerates and the wall-peak of the velocity lifts from the bottom plate and becomes less distinct. Further upstream, the near-wall peak of the streamwise velocity disappears and therefore, the wall-parallel jet fades out. Due to the evaluation of the PIV images by an interrogation window based cross correlation, the strong gradient at the wall cannot be fully resolved, and therefore, the near-wall peak of the streamwise velocity is damped in the experimental data.
The vertical profiles of the Reynolds stresses and the resulting turbulent kinetic eneryg is presented only at , , and . The accelerating jet is again indicated by a near wall peak of the stress, while the horseshoe vortex leaves its footprint in the stresses and as (local) peak at . The shear stress distribution inside the wall-paralle jet is negative (in average) according to the flow direction (in average). The experimental and numerical data agree with each other both in amplitude as well as in shape. Again, the quality of the PIV data near the wall is underminded by the strong gradients being evaluated using interrogation windows.
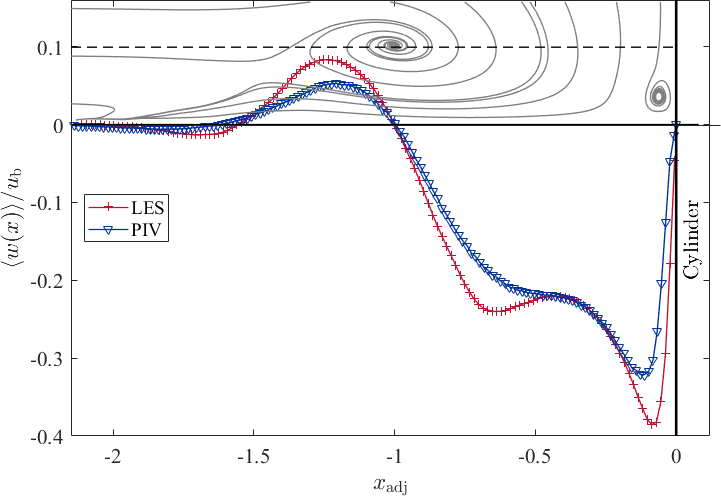
Analysing the profile of the vertical velocity component along the axis at the height of the horseshoe vortex, reveals on the one hand the clockwise rotation of the vortex, and on the other hand two minima between the horseshoe vortex and the cylinder. At , the peak in the downwards directed flow stems from the downflow, while the second local minimum at approximately represents the downwards rotation of the horseshoe vortex. Both data agree well in shape. However, the LES data indicate higher amplitudes in general.
The Reynolds stresses and the turbulent kinetic energy at the height of the horseshoe vortex show similar distributions. At the centre of the vortex, the normal stresses, and consequently the turbulent kinetic energy as well, reveal a peak, which wears off in the up- and downstream direction. In addition, the downflow close to the cylinder surface generates stresses as well. The shear sresses play a minor role in the region between the cylinder and the horseshoe vortex, while they become negative upstream of the horseshoe vortex indicating the interference of the approaching flow wiht the horseshoe vortex.
Distribution of turbulent kinetic energy and its budgets terms: Production, Transport and Dissipation
Turbulent kinetic energy
Horizontal profiles of the pressure coefficient , and of the friction coefficient
The pressure coefficient is computed as:
,
while the friction coefficient is determined as:
.
The following plots were taken from the LES data only since the pressure is not contained in the PIV data and the spatial resolution appeared to be too corase to calculate the wall shear stress, thus the friction coefficient, correctly. The first data point in the experimental data could be obtained at . In the LES, the first grid point was at , which is about a factor of 7 finer than the experimental results. Additionally, a thinned streamline plot is given for the sake of better orientation in a qualitative sense showing the positions in the direction in which the profiles were extracted. The red symbols refer to the profiles near the wall indicated by the red solid line, whereas the blue symbols and the blue solid line refer to the profile at the height of the horseshoe vortex.
At the stagnation point S3, the pressure coefficient reaches a maximum value of about due to the downflow impinging at the bottom of the flume. The downflow is deflected in all directions forming an accelerating wall-parallel jet in particular in the uptream direction. The acceleration is indicated by the decrease of the pressure coefficient. At , underneath the horseshoe vortex, the pressure coefficient shows a kink and the rate of decreases is less significant than before.
The accelerating wall-parallel jet is also recognisable in the distribution of the friction ceofficient . From the stagnation point S3 on, with zero wall shear stress, the friction coefficient reveals a sharp peak underneath the foot vortex V3. In the upstream direcion, the wall shear stress increases due to the accelerating jet until a plateau is reached. Here, the friction coefficient is almoust constant at , which represents the maximum absolute value. It should be noted that the maximum is not located underneahth the horseshoe vortex. The distribution of is dominated by the wall-parallel jet rather than by the horseshoe vortex. Further upstream, the value of is small but negative, indicating the fading near-wall jet pointing still in the upstream direction. Unlike Apsilidis et al. (2015), we could not observe a second vortex here.
Following the downflow towards the bottom plate of the flume, the pressure increases with decreasing distance to the bottom. The pressure coefficient increases likewise. Therefore, near the cylinder surface, the pressure coefficient shows a high amplitude at the height of the horseshoe vortex. Along a horizontal axis at , decreases reaching its minimum value of about coinciding with the centre of the horseshoe vortex. Upstream of the horseshoe vortex, the horizontal profiles of the pressure coefficient coincide with each other irrespectively of the wall distance.
Contributed by: Ulrich Jenssen, Wolfgang Schanderl, Michael Manhart — Technical University Munich
© copyright ERCOFTAC 2019