Evaluation AC3-08: Difference between revisions
No edit summary |
David.Fowler (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
{{AC|front=AC 3-08|description=Description_AC3-08|testdata=Test Case_AC3-08|cfdsimulations=CFD Simulations_AC3-08|evaluation=Evaluation_AC3-08|qualityreview=Quality Review_AC3-08|bestpractice=Best Practice Advice_AC3-08|relatedUFRs=Related UFRs_AC3-08}} | |||
='''Spray evaporation in turbulent flow'''= | ='''Spray evaporation in turbulent flow'''= | ||
| Line 97: | Line 99: | ||
Site Design and Implementation: [[Atkins]] and [[UniS]] | Site Design and Implementation: [[Atkins]] and [[UniS]] | ||
{{AC|front=AC 3-08|description=Description_AC3-08|testdata=Test Case_AC3-08|cfdsimulations=CFD Simulations_AC3-08|evaluation=Evaluation_AC3-08|qualityreview=Quality Review_AC3-08|bestpractice=Best Practice Advice_AC3-08|relatedUFRs=Related UFRs_AC3-08}} | |||
Revision as of 10:12, 19 March 2009
Spray evaporation in turbulent flow
Application Challenge 3-08 © copyright ERCOFTAC 2004
Comparison of Test data and CFD
Several results of the numerical calculations were presented by Kohnen (1997), Kohnen and Sommerfeld (1998) and Sommerfeld (1998). The profiles of the droplet velocity and the droplet mass flux could be predicted reasonably well. The calculated droplet number mean diameter showed some larger differences compared to the measurements, especially at the edge of the spray.
For a comparison of the calculations with the measurements the properties of the droplet phase for case 2 are considered. The profiles of the axial and radial mean velocities shown in Fig. 5 are obtained by averaging over the entire droplet size spectrum at each location. The agreement between measurement and computation is reasonably good for both velocity components. However, the radial spread of the spray is slightly under-predicted which is obvious from the droplets` radial mean velocity profiles (Fig. 5 b). Moreover, the recirculation region developing downstream of the nozzle holder is not properly resolved by the calculations as seen from the velocity profiles at z = 25 mm.
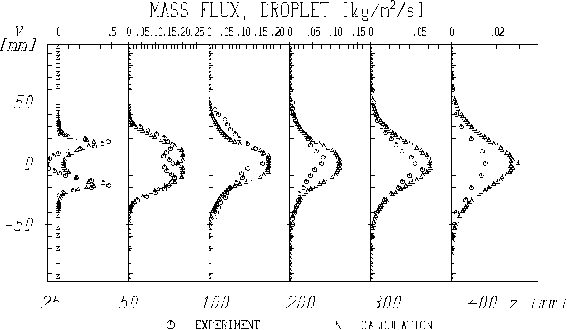
These observations have also consequences for the prediction of the droplet mass flux in the z-direction shown in Fig. 6. For most of the profiles the droplet mass flux in the core of the spray is over-predicted. This also may be an indication for an under-prediction of the evaporation rate. By integrating the profiles of the droplet mass flux and assuming an axial-symmetric flow, one may obtain the droplet mass flow rate along the test section (for case 2 shown in Fig. 8 b). Comparing measurement and prediction for the normalised droplet mass flow rate reveals, that the decrease of this property due to evaporation is more or less properly captured by the calculations. Between z = 200 and 400 mm the liquid mass flow rate is slightly over-predicted as may be expected from the mass flux profiles (Fig. 6). The differences between measurement and calculation may be associated with slight asymmetries of the spray in the experiment and probably the effects of temperature and vapour concentration fluctuations on droplet evaporation which were not accounted for in the present calculations.
Fig. 5 Comparison of measurement and calculation for an evaporating spray, a) axial droplet mean velocity profiles, b) radial droplet mean velocity profiles (case 2, Table 1)
Fig. 6 Profiles of droplet mass flux, comparison of measurement and calculation (case 2, Table 1)
Fig. 7 Profiles of droplet number mean diameter, comparison of measurement and calculation (case 2, Table 1)
The profiles of the droplet number mean diameter (Fig. 7) reveal some feature which was also found previously for the other test cases, namely the over-prediction of the droplet mean size at the edge of the spray. This might have different sources related to the measurements and the modelling. Measurement errors by phase-Doppler anemometry may result from non-spherical droplets which are likely to be present close to the nozzle exit where in the present study the inlet conditions were measured. Moreover, fluctuations in gas temperature and vapour concentration may be responsible for this discrepancy. In addition, droplet oscillations can enhance droplet evaporation. This effect was analysed by Daidzic et al. (1995) and found to be quite important at the edge of the spray were the droplet diameters are larger. Depending on the mode of oscillation considered, the agreement of the calculations with the measurements could be considerably improved. Further studies of these effects described above are however required.
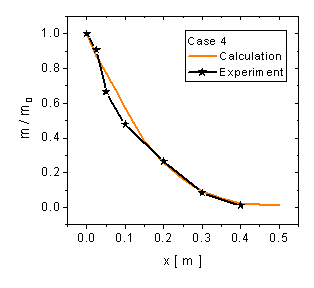
A further comparison of the numerical predictions with the measurements is based on the normalised liquid mass flow rate along the test section for all four test cases (Fig. 8). It is obvious, that the best agreement is achieved for case 1 and 4. In case 2 some fluctuations of the measured mass flow rate are visible which is most likely due to asymmetries of the spray. For case 2 the measured evaporation rate is higher than the predicted values.
With the applied modelling approach on the basis of the Euler/Lagrange method reasonable agreement between computations and measurements could be achieved for the gas and droplet phase. Further improvements might be possible with use of a full Reynolds stress turbulence model together with a more advanced droplet dispersion model (e.g. Langevin model). Additionally, a more advanced droplet evaporation model might be used by accounting for the temperature distribution inside the droplet.
Fig. 8 Normalised droplet mass flow down the test section obtained by integrating the profiles of the droplet mass flux, comparison of calculation and measurement for: a) case 1, b)case 2, c) case 3, d) case 4
References
Abramzon, B. and Sirignano, W. A. Droplet vaporization model for spray combustion calculations. Int. J. Heat Mass Transfer, 32, 1605-1618, 1989
Daidzic, N., Kohnen, G. and Sommerfeld, M. A new droplet evaporation model based on interfacial phenomena. Proceedings of the Second International Conference on Multiphase Flows, Kyoto, Japan, April 1995, Vol. 1, SP-23-SP-30 (1995)
Kohnen, G. Über den Einfluß der Phasenwechselwirkungen bei turbulenten Zweiphasenströmungen und deren numerische Erfassung in der Euler-Lagrange Betrachtungsweise. Dissertation, Martin-Luther-Universität Halle-Wittenberg, 1997
Kohnen, G. und Sommerfeld, M. Numerische Berechnung verdampfender Sprühnebel. Chemische Technik, Jahrg. 50, 225-234 (1998)
Launder B.E. and Spalding D.B. The numerical computation of turbulent flows. Comp. Meth. Appl. Mech. and Eng. Vol. 3, 269-289 (1974)
Perry: Chemical Engineers Handbook, 6th Edition (1984)
Sommerfeld, M. (Ed.) Proceedings 6th Workshop on Two-Phase Flow Predictions, Erlangen 1992, Bilateral Seminars of the International Bureau Forschungszentrum Jülich, (1993)
Sommerfeld, M., Kohnen, G. and Rüger, M. Some open questions and inconsistencies of Lagrangian Particle dispersion models. Ninth Symposium on Turbulent Shear Flows, Kyoto, Aug. 1993, Paper 15.1.
Sommerfeld, M. and Qiu, H.-H. Particle concentration measurements by phase-Doppler anemometry in complex dispersed two-phase flows. Experiments in Fluids, Vol. 18, 187-198 (1995)
Sommerfeld, M. and Qiu, H.-H. Experimental studies of spray evaporation in turbulent flows. International Journal of Heat and Fluid Flow, Vol. 19, 10-22 (1998)
Sommerfeld, M. Analysis of isothermal and evaporating sprays using phase-Doppler anemometry and numerical calculations. International Journal of Heat and Fluid Flow, Vol. 19, 173-186 (1998)
Vargaftik: Handbook of Physical Properties of Liquids and Gases, 2 nd Edition (1983)
VDI-Wärmeatlas, VDI-Verlag, 5th Edition (1988)
© copyright ERCOFTAC 2004
Contributors: Martin Sommerfeld - Martin-Luther-Universitat Halle-Wittenberg
Site Design and Implementation: Atkins and UniS