CFD Simulations AC7-02
Airflow in the human upper airways
Application Challenge AC7-02 © copyright ERCOFTAC 2020
CFD Simulations
Overview of CFD Simulations
Three LES (LES1-3) and one RANS simulation were carried out in the benchmark geometry at an air flowrate of 60 L/min.
This flowrate results in a Reynolds number of 4921 in the model’s trachea.
This is slightly higher than the Reynolds number in the experiments, due to the reasons discussed in section Measurement errors.
The details of the numerical tests are given in the following paragraphs.
In summary, the main differences between the simulations are:
1. Computational meshes: LES1&2 employ the same comp. meshes, whereas LES3 and RANS use different meshes.
2. Turbulence modeling: LES1 uses the dynamic version of the Smagorinsky-Lilly subgrid scale model, whereas LES2&3 employ the Wall-adapting eddy viscosity (WALE) SGS model.
In RANS simulations, the k-ω SST, standard k-ε and RNG k-ε turbulence model have been tested.
3. Discretisation method: LES1&2 and RANS use the Finite Volume approach whereas LES3 employs the Finite Element Method.
Large Eddy Simulations — Case LES1
Computational domain and meshes
The geometry used in the calculations is the same as the one used in the experiments developed by the group at Brno University of Technology (BUT). The computational domain, shown in figure 8, has one inlet and ten different outlets, for which appropriate boundary conditions must be specified in the simulations.
The digital model of the physical geometry was used to generate a proper computational mesh in order to perform the simulations.
For LES1, two meshes were generated to allow us to examine the sensitivity of the results to the mesh resolution.
The coarser mesh includes 10 million computational cells and the finer approximately 50 million cells.
In these meshes, the near-wall region was resolved with prismatic elements, while the core of the domain was meshed with tetrahedral elements.
Cross-sectional views of these meshes at seven stations are shown in figure 9.
A grid convergence analysis was carried out in order to determine the appropriate resolution for the simulations.
This analysis is presented in section Numerical accuracy.
Table 3 reports grid characteristics, such as the height of the wall-adjacent cells (), the number of prism layers near the walls, the average expansion ratio of the prism layers (), the total number of computational cells, the average cell volume (V) and the average and maximum y+ values.
The higher y+ values (above 1) are found near the glottis constriction and the bifurcation carinas, which are characterised by high wall shear stresses.
Solution strategy and boundary conditions — Airflow
LES were performed using the dynamic version of the Smagorinsky-Lilly subgrid scale model with localized filtering (Lilly, 1992; Zang et al., 1993) in order to examine the unsteady flow in the realistic airway geometries. Previous studies have shown that this model performs well in transitional flows in the human airways (Radhakrishnan & Kassinos, 2009; Koullapis et al., 2016). The airflow is described by the filtered set of incompressible Navier-Stokes equations,
where , p, , and are the filtered velocity component in the i-direction, the filtered pressure, the density and kinematic viscosity of air, and the subgrid-scale (SGS) turbulent eddy viscosity, respectively. The overbar denotes resolved quantities.
The governing equations are discretized using a finite volume method and solved using OpenFOAM, an open-source CFD code (OpenFOAM Foundation, 2013a,b). In this framework, unstructured boundary fitted meshes are used with a collocated cell-centred variable arrangement. The finite volume method in OpenFOAM is in general 2nd-order accurate in space, depending on the convection differencing scheme (CDS) used. Whenever possible (usually in the cases with lower Reynolds numbers), the 2nd-order linear CDS is used. The order of accuracy had to be decreased in some cases in order to stabilize the simulation. In these cases, the clippedLinear scheme was used, which provides a good compromise between the accuracy of the (2nd order) linear scheme and the stability of the (1st order) mid-point scheme (OpenFOAM Foundation, 2013b). The temporal derivative is discretized using backward differencing, which is is also second order accurate in time and implicit. To ensure numerical stability the time step used is at inhalation flowrate of 60 L/min. The non-linearity in the momentum equation is lagged in OpenFOAM (linearization of equation before discretisation). The system of partial differential equations is treated in a segregated way, with each equation being solved separately with explicit coupling between the results. In turbulent flow applications, where the time step is kept small enough to capture the smaller turbulent time scales, the pressure-implicit split-operator algorithm, or PISO-algorithm, is used.
At the inhalation flowrate of 60 L/min, the Reynolds number at the inlet, based on the inflow bulk velocity and inlet tube diameter, is , which lies in the turbulent regime. In order to generate turbulent inflow conditions, a mapped inlet, or recycling, boundary condition was used (Tabor et al., 2004). To apply this boundary condition, the pipe at the inlet was extended by a length equal to ten times its diameter, as shown in figure 10. The pipe section was initially fed with an instantaneous turbulent velocity field generated in a precursor pipe flow LES. During the simulation of the airway geometry, the velocity field from the mid-plane of the pipe domain was mapped to the extended pipe’s inlet boundary (figure 10 ). Scaling of the velocities was applied to enforce the specified bulk flow rate. In this manner, turbulent flow is sustained in the extended pipe section, and a turbulent velocity profile enters the mouth inlet. To match the experimental conditions, uniform pressure is prescribed in the simulations at the 10 terminal outlets. A no-slip velocity condition is imposed on the airway walls.
Numerical accuracy
The sensitivity of the calculations to the mesh resolution was tested and the results are presented in this section.
Figure 11 displays contours and profiles of the mean velocity magnitude at cross sections in the mouth-throat/trachea, the main bifurcation and the left/right bronchi for the two different meshes examined.
Good agreement is observed for the mean velocities between the coarse and fine meshes.
Slight deviations are found at station D1-D2, located just downstream of the glottis.
Airflow recirculation is evident at this station that is not well captured on the coarse mesh.
Figure 12 displays contours and profiles of the turbulent kinetic energy (TKE) at cross sections in the mouth-throat/trachea, the main bifurcation and the left/right bronchi for the two different meshes examined. TKE is calculated as:
Higher levels of TKE are recorded on the finer mesh. These are mainly generated in the shear layers. As observed from the 2D profiles, TKE peaks are underpredicted on the coarse mesh.
In conclusion, although the coarse mesh yields results that are in reasonable agreement with the finer mesh predictions, in the following comparisons between CFD and PIV measurements, the finer LES predictions are considered.
Large Eddy Simulations — Case LES2
Computational domain and meshes
The computational domain and the meshes employed in these simulations are the ones described in Section Computational domain and meshes.
Solution strategy and boundary conditions — Airflow
In LES2, an eddy-viscosity-type model following the Boussinesq hypothesis (Sagaut, 2006) is used to close the system of filtered Navier-Stokes equations, (2&3). The Wall-adapting eddy viscosity model (WALE) SGS model (Nicoud & Ducros, 1999) has been employed. This model is based on the square of the velocity gradient tensor. The SGS viscosity obtained with this model takes into account the strain and the rotation rate of the smallest resolved turbulent fluctuations. Some features of this model are its capability of switching off in two-dimensional flows and in laminar flows. It also has a cubic behaviour near walls with respect to the normal direction of the wall.
The CFD simulations presented in this section have been carried out using the in-house CFD software TermoFluids (Lehmkuhl et al., 2007), based on the finite volume method (FVM). This CFD code is parallel, highly scalable and designed to work in both structured and unstructured meshes. The convective term in the momentum equation (3) is discretized using a second order Symmetry-Preserving (SP) scheme (Verstappen & Veldman, 2003). This discretization scheme constructs an anti-symmetric discrete convective operator. This operator does not introduce artificial dissipation in the momentum equation, and therefore the kinetic-energy is preserved. The diffusive operator is discretized by means of a second-order Central Differencing Scheme (CDS). Both convective and diffusive operators are integrated explicitly by means of a one-leg second-order time-integration scheme (Trias & Lehmkuhl, 2011). This scheme includes a free-parameter allowing to adapt its stability region. The free-parameter is dynamically selected maximizing the stability region in function of the eigenvalues of the discrete operators. Moreover, this time-integration strategy also selects the optimal time-step at each iteration. The pressure-velocity coupling is solved by means of the Fractional Step projection method (Kim & Moin, 1985). The idea behind this technique is to split the momentum within two steps: a first explicit step where an intermediate velocity is obtained, followed by a second step where the pressure is solved implicitly and the intermediate velocity is corrected obtaining the physical divergence-free velocity field. The Poisson equation is solved by means of the iterative Conjugate-Gradient (CG) method with Jacobi diagonal scaling.
The presented case has an inlet flowrate Q=60 L/min, which falls within the turbulent regime. Therefore, in order to generate the turbulent velocity profile for the inlet section, an auxiliary simulation of a pipe with the same diameter as the inlet and periodic boundary condition in the streamwise direction have been employed. The velocity field generated at the mid-plane of the pipe is saved and later imposed at the inlet section of the simulation during running time. At the respiratory airways walls, the boundary condition is defined as no-slip. Regarding the outlets, two different conditions were employed. For the cases presented in section Mesh convergence analysis, a constant flowrate was fixed en each one of the outlets. On the other hand, for the cases solved in section Comparison of different LES subgrid-scale models and in Section Evaluation, the pressure is fixed at the ten outlets with a value equal to atmospheric pressure.
Numerical accuracy
Two of the main numerical aspects that will determine the accuracy of a CFD simulation employing a LES approach are the mesh and the turbulence model employed for the subgrid scales. Therefore, in the present section these two parameters have been analyzed in detail.
Mesh convergence analysis
The effects of the mesh on the simulation results are studied comparing the same experiment and geometry using two different meshes: a fine one with 50 million control volumes (CVs) and a coarse one with 10 million CVs (see section Computational domain and meshes). The results for both mean velocities and TKE () obtained with the two meshes are depicted in figure 13 and 14, respectively.
As can be seen in figure 13, the agreement for the mean velocities is very good between both meshes and the results are practically identical. On the other hand, some differences can be appreciated for TKE between the two studied meshes. As observed in the 2D profiles (figure 14), the fine mesh yields higher levels of TKE than the coarse one. However, both meshes are able to capture the same trend, obtaining the highest levels of TKE in the same positions, which belongs to the shear layer regions. Hence, it is clear that, although first order quantities are well captured by both meshes, special care must be taken if second order quantities must be reproduced accurately, since the latter are very sensitive to mesh resolution. In conclusion, sufficiently fine meshes must be employed in order to correctly capture second order quantities, although first order ones can be obtained accurately with coarser meshes. Obviously, the recommended grid-spacing in this kind of simulations will be the result of a compromise between accuracy and computational cost.
Comparison of different LES subgrid-scale models
In order to assess the influence of the subgrid-scale turbulence model in LES of airflow in the human upper airways, four different turbulence models were compared.
Besides the WALE model (Nicoud & Ducros, 1999) previously introduced, three additional turbulence models have been studied.
The first one is the model proposed by Smagorinsky (1963), based on the Prandtl mixing length applied to subgrid-scale modelling.
In this model the turbulent viscosity is proportional to the strain.
The second model is the variational multiscale (VMS) approach applied in WALE.
This method was originally formulated for the Smagorinsky model by Hughes et al. (2000).
Using this framework the modelling is confined to the effect of a small-scale Reynolds stress, in contrast to classical LES in which the entire SGS stress is modelled.
The latter is the model proposed by Verstappen known as the QR eddy-viscosity model (Verstappen et al., 2010; Verstappen et al., 2011).
This model is based on two invariants of the rate-of-strain tensor.
The method is computationally very efficient, switches off in the case of back-scattering, laminar and two-dimensional flows, and the subgrid turbulent viscosity is proportional to the cube with respect to the normal direction of the wall.
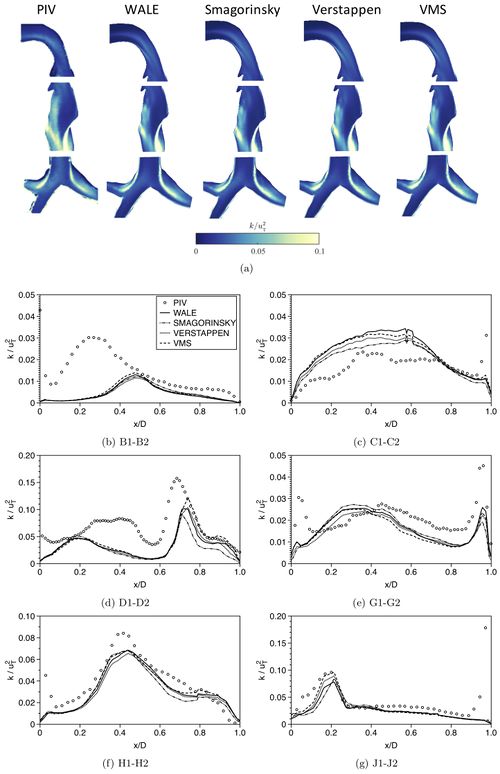
The results for the in-plane mean velocities and TKE (see section Evaluation and equations 8-11) are depicted in figure 15 and 16, respectively. As can be seen, the four models predict very similar results, except in shear layer regions for TKE levels (just downstream glottis constriction - station D), where some differences can be seen between the different models. However, these deviations are very small and not relevant. Therefore, it can be stated that all LES subgrid-scale models are able to provide results that are in reasonable agreement with the measurements.
Nonetheless, in previous works where different turbulence models in confined flows were compared, it was found that some turbulence models were not able to correctly predict the flow pattern. In the work of Muela et al. (2019), the Smagorinsky model was not able to correctly model the subgrid dissipation in the simulated confined flow, being too dissipative. The main difference to the cases examined in these works is the Reynolds number. In the present study, the Reynolds number in the trachea at 60 L/min is around Re = 4921, while the one of the case presented in Muela et al. (2019) is two orders of magnitude higher ().
In simulations of the airflow in the human upper airways, the Reynolds number is in most cases below Re < 10000 and therefore the flow is either laminar or with low turbulence. Due to that, the influence of the subgrid scales in this kind of flows is small, and the turbulence model is not as relevant as in more turbulent cases. Therefore, the turbulence model in simulations of the airflow in the human upper airways using LES modeling does not play a key role.
Large Eddy Simulations — Case LES3
Computational domain and meshes
Although the geometry used in the LES3 calculations is the same as the one used in the LES1&2 (shown in figure 8), the mesh employed in the LES3 simulations is different. It consists of 7 million linear finite elements (1.7 million degrees of freedom) including 3 layers of prismatic elements near the airway geometry walls. The adequacy of the employed mesh resolution is discussed in section Numerical Accuracy.
Solution strategy and boundary conditions — Airflow
Alya (Vazquez et al., 2016), which is a parallel multi-physics/multi-scale simulation code developed at the Barcelona Supercomputing Centre to run efficiently on high-performance computing environments is used in LES3. The convective term is discretized using a Galerkin finite element (FEM) scheme recently proposed (Charnyi et al., 2017), which conserves linear and angular momentum, and kinetic energy at the discrete level. Both second- and third-order spatial discretizations are used. Neither upwinding nor any equivalent momentum stabilization is employed. In order to use equal-order elements, numerical dissipation is introduced only for the pressure stabilization via a fractional step scheme (Codina, 2001), which is similar to approaches for pressure-velocity coupling in unstructured, collocated finite-volume codes (Jofre et al., 2014). The set of equations is integrated in time using a third-order Runge-Kutta explicit method combined with an eigenvalue-based time-step estimator (Trias & Lehmkuhl, 2011). This approach has been shown to be significantly less dissipative than the traditional stabilized FEM approach (Lehmkuhl et al., 2019). WALE SGS closure is used as LES model.
Atmospheric pressure and a laminar uniform velocity profile (zero turbulence) are applied at the mouth inlet of the model. At the 10 outlets of the model, zero-gradient pressure condition is imposed whereas the velocities are extrapolated from the boundary-adjacent cells using specified flow rates at each of the outlet. Although the outlet boundary condition in LES3 is different compared to the PIV setup, since the comparisons concern the proximal region of the model (mouth, trachea and main bifurcation) this mismatch is not expected to affect our findings. This is confirmed by the comparisons shown in section Evaluation.
Numerical accuracy
In order to assess the independence of LES3 results from grid resolution, a mesh convergence analysis was carried out. In the results presented in the following of this section, the computational domain was truncated at the end of the trachea and simulations were performed in the mouth-trachea region. Four computational meshes were generated, as shown in figure 17. Details of these meshes are reported in Table 4. Three meshes have identical resolution in the bulk region and different degrees of refinement of the near-wall prismatic elements (M1a-c). Mesh M2 has the finest resolution in both the bulk and near-wall regions. For the purpose of the mesh convergence analysis, the inlet conditions were different to the ones used in the simulation of the entire geometry for the LES3 case (i.e uniform velocity). Specifically, in order to generate a turbulent velocity profile for the inlet section, an auxiliary simulation of a pipe with the same diameter as the inlet and periodic boundary condition in the stream-wise direction have been employed. The velocity field generated at the mid-plane of the pipe is saved and later imposed at the inlet section of the simulation during running time (similar to LES2 inlet conditions).
Figure 18 displays contours and profiles of the mean velocity magnitude and figure 19 shows contours and profiles of the turbulent kinetic energy (TKE) at cross sections in the mouth-throat and trachea (stations A-E). Remarkable agreement is observed between the mesh resolutions examined, suggesting mesh convergent results even on the coarse resolution (M1b). Mesh M1a has overall good agreement with the rest of the meshes, however has difficulties in predicting the low speed region at the start of the trachea (just downstream glottis constriction - station D), suggesting that at least 5 elements inside the boundary layer are needed to properly solve that region of the geometry. However, it is remarkable how the coarse mesh M1b gives results with reasonable agreement to those of the fine mesh (M2), showing the capability of low dissipation FEM to remain second order accurate even with very complex geometries. Here the key is the capability of such schemes to preserve the kinetic energy of the convective operator without the need of reducing the accuracy of the scheme like in unstructured FVM (for more information see Lehmkuhl et al. (2019)).
RANS Simulations
The gas flowfield calculations in the airway system were conducted for the steady-state by solving the Reynolds-Averaged Navier-Stokes (RANS) equations in connection with an appropriate turbulence model using the open-source platform OpenFOAM 4.1 (OpenFOAM Foundation, 2013b). For coupling the velocity and pressure fields, the SIMPLE (Semi-Implicit-Method-Of-Pressure-Linked-Equations) algorithm is applied. Hence, the module simpleFOAM is used in order to solve the conservation and momentum equations for a steady-state, incompressible and turbulent flow. For comparison three turbulence models were considered, the standard k-ω SST, the standard k-ε and the RNG k-ε turbulence model.
Computational domain and meshes
The geometry used in the RANS calculations is essentially the same geometry as the one used in the LES case (shown in figure 8).
The meshing process is one of the most important parts in solving the airways system. A mesh with insufficient quality of the computational cells (high mesh non-orthogonality or skewness) can result in numerical diffusion and consequently prediction of the gas phase with significant errors (Jasak, 1996). The geometry of the airways system is extremely complex with several changes of sections, branches, constrictions and expansions. Therefore, it is not possible to generate a hexahedral and structured mesh. The solution found for this problem lies in the use of tetrahedral elements, a configuration being more adaptable to the complexity of the mesh. However, this kind of mesh structure can lead to numerical errors mainly in the boundary layers, e.g. near-wall region, making it necessary to create a layer of prismatic elements close to the wall. Two meshes were generated with different near-wall resolutions. Cross-sectional views of these meshes at five stations are shown in figure 20. In the coarser mesh (Mesh 1), only three layers of prismatic elements were used close to the wall; however the results obtained with such mesh resolution were not satisfactory. This problem was solved by refining the mesh close to the wall. Specifically, the near-wall element was divided three times having the two parts closer to the wall at 25% of the original element thickness and the third one having a thickness of 50%, as can be observed in figure 20(b). Table 5 reports grid characteristics for meshes 1 and 2. Mesh 2 was successfully applied to particle deposition studies (Koullapis et al., 2018) and therefore is also used here for the RANS simulations without further analysis of grid convergence. The focus of this study relates to the influence of turbulence model as well as the applied inlet and outlet boundary conditions.
Solution strategy and boundary conditions — Airflow
The present RANS computations were conducted only with Mesh 2 and for a flow rate of 60 L/min. The gas density and the dynamic viscosity are set to 1.184 kg/m3 and , respectively. In the following the applied inlet/outlet and boundary conditions are described. The outlet boundary conditions for the present case which should closely mimic the experimental situation are based on a zero-gradient strategy (see Table 6). No-slip boundary conditions are used at the pipe walls and a zero pressure is assigned to all outlet boundaries. Wall functions are applied in order to solve the turbulence properties in the near wall region, therefore not demanding extra refinements near the wall for a proper solution. As inlet boundary conditions two cases are considered:
Inlet 1: A mapped boundary condition is applied, where the inlet pipe in front of the oral cavity has a length of 30mm. The mapping of the inlet profile was done over a quite short distance of 20mm. With such an approach a developed inlet flow is obtained without the need of simulating a longer pipe at the entrance of the lung model. This procedure is performed by initially setting an averaged value for the desired property (e.g. velocity, turbulent kinetic energy, etc.) at the inlet and defining a reference plane at a certain downstream distance (i.e. in this case 20 mm from the inlet). Following, the new mapped inlet BC takes the value of the desired property from this offset plane and uses it for the next iteration step.
Inlet 2: For this case the short inlet pipe was extended by a straight pipe with a length of 10 times the inlet diameter. The extended grid had the same cross-sectional structure as the short inlet. At the new inlet boundary, a plug flow inlet with constant values of all properties (e.g. velocity, turbulent kinetic energy, specific dissipation rate and dissipation rate) was specified. Hence, the flow developed over the length of the inlet pipe and then entered the lung model with a more or less developed but symmetric profile. The inlet turbulent kinetic energy was fixed and constant based on 5% turbulence intensity:
The dissipation rate (ε) and specific dissipation rate (ω) at the inlet were determined from using the mixing length l and the inlet diameter :
More information about the boundary conditions used in the calculations, as well as all the wall functions and properties needed in the calculations are extensively detailed in the OpenFOAM user guide. A summary of the operational conditions and the boundary condition setup is shown in Table 6.
Numerical accuracy
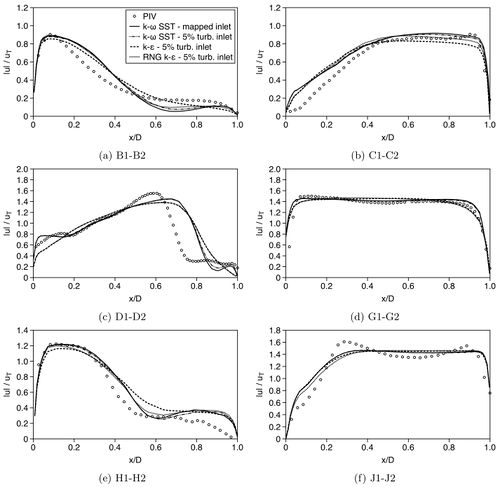
Figure 21 shows comparisons of normalised mean velocity profiles at the locations of the PIV measurement planes IV-VI, between the measurements and RANS computations with different turbulence models and inlet conditions.
The velocity to normalise the simulation results is the bulk velocity of air in the trachea at a flowrate of 60 L/min, .
In general the RANS prediction for the velocity magnitude follow similar trends to the measured data.
However notable deviations exist at stations D, H and J which are located at regions with shear layers, recirculation and flow separation (D is located just downstream the glottis constiction whereas H&J are downstream the first bifurcation in the left and right main bronchi, respectively).
Among the different RANS computations, there are no significant differences.
Only the Inlet 1 condition used with the k-ω SST turbulence model gives slightly lower velocities in the upper region of the oral cavity (figure 21, profile B).
At stations D and H, the simulations with the standard k-ε model yield larger differences in comparison to PIV than those obtained with the RNG k-ε and k-ω SST models.
In conclusion, it is not possible based on the RANS predicted mean velocity profiles to give a preference to a certain turbulence model or the selection of the inlet boundary conditions.
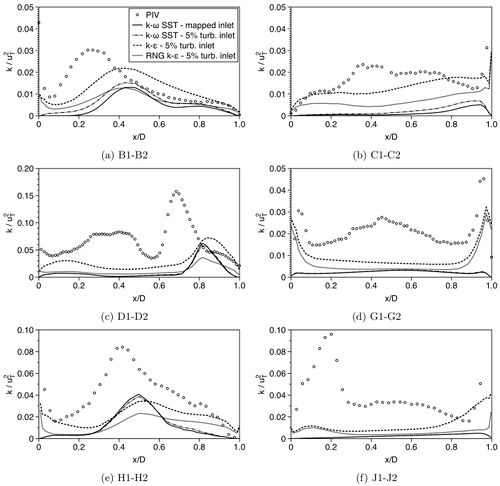
Figure 22 shows comparisons of normalised turbulent kinetic energy profiles at the locations of the PIV measurement planes IV-VI, between the measurements and RANS. All the RANS computations yield much lower turbulent kinetic energy throughout the lung model compared to the measured values. The mapped inlet (Inlet 1) results in extremely low k-values at the first profile B, which is very unrealistic. With the inlet pipe of 10xDinlet (Inlet 2) and an inlet turbulence intensity of 5% the k-ω SST turbulence model yields higher turbulent kinetic energy values. At the rest of stations in the lung model, the k-ω SST turbulence model produces the same turbulence levels no matter which inlet condition was applied. The k-ε models provide overall higher turbulence levels than the k-ω SST model, especially in the near wall regions of the more distal stations (G, H and J). The TKE peaks are associated with near-wall maxima which are also found in some of the measured turbulent kinetic energy profiles. However, the agreement to the measured turbulent kinetic energy levels is still not satisfactory.
Contributed by: P. Koullapisa, J. Muelab, O. Lehmkuhlc, F. Lizald, J. Jedelskyd, M. Jichad, T. Jankee, K. Bauere, M. Sommerfeldf, S. C. Kassinosa —
aDepartment of Mechanical and Manufacturing Engineering, University of Cyprus, Nicosia, Cyprus
bHeat and Mass Transfer Technological Centre, Universitat Politècnica de Catalunya, Terrassa, Spain
cBarcelona Supercomputing center, Barcelona, Spain
dFaculty of Mechanical Engineering, Brno University of Technology, Brno, Czech Republic
eInstitute of Mechanics and Fluid Dynamics, TU Bergakademie Freiberg, Freiberg, Germany
fInstitute Process Engineering, Otto von Guericke University, Halle (Saale), Germany
© copyright ERCOFTAC 2020







![{\displaystyle {\frac {\partial {\overline {u}}_{i}}{\partial t}}+{\overline {u}}_{j}{\frac {\partial {\overline {u}}_{i}}{\partial x_{j}}}=-{\frac {1}{\rho }}{\frac {\partial {\overline {p}}}{\partial x_{i}}}+{\frac {\partial }{\partial x_{j}}}{\bigg [}(\nu +\nu _{sgs}){\frac {\partial {\overline {u}}_{i}}{\partial x_{j}}}{\bigg ]}\qquad (3),}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/281260888a2e360cabd96a3c0cc676664d3ee305)



























