UFR 4-14 References
Flow in pipes with sudden contraction
Underlying Flow Regime 4-14 © copyright ERCOFTAC 2004
References
Astarita, G. and Greco, G. (1968) “Excess pressure drop in laminar flow through sudden contraction”, Ind. Engng Chem. Fundam., Vol. 7 (1), pp. 27-31
Benedict, R.P., Carlucci, N.A., Swetz, S.D. (1966) “Flow losses in abrupt enlargements and contractions”. J. Engineering Power, Vol. 88 (1), pp 73-81
Boger, D. (1982) “Circular entry flows of inelastic and visco-elastic fluids”, Advances in Transport Processes, vol.2
Buckle, U. and Durst, F. (1993) “Investigation of laminar flow in a pipe with sudden contraction of cross sectional area”, Trans. ASME Data for Validation of CFD codes. FED-Vol. 146, pp. 61-78.
Bullen, P.R. and Cheeseman, D.J. (1984) “The definition of pipe contraction pressure loss coefficients for incompressible flow”, Report No. TFAR/1/84, Kingston Polytechnic
Bullen, P.R., Cheeseman, D.J., Hussain, L.A., Ruffell, A.E. (1987) “The determination of pipe contraction pressure loss coefficients for incompressible turbulent flow”, Int. Journal of Heat and Fluid Flow, Vol. 8 (2), pp. 111 – 118
Bullen, P.R., Cheeseman, D.J., Hussain, L.A. (1988) “The effects of inlet sharpness on the pipe contraction pressure loss coefficient”, Int. Journal of Heat and Fluid Flow, Vol. 9 (4), pp.431-433
Bullen, P.R., Hussain, L.A., Cheeseman, D.J. (1990) “Laser Doppler Anemometry measurements of flow through a sudden pipe contraction and comparison with computer predictions”, 3rd International Conf. on Laser Anemometry, Advances and Applications, Springer-Verlag, pp.567-576
Bullen, P.R., Cheeseman, D.J., Hussain, L.A. (1996) “A study of turbulent flow in pipe contractions”, Proc. of IMechE Part E: Journal of Process Mechanical Engineering, Vol. 210 (E3), pp. 171–180
CFX5 Version 5.6 (2003) “CFX5 Solver and Solver Manager Manual”
Christiansen, E.B., Kelsey, S.J., Carter, T.R. (1972) “Laminar tube flow through an abrupt contraction”, American Institute of Chemical Engineers Journal, Vol. 18 (2), pp.372-380
Durst F., and Loy T. (1985) “Investigation of laminar flow in a pipe with sudden contraction of cross sectional area”, Computers & Fluids, Vol. 13(1), pp15-36.
ESDU (2001) “Pressure Losses in flow through a sudden contraction of duct area”, Data Item 01016, ESDU International, London.
Idel’chik, I.E. (1986) “Handbook of hydraulic resistance”, 2nd edition, Hemisphere Publishing Corporation
Jones, W.P. and Launder, B.E. (1973) “Calculation of Low-Reynolds-Number phenomena with a two-equation model of turbulence”, Int. J. of Heat and Mass Transfer, Vol. 16 (6), pp. 1119-1130
Kaye, S.E. and Rosen, S.L. (1971) “The dependence of laminar entrance loss coefficients on contraction ratio for Newtonian fluids”, Am. Inst. Chem. Engrs J., Vol. 17 (5), pp. 1269-1270
Kays, W. M. (1950) “Loss coefficients for abrupt changes in flow cross section with low Reynolds number flow in single and multiple tube systems”, Trans. ASME, Vol. 72, pp. 1067-1074
Kelsey S. (1971) “Isothermal and non-isothermal, laminar, Newtonian and non-Newtonian entrance region flow”. PhD Thesis, University of Utah, Salt Lake City
Levin, L., Clermont, F. (1970) “Etude des pertes de charge singulieres dans les convergents coniques”, Le Genie Civil, T. 147, No.10, pp. 463-470
Menter, F.R. (1994) “Two-equation eddy-viscosity turbulence models for engineering applications”, AIAA Journal, vol. 32 (8), pp. 1598-1605
Miller, D.S. (1971) “Internal flow — a guide to losses in pipe and duct systems”. British Hydromechanics research Association, Cranfield, UK
Sylvester, N. D. and Rosen, S. L. (1970) “Laminar flow in the entrance region of a cylindrical tube: Part I. Newtonian Fluids”, Am. Institute of Chemical Engineers Journal, Vol. 16 (6), pp. 964-966
Vrentas, J.S. and Duda, J.L. (1973) “Flow of a Newtonian fluid through a sudden contraction”, Applied Scientific Research, Vol. 28, pp. 241-260
Wilcox, D.C. (1998) “Turbulence modeling for CFD”, 2nd ed., DCW Industries, Inc., La Canada, CA, pp.103-217.
Zhang, Z. and Kleinstreuer, C. (2003) “Low-Reynolds-Number turbulent flows in locally constricted conduits: a comparison study”, AIAA Journal, Vol. 41 (5), pp. 831-840.
Nomenclature
|
d |
Small tube diameter |
Re |
Reynolds Number |
|
D |
Large tube diameter |
Red |
Small tube outlet Re |
|
K |
Kinetic turbulent energy |
ReD |
Large tube inlet Re |
|
KL |
Pressure loss coefficient |
u |
Axial fluid velocity |
|
l |
Small tube length |
U1 |
Inlet average velocity |
|
L |
Large tube length |
U2 |
Outlet average velocity |
|
Ls1x |
Upstream separation length |
ucl |
Centre-line fluid velocity |
|
Ls1r |
Upstream separation height |
v |
Radial fluid velocity |
|
Ls2x |
Downstream separation length |
x |
Axial distance from contraction plane |
|
Ls2r |
Downstream separation height |
y |
Radial distance |
|
Lx,th |
Throat axial location of downstream sep. |
b |
Contraction ratio (d/D) |
|
p |
Static Pressure |
m |
Fluid dynamic viscosity |
|
ptot |
Total Pressure |
r |
Fluid density |
|
R |
Pipe radius |
s |
Contraction area ratio |
APPENDIX A
Pressure Loss Coefficient
The pressure loss coefficient for a sudden contraction is defined as
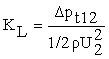
where Δpt12 is the total pressure loss due to the contraction, and 1/2 ρ U22 is the kinetic pressure at Station 2 (see Fig.1). Δpt12 is defined as the total pressure drop between Station 1 in the large pipe and Station 2 in the small pipe minus the losses due to friction for fully developed flow in the large and small pipes extrapolated to the contraction plane. Station 1 and 2 are located in the fully developed regions upstream and downstream of the contraction respectively, outside the region of influence of the contraction. The total pressure loss Δpt12 is derived from measurements of static pressure loss Δp12.
© copyright ERCOFTAC 2004
Contributors: Francesca Iudicello - ESDU