Test Case AC3-08: Difference between revisions
m (Dave.Ellacott moved page SilverP:Test Case AC3-08 to Test Case AC3-08 over redirect) |
|||
| (107 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{AC|front=AC 3-08|description=Description_AC3-08|testdata=Test Case_AC3-08|cfdsimulations=CFD Simulations_AC3-08|evaluation=Evaluation_AC3-08|qualityreview=Quality Review_AC3-08|bestpractice=Best Practice Advice_AC3-08|relatedUFRs=Related UFRs_AC3-08}} | |||
='''Spray evaporation in turbulent flow'''= | ='''Spray evaporation in turbulent flow'''= | ||
| Line 10: | Line 12: | ||
[http://www-mvt.iw.uni-halle.de/english/index.php? | [http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation]. | ||
| Line 16: | Line 18: | ||
|+ align="bottom"|<b>Table 1.</b> Flow conditions for the considered single- | |+ align="bottom"|<b>Table 1.</b> Flow conditions for the considered single- | ||
and two-phase flows | and two-phase flows | ||
!Case | !width="40"|Case | ||
!Diameter nozzle holder | !width="80"|Diameter nozzle holder | ||
!Air volume flow rate | !Air volume flow rate | ||
!Air mass flow rate | !Air mass flow rate | ||
!Maximum air velocity | !Maximum air velocity | ||
!Air temperature | !Air temperature | ||
!Flow Reynolds number | !width="70"|Flow Reynolds number | ||
!Liquid mass flow rate | !Liquid mass flow rate | ||
!Liquid temp. at nozzle exit | !Liquid temp. at nozzle exit | ||
| Line 58: | Line 60: | ||
'''Inlet and Boundary Conditions''' | '''Inlet and Boundary Conditions''' | ||
For all the test cases listed in Table 1, the air flow rate was determined from the integration of the axial velocity profile at the inlet and the associated mass flow rate was determined by multiplication with the air density resulting from the average inlet temperature (i.e. T = 353 K: r = 0.967 kg/ | For all the test cases listed in Table 1, the air flow rate was determined from the integration of the axial velocity profile at the inlet and the associated mass flow rate was determined by multiplication with the air density resulting from the average inlet temperature (i.e. T = 353 K: | ||
r = 0.967 kg/m<sup>3</sup>; T = 373 K: r = 0.915 kg/m<sup>3</sup>). | |||
The liquid flow rate was obtained using a flow meter. The data for all the test cases include profiles of all the components of the gas velocity at the inlet. Profiles of the gas temperature at the air inlet were measured, but it can be assumed to be constant across the annular jet according to the air temperature specified in Table 1. These data are only provided for the single phase flow case. Moreover, Table 1 provides the flow Reynolds number determined with the test section diameter and the air flow properties at the inlet, namely air flow rate, density and dynamic viscosity (i.e. T = 353 K: m = 20.9×10<sup>-6</sup> Ns/m<sup>2</sup>; | |||
T = 373 K: m = 21.7×10<sup>-6</sup> Ns/m<sup>2</sup>). | |||
The droplet phase properties were measured 8 mm downstream of the nozzle exit | |||
(i.e. 3 mm downstream of the edge of the nozzle holder). | |||
The data include profiles of the mean and RMS velocity components, the droplet mass flux, and the characteristic droplet mean diameters. These inlet profiles are obtained over the entire droplet size spectrum. Additionally, droplet size distributions and size-velocity correlations are given for several radial distances. The number averaged droplet diameter at the inlet was about 20 mm for all cases. For specifying appropriate wall boundary conditions also the outer wall temperature along the test section was measured for the single- and two-phase flow | |||
(see: [http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation]). | |||
| Line 64: | Line 73: | ||
All of the liquid and vapour properties and the required correlation for isopropyl alcohol are summarised below. | All of the liquid and vapour properties and the required correlation for isopropyl alcohol are summarised below. | ||
Viscosity: | Viscosity: | ||
| Line 69: | Line 79: | ||
The temperature dependence of the viscosity of the gaseous isopropyl may be obtained by the method of corresponding states. From the VDI-Wärmeatlas Blatt Da 25, one obtains the following equation for the viscosity in [Pa s]: | The temperature dependence of the viscosity of the gaseous isopropyl may be obtained by the method of corresponding states. From the VDI-Wärmeatlas Blatt Da 25, one obtains the following equation for the viscosity in [Pa s]: | ||
<center><math> | |||
\mu = \left[{(\mu\xi)}^{r}f_{p}\right]\frac{1}{\xi} | |||
</math></center> | |||
With the normalised temperature ''T<sub>r</sub>'' = ''T/T<sub>crit</sub>'' | |||
(''T<sub>crit</sub>'' is the critical temperature given at the end of this section), one obtains: | |||
<center><math> | |||
(\mu\xi)^r= {0.807}T_r-{0.357}e^{-{0.449}T_r}+{0.34}e^{-{4.058}T_r}+{0.018} | |||
</math></center> | |||
and the factor <math>\zeta</math> is calculated from: | |||
<center><math> | |||
\xi = \frac{\left[T_{c}/\text{K} \right]^{1/6} \left[R/\text{(J/kmolK)}\right]^{1/6} \left[N_{A}/\text{(l/kmol)}\right]^{1/3}}{\left[M/\text{(kg/kmol)}\right]^{1/2} \left[p_{c}/{(\text{N/m}^2)}\right]^{2/3}} | |||
</math></center> | |||
The constant ''f<sub>p</sub>'' which has to be considered for polar gases is ''f<sub>p</sub>'' = 1.141824 for isopropyl. | |||
Specific heat capacity: | |||
The specific heat capacity [kJ/(kg K)] of isopropyl vapour is calculated according | |||
to the ideal gas assumption (VDI Wärmeatlas, Blatt Da 21) with the equation: | |||
The values of | |||
<center><math> | |||
c^\text{id}_p = \frac{4.1868}{M}\left[\sum\limits_{i} n_{i}A_{i} + \sum\limits_{i} n_{i}B_{i}T + \sum\limits_{i} C_{i}T^2 + \sum\limits_{i} n_{i}D_{i}T^3\right] | |||
</math></center> | |||
The values of ''A<sub>i</sub>'', ''B<sub>i</sub>'', ''C<sub>i</sub>'' and ''D<sub>i</sub>'' | |||
for the individual elements of isopropyl are listed in Table 2. | |||
{|border="1" cell padding="25" cell spacing="3" | {|border="1" cell padding="25" cell spacing="3" align="center" width="350" | ||
|+ align="bottom"|<b>Table 2 Constants for CH<sub>3</sub>, CH and OH; | |||
Isopropyl alcohol: ((CH3)<sub>2</sub> CH OH)</b> | |||
! !! A !! B !! C !! D | ! !! A !! B !! C !! D | ||
|- | |- | ||
|< | |align="center"|CH<sub>3</sub> ||align="center"|0.6087|| align="center"|2.1433 | ||
|align="center"|-0.0852 ||align="center"|0.1135 | |||
|- | |- | ||
|CH || -3.5232 || 3.4158 || -0.2816 || 0.8015 | |align="center"|CH ||align="center"| -3.5232 ||align="center"| 3.4158 | ||
|align="center"|-0.2816 ||align="center"| 0.8015 | |||
|- | |- | ||
|OH || 6.5128 || -0.1347 || 0.0414 || -0.1623 | |align="center"|OH ||align="center"| 6.5128 ||align="center"| -0.1347 | ||
|align="center"|0.0414 ||align="center"| -0.1623 | |||
|} | |} | ||
| Line 114: | Line 142: | ||
The heat capacity of the liquid isopropyl is obtained by (VDI Wärmeatlas, Blatt Da 23): | The heat capacity of the liquid isopropyl is obtained by (VDI Wärmeatlas, Blatt Da 23): | ||
<center> | |||
<math> | |||
c_{p,L} = c^\text{id}_{p} + \Delta c_{p} | |||
</math> | |||
<math>\ | <math> | ||
\frac{\Delta c_{p}}{R_{m}} = 2.56 + 0.436 {(1-T_{r})}^{-1} + \omega \left[2.91 + 4.28 {(1-T_{r})}^{1/3} T^{-1}_{r} + 0.296 {(1-T_{r})}^{-1}\right] | |||
</math> | |||
</center> | |||
with ''ω'' = 0.669 and ''R<sub>m</sub>'' = ''R/M'' being the specific gas constant. | |||
with | |||
The heat capacity of air (mixture of nitrogen and oxygen) was calculated according to Perry (1984): | The heat capacity of air (mixture of nitrogen and oxygen) was calculated according to Perry (1984): | ||
<math> | <center><math> | ||
c_{pair} = 0.79\times c_{p,N_2} + 0.21\times c_{p,O_2} | |||
</math></center> | |||
Thermal conductivity: | Thermal conductivity: | ||
| Line 131: | Line 166: | ||
For isopropyl alcohol, the thermal conductivity in [kW/(m K)] is calculated from: | For isopropyl alcohol, the thermal conductivity in [kW/(m K)] is calculated from: | ||
<math> | <center><math> | ||
\lambda = \frac{\mu}{M}\left(1.3 {c}_{v} + 1.843 R - 1.256 {c}_\text{ir} - \frac{0.347R}{T_{r}} - 3\alpha\right) | |||
</math></center> | |||
with: | with: | ||
''α'' = 1.067 | |||
''c<sub>ir</sub>'' = 4.38 | |||
''c<sub>v</sub>'' = ''c<sub>p</sub>M'' - ''R'' | |||
The thermal conductivity [W/(m K)] for air is obtained from: | The thermal conductivity [W/(m K)] for air is obtained from: | ||
<center><math> | |||
\lambda_\text{air}(T) = \lambda_\text{air}(373K){\left(\frac{T}{373}\right)}^{1.8} | |||
</math></center> | |||
< | with: ''λ<sub>air</sub>''(373 K) = 0.03139 | ||
| Line 155: | Line 193: | ||
The vapour pressure for isopropyl is obtained from the Clausius-Clapeyron relation: | The vapour pressure for isopropyl is obtained from the Clausius-Clapeyron relation: | ||
<math>\ | <center><math> | ||
\ln\frac{P_{s,T}}{P_{s,T\text{ref}}} = \frac{\Delta H_{v}}{R}\left(\frac{1}{T_\text{ref}} - | |||
\frac{1}{T}\right) | |||
</math></center> | |||
where | where ''ΔH<sub>v</sub>'' is the latent heat of vaporisation | ||
at temperature T which may be obtained from: | |||
<math> | <center><math> | ||
\Delta H_{v}{(T)} = \Delta H_{v}{(T_\text{ref})} - | |||
\left(\frac{1-T/T_{c}}{1-T_\text{ref}/T_{c}}\right)^{0.38} | |||
</math></center> | |||
with: | with: ''ΔH<sub>v</sub>''(355) = 666.4 kJ/kg (Perry, 1984). | ||
| Line 172: | Line 217: | ||
The coefficient of binary diffusion for isopropyl in air was measured for different temperatures (e.g. Vargaftik, 1983). The following correlation may be used: | The coefficient of binary diffusion for isopropyl in air was measured for different temperatures (e.g. Vargaftik, 1983). The following correlation may be used: | ||
<math> | <center><math> | ||
D = 4.75\times 10^{-10}\ T^{1.75}_\text{av} [\text{m}^2/\text{s}] | |||
</math></center> | |||
where | where ''T<sub>av</sub>'' is the average temperature in the vapour film around the droplet and may be obtained, for example, by the “1/3” averaging rule. | ||
| Line 183: | Line 230: | ||
Isopropyl: | Isopropyl: | ||
Molar mass M 60.09 kg/kmol | Molar mass ''M ''= 60.09 kg/kmol | ||
''T<sub>crit</sub>'' = 508.3 K | |||
''P<sub>crit</sub>'' = 48.2 bar | |||
''ρ<sub>1</sub>''(liquid) = 785 kg/m<sup>3</sup> | |||
Air: | Air: | ||
Molar mass M 28.84 kg/kmol | Molar mass ''M'' = 28.84 kg/kmol | ||
''T<sub>crit</sub>'' = 132.5 K | |||
''P<sub>crit</sub>'' = 37.7 bar | |||
''ρ''(373 K) = 0.9329kg/m<sup>3</sup> | |||
'''Measurement Errors''' | '''Measurement Errors''' | ||
The air flow rate was determined from the integration of the axial velocity profile at the inlet and the associated mass flow rate was determined by multiplication with the air density resulting from the average inlet temperature. Hence an accuracy of ±10% can be estimated. The liquid flow rate could be adjusted within ±5% by using a flow meter. The velocity measurements of the gas phase were performed by sampling 2,000 signals at each measurement location. Therefore, a high degree of confidence is given. The droplet phase properties were obtained from 20,000 samples over the entire size spectrum ensuring statistical reliable data for the mean properties and the associated rms-values (the mean and rms-values of all velocity components are provided in the database: | The air flow rate was determined from the integration of the axial velocity profile at the inlet and the associated mass flow rate was determined by multiplication with the air density resulting from the average inlet temperature. Hence an accuracy of ±10% can be estimated. The liquid flow rate could be adjusted within ±5% by using a flow meter. The velocity measurements of the gas phase were performed by sampling 2,000 signals at each measurement location. Therefore, a high degree of confidence is given. The droplet phase properties were obtained from 20,000 samples over the entire size spectrum ensuring statistical reliable data for the mean properties and the associated rms-values (the mean and rms-values of all velocity components are provided in the database | ||
[http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation]). This however implies that the statistical reliability for size dependent properties is lower at the edges of the size distributions. The droplet mass flux could be measured with an accuracy of ±10% if the spray was rather symmetric (Sommerfeld & Qiu 1995). | |||
'''Experimental results''' | '''Experimental results''' | ||
Profiles of air or droplet phase properties are available at the cross-section 25, 50, 100, 200, 300 and 400 mm downstream of the inlet. For the single phase flow these are the mean stream-wise and radial velocities and the associated | Profiles of air or droplet phase properties are available at the cross-section 25, 50, 100, 200, 300 and 400 mm downstream of the inlet. For the single phase flow these are the mean stream-wise and radial velocities and the associated RMS-values. Additionally, mean temperature profiles of air were measured at the inlet and within the test section using a thermocouple. In the two-phase flow only the spray droplet properties could be measured, namely the stream-wise and radial droplet mean velocities and rms-values, the droplet mass flux, droplet concentration, and several droplet diameters. Additionally, the droplet mass flow rate along the test section was determined from the integration of the droplet flux profiles. These data are a measure of the integral evaporation rates. | ||
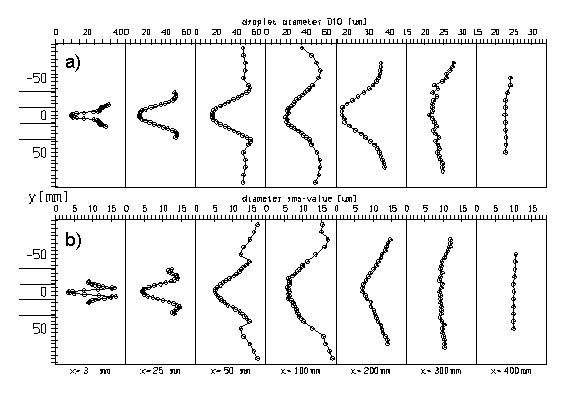
For the spray case 4 the highest evaporation rate within the test section was achieved due to high air temperature and low inlet velocity. The mean stream-wise and radial velocity profiles for this case are presented in Fig. 2. The radial velocity could only be measured over half a cross-section, but clearly indicates the spreading of the spray. The axial mean velocity profiles indicate that the spray flow is rather axi-symmetric and that the droplets are continuously decelerated. The profiles of the droplet mass flux (Fig. 3) also are rather symmetric and of course reveal the rather quick evaporation of the droplets in this case. Initially, the flux profiles have two maximum values associated with a hollow cone spray. Finally, Fig. 4 shows the profiles of the droplet number mean diameter and the associated | For the spray case 4 the highest evaporation rate within the test section was achieved due to high air temperature and low inlet velocity. The mean stream-wise and radial velocity profiles for this case are presented in Fig. 2. The radial velocity could only be measured over half a cross-section, but clearly indicates the spreading of the spray. The axial mean velocity profiles indicate that the spray flow is rather axi-symmetric and that the droplets are continuously decelerated. The profiles of the droplet mass flux (Fig. 3) also are rather symmetric and of course reveal the rather quick evaporation of the droplets in this case. Initially, the flux profiles have two maximum values associated with a hollow cone spray. Finally, Fig. 4 shows the profiles of the droplet number mean diameter and the associated RMS-values. Also these profiles are rather symmetric and exhibit the typical shape with large droplets at the edge of the spray. The rms-value shows that in this region the droplet size distributions are rather wide (see also Sommerfeld & Qiu 1998). | ||
| Line 241: | Line 289: | ||
Site Design and Implementation: [[Atkins]] and [[UniS]] | Site Design and Implementation: [[Atkins]] and [[UniS]] | ||
{{AC|front=AC 3-08|description=Description_AC3-08|testdata=Test Case_AC3-08|cfdsimulations=CFD Simulations_AC3-08|evaluation=Evaluation_AC3-08|qualityreview=Quality Review_AC3-08|bestpractice=Best Practice Advice_AC3-08|relatedUFRs=Related UFRs_AC3-08}} | |||
Latest revision as of 16:08, 11 February 2017
Spray evaporation in turbulent flow
Application Challenge 3-08 © copyright ERCOFTAC 2004
Overview of the Experiments
For allowing a detailed analysis of the different effects on spray evaporation several sets of measurements were performed. The geometry is specified in Fig. 1. Heated air was injected through an annulus with 64 mm outer diameter and the diameter of the nozzle holder was 20 and 40 mm, respectively. The test section had a diameter of 200 mm and the length was 1500 mm. The first flow condition considered in the studies was a single phase flow case (i.e. without the liquid spray being operated, see Table 1) in order to assess the flow characteristics and quality of the established air flow and the effect of the spray and the evaporation on the flow (i.e. two-way coupling). The air velocity profiles were obtained by Laser-Doppler anemometry. For this purpose the flow was seeded with 1.5 mm tracer particles. It should be noted that in the two-phase flow (i.e. with operating spray) the gas phase velocity could not be measured since the probability of droplets with diameters less than 5 mm was extremely low to yield reliable measurements. The two-phase flow (i.e. only the droplet properties were determined) was examined for four flow conditions with different air flow rates, air temperatures, liquid flow rates, and diameters of the nozzle holder (Sommerfeld and Qiu 1998). The main parameters for the different experimental conditions are summarised in Table 1. The droplet phase properties (i.e. droplet size, velocity and mass flux) were measured at several cross-sections downstream of the inlet, namely at 25, 50, 100, 200, 300, and 400 mm. Phase-Doppler anemometry (PDA) was applied to obtain the spatial change of the droplet size spectrum in the flow field and to measure droplet size-velocity correlations. The measurement size range was up to 115 mm with equidistant size classes of 5 mm. A description of the test case, the liquid properties, and the data is also available at:
http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation.
| Case | Diameter nozzle holder | Air volume flow rate | Air mass flow rate | Maximum air velocity | Air temperature | Flow Reynolds number | Liquid mass flow rate | Liquid temp. at nozzle exit |
|---|---|---|---|---|---|---|---|---|
| (mm) | (m3/s) | (g/s) | (m/s) | (°C) | (g/s) | (°C) | ||
| Single phase | 40 | 0.032 | 29.0 | 18.0 | 100 | 8,577 | − | − |
| 1 | 40 | 0.034 | 32.6 | 18.0 | 80 | 10,024 | 0.44 | 32 |
| 2 | 40 | 0.031 | 28.3 | 18.0 | 100 | 8,309 | 0.44 | 34 |
| 3 | 40 | 0.015 | 14.2 | 9.0 | 80 | 4,422 | 0.44 | 32 |
| 4 | 20 | 0.023 | 21.2 | 9.0 | 100 | 6,165 | 0.83 | 34 |
Inlet and Boundary Conditions
For all the test cases listed in Table 1, the air flow rate was determined from the integration of the axial velocity profile at the inlet and the associated mass flow rate was determined by multiplication with the air density resulting from the average inlet temperature (i.e. T = 353 K: r = 0.967 kg/m3; T = 373 K: r = 0.915 kg/m3). The liquid flow rate was obtained using a flow meter. The data for all the test cases include profiles of all the components of the gas velocity at the inlet. Profiles of the gas temperature at the air inlet were measured, but it can be assumed to be constant across the annular jet according to the air temperature specified in Table 1. These data are only provided for the single phase flow case. Moreover, Table 1 provides the flow Reynolds number determined with the test section diameter and the air flow properties at the inlet, namely air flow rate, density and dynamic viscosity (i.e. T = 353 K: m = 20.9×10-6 Ns/m2; T = 373 K: m = 21.7×10-6 Ns/m2). The droplet phase properties were measured 8 mm downstream of the nozzle exit (i.e. 3 mm downstream of the edge of the nozzle holder). The data include profiles of the mean and RMS velocity components, the droplet mass flux, and the characteristic droplet mean diameters. These inlet profiles are obtained over the entire droplet size spectrum. Additionally, droplet size distributions and size-velocity correlations are given for several radial distances. The number averaged droplet diameter at the inlet was about 20 mm for all cases. For specifying appropriate wall boundary conditions also the outer wall temperature along the test section was measured for the single- and two-phase flow (see: http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation).
Thermodynamic Properties of Fluids
All of the liquid and vapour properties and the required correlation for isopropyl alcohol are summarised below.
Viscosity:
The temperature dependence of the viscosity of the gaseous isopropyl may be obtained by the method of corresponding states. From the VDI-Wärmeatlas Blatt Da 25, one obtains the following equation for the viscosity in [Pa s]:
With the normalised temperature Tr = T/Tcrit (Tcrit is the critical temperature given at the end of this section), one obtains:
and the factor is calculated from:
The constant fp which has to be considered for polar gases is fp = 1.141824 for isopropyl.
Specific heat capacity:
The specific heat capacity [kJ/(kg K)] of isopropyl vapour is calculated according to the ideal gas assumption (VDI Wärmeatlas, Blatt Da 21) with the equation:
The values of Ai, Bi, Ci and Di
for the individual elements of isopropyl are listed in Table 2.
| A | B | C | D | |
|---|---|---|---|---|
| CH3 | 0.6087 | 2.1433 | -0.0852 | 0.1135 |
| CH | -3.5232 | 3.4158 | -0.2816 | 0.8015 |
| OH | 6.5128 | -0.1347 | 0.0414 | -0.1623 |
The heat capacity of the liquid isopropyl is obtained by (VDI Wärmeatlas, Blatt Da 23):
with ω = 0.669 and Rm = R/M being the specific gas constant.
The heat capacity of air (mixture of nitrogen and oxygen) was calculated according to Perry (1984):
Thermal conductivity:
For isopropyl alcohol, the thermal conductivity in [kW/(m K)] is calculated from:
with:
α = 1.067
cir = 4.38
cv = cpM - R
The thermal conductivity [W/(m K)] for air is obtained from:
with: λair(373 K) = 0.03139
Vapour pressure:
The vapour pressure for isopropyl is obtained from the Clausius-Clapeyron relation:
where ΔHv is the latent heat of vaporisation
at temperature T which may be obtained from:
with: ΔHv(355) = 666.4 kJ/kg (Perry, 1984).
Coefficient of binary diffusion:
The coefficient of binary diffusion for isopropyl in air was measured for different temperatures (e.g. Vargaftik, 1983). The following correlation may be used:
where Tav is the average temperature in the vapour film around the droplet and may be obtained, for example, by the “1/3” averaging rule.
Additional properties:
Isopropyl:
Molar mass M = 60.09 kg/kmol
Tcrit = 508.3 K
Pcrit = 48.2 bar
ρ1(liquid) = 785 kg/m3
Air:
Molar mass M = 28.84 kg/kmol
Tcrit = 132.5 K
Pcrit = 37.7 bar
ρ(373 K) = 0.9329kg/m3
Measurement Errors
The air flow rate was determined from the integration of the axial velocity profile at the inlet and the associated mass flow rate was determined by multiplication with the air density resulting from the average inlet temperature. Hence an accuracy of ±10% can be estimated. The liquid flow rate could be adjusted within ±5% by using a flow meter. The velocity measurements of the gas phase were performed by sampling 2,000 signals at each measurement location. Therefore, a high degree of confidence is given. The droplet phase properties were obtained from 20,000 samples over the entire size spectrum ensuring statistical reliable data for the mean properties and the associated rms-values (the mean and rms-values of all velocity components are provided in the database http://www-mvt.iw.uni-halle.de/english/index.php?spray_evaporation). This however implies that the statistical reliability for size dependent properties is lower at the edges of the size distributions. The droplet mass flux could be measured with an accuracy of ±10% if the spray was rather symmetric (Sommerfeld & Qiu 1995).
Experimental results
Profiles of air or droplet phase properties are available at the cross-section 25, 50, 100, 200, 300 and 400 mm downstream of the inlet. For the single phase flow these are the mean stream-wise and radial velocities and the associated RMS-values. Additionally, mean temperature profiles of air were measured at the inlet and within the test section using a thermocouple. In the two-phase flow only the spray droplet properties could be measured, namely the stream-wise and radial droplet mean velocities and rms-values, the droplet mass flux, droplet concentration, and several droplet diameters. Additionally, the droplet mass flow rate along the test section was determined from the integration of the droplet flux profiles. These data are a measure of the integral evaporation rates.
For the spray case 4 the highest evaporation rate within the test section was achieved due to high air temperature and low inlet velocity. The mean stream-wise and radial velocity profiles for this case are presented in Fig. 2. The radial velocity could only be measured over half a cross-section, but clearly indicates the spreading of the spray. The axial mean velocity profiles indicate that the spray flow is rather axi-symmetric and that the droplets are continuously decelerated. The profiles of the droplet mass flux (Fig. 3) also are rather symmetric and of course reveal the rather quick evaporation of the droplets in this case. Initially, the flux profiles have two maximum values associated with a hollow cone spray. Finally, Fig. 4 shows the profiles of the droplet number mean diameter and the associated RMS-values. Also these profiles are rather symmetric and exhibit the typical shape with large droplets at the edge of the spray. The rms-value shows that in this region the droplet size distributions are rather wide (see also Sommerfeld & Qiu 1998).
Fig. 2 Profiles of measured axial (a) and radial (b) droplet mean velocities along the test section for case 4
Fig. 3 Profiles of the measured droplet mass flux along the test section for case 4
Fig. 4 Profiles of the droplet number mean diameter (a) and the diameter rms-value (b) along the test section for case 4
© copyright ERCOFTAC 2004
Contributors: Martin Sommerfeld - Martin-Luther-Universitat Halle-Wittenberg
Site Design and Implementation: Atkins and UniS
![{\displaystyle \mu =\left[{(\mu \xi )}^{r}f_{p}\right]{\frac {1}{\xi }}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3e136000e4d4436ce6536832fa858d6ccfe95e67)


![{\displaystyle \xi ={\frac {\left[T_{c}/{\text{K}}\right]^{1/6}\left[R/{\text{(J/kmolK)}}\right]^{1/6}\left[N_{A}/{\text{(l/kmol)}}\right]^{1/3}}{\left[M/{\text{(kg/kmol)}}\right]^{1/2}\left[p_{c}/{({\text{N/m}}^{2})}\right]^{2/3}}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fa86f8920d174bed1b4e16f89ca9fad0a79e67ff)
![{\displaystyle c_{p}^{\text{id}}={\frac {4.1868}{M}}\left[\sum \limits _{i}n_{i}A_{i}+\sum \limits _{i}n_{i}B_{i}T+\sum \limits _{i}C_{i}T^{2}+\sum \limits _{i}n_{i}D_{i}T^{3}\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f411a38c61144e45884299c2b443fb54d8028cf6)

![{\displaystyle {\frac {\Delta c_{p}}{R_{m}}}=2.56+0.436{(1-T_{r})}^{-1}+\omega \left[2.91+4.28{(1-T_{r})}^{1/3}T_{r}^{-1}+0.296{(1-T_{r})}^{-1}\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/87dedd62d52a343c752955d05801c001227d5446)





![{\displaystyle D=4.75\times 10^{-10}\ T_{\text{av}}^{1.75}[{\text{m}}^{2}/{\text{s}}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a60fa07886d49ee4f088e525db601183d7527704)